News Reader.info

ABSTRACT Circular dichroism, that is, the differential absorption of a system to left and right circularly polarized light, is one of the only techniques capable of providing morphological

information of certain samples. In biology, for instance, circular dichroism spectroscopy is widely used to study the structure of proteins. More recently, it has also been used to

characterize metamaterials and plasmonic structures. Typically, circular dichorism can only be observed in chiral objects. Here we present experimental results showing that a non-chiral

sample such as a subwavelength circular nanoaperture can produce giant circular dichroism when a vortex beam is used to excite it. These measurements can be understood by studying the

symmetries of the sample and the total angular momentum that vortex beams carry. Our results show that circular dichroism can provide a wealth of information about the sample when combined

with the control of the total angular momentum of the input field. You have full access to this article via your institution. Download PDF SIMILAR CONTENT BEING VIEWED BY OTHERS NONLINEAR

HELICAL DICHROISM IN CHIRAL AND ACHIRAL MOLECULES Article 28 November 2022 POLARIZATION-DISPERSIVE IMAGING SPECTROMETER FOR SCATTERING CIRCULAR DICHROISM SPECTROSCOPY OF SINGLE CHIRAL

NANOSTRUCTURES Article Open access 18 March 2022 ENANTIO-SENSITIVE UNIDIRECTIONAL LIGHT BENDING Article Open access 24 June 2021 INTRODUCTION Since its discovery in the nineteenthth century,

circular dichroism (CD) has been widely used in science. Defined as the differential absorption of left and right circular polarization (LCP or RCP)1, its uses are as diverse as protein

spectroscopy, DNA studies and characterization of the electronic structure of samples2. In some cases, when the CD signal is too weak, a variation of CD is used in exciting the sample with a

strong magnetic field oriented parallel to the direction of light propagation3,4. This variation, known as magnetic CD, can detect some transitions and paramagnetic phenomena that are too

weak to be seen with conventional CD. In the advent of nanophotonic circuitry, a lot of work has been put recently into characterizing plasmonic components in terms of both techniques, but

especially CD5,6,7,8. Typically, it was thought that samples that produced CD had to be chiral, that is, they could not be superimposed with its mirror image9. However, recent experiments

with planar mirror-symmetric plasmonic structures have shown that a non-zero CD can be obtained if the sample is illuminated at oblique angles10,11,12,13. Other attempts to create CD with a

non-chiral sample have been carried out surrounding the sample with a chiral medium14,15,16. In this article, we show for the first time how to induce CD in a non-chiral sample, under normal

incidence. In contrast to the previous approaches, the mirror symmetry of the system is broken with an internal degree of freedom of the input beam: its angular momentum (AM). The AM of

light has gained a lot of interest since the seminal work of Allen _et al_.17 One of the interesting properties of the AM of light is that photons carry AM in packets of _mℏ_ units.

Furthermore, it was shown that the AM of a beam is linearly related to the rotation speed that absorbing particles can achieve when they interact with the beam18. Our experiments show that

CD can be induced in a non-chiral sample if the two (left and right) circularly polarized modes are vortex beams. The reason behind this interesting phenomenon is that the input beams are

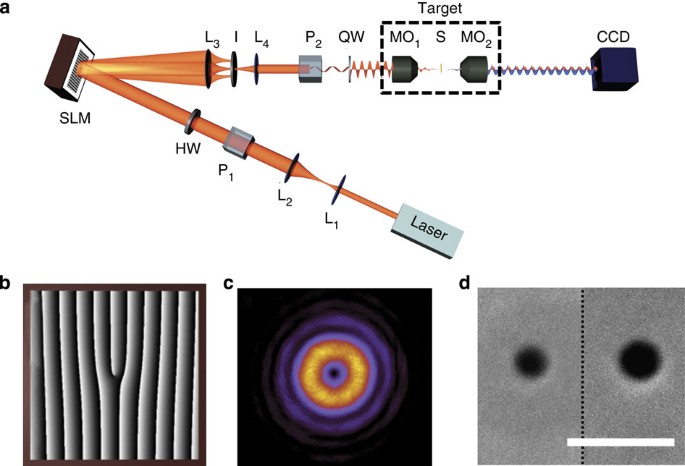
not mirror images of each other. RESULTS EXPERIMENTAL SET-UP A sketch of the experimental set-up we used is depicted in Fig. 1. It can be divided into three parts: preparation of states,

non-paraxial interaction with the sample and measurement. For the state preparation we use a CW laser working at wavelength _λ_0=633 nm, producing a collimated, linearly polarized Gaussian

beam. From this Gaussian beam, we create a vortex beam (see Fig. 1c) with a spatial light modulator (SLM) by displaying an optimized pitchfork hologram19 (see Fig. 1b). Proper control of the

pitchfork hologram allows us to create a phase singularity of order _q_ in the centre of the beam, that is, the phase of the beam twists around its centre from 0 to 2_πq_ radians in one

revolution. Note that when _q_=0, the SLM behaves simply as a mirror. We finish the preparation of the input beam by setting its polarization to either LCP or RCP. This change of

polarization does not appreciably affect the spatial shape of the input beam. After this initial preparation, the light is focused down to interact with a plasmonic sample using a high

numerical aperture (NA=1.1) microscope objective. The samples are circular nano-apertures drilled in a 200-nm gold film deposited on a 1-mm glass substrate (see Fig. 1d). The diameters of

the nano-apertures range from 200 to 450 nm (see Methods). They are centred with respect to the incident beam with a nano-positioning stage. The interaction of the light and the centred

nano-aperture occurs in the non-paraxial regime. Typically, the nano-aperture only allows a small part of the incoming beam to be transmitted. The transmitted light is scattered in all

directions. This facilitates the coupling of light to superficial modes of light, as it has been described theoretically and experimentally by many authors20,21,22. The transmitted light is

then collected by another microscope objective. Finally, a camera is used to capture the transmitted intensity. The CD of our samples is measured using the following procedure: first, we

create a vortex beam of optical charge _q_ with the SLM. Second, we rotate QW to polarize the beam with LCP. Then, we centre the sample with respect to the beam, at the focal plane of MO1.

We measure the transmitted intensity , where _L_ stands for the polarization of the beam (LCP) and _q_ for its optical charge. Then, we rotate QW again to change the polarization state to

RCP and re-centre the sample. At last, we measure the transmitted intensity . From there, the CD associated to the vortex beam with charge _q_ can be obtained in the usual manner: the

transmitted intensity with LCP and RCP modes are subtracted and the result is normalized by their addition: EXPERIMENTAL RESULTS Our results are presented in Table 1 and Fig. 2. The first

column of Table 1 shows the size of the nano-aperture under consideration. The rest of the columns show the measured CD using beams with different phase singularities of order _q_=−1, 0, 1,

respectively. As expected, because of the fact that the circular nano-aperture is mirror-symmetric and the incidence is normal, the CD is very close to zero when the incident beam is

Gaussian (_q_=0). The residual CD can be attributed to small asymmetries on the sample or the incoming beam. When vortex beams with _q_=−1, 1 are used, the situation is very different. We

obtain a very large value for the CD, of the order of 90% for some nano-apertures, even though the incidence is normal and the nano-aperture is still mirror-symmetric. Furthermore, it can be

observed that there is an underlying symmetry relating the value of CD1 and CD−1. Indeed, CD1≃CD−1. DISCUSSION Let us now discuss the results presented in Table 1 and Fig. 2. In order to

understand the appearance of CD in a circular sample under normal incidence, we have to take a careful look at the symmetries of the system and the light probing the samples. We can start

considering the symmetries of the target T comprising the two microscope objectives MO1, MO2 and the sample S (see Fig. 1a). This will simplify the discussion, as we will just consider the

interaction of a paraxial beam with T, as well as the output beams that will also be paraxial. Then, as both the circular nano-aperture and the microscope objectives have cylindrical

symmetry along an axis normal to them, T is cylindrically symmetric. Without loss of generality we will label the symmetry axis as _z_ and we will denote the rotations around this axis by

_R__z_. Furthermore, T is also symmetric under any mirror transformation that contains the _z_ axis, for example, a transformation flipping the _x_ axis and leaving the other axes invariant.

We will refer to such transformations as . Now we will turn our attention to the symmetries of the light beams. The electric field of the light beam incident on T can be described within

the paraxial approximation with the complex vector: where , and being the horizontal and vertical polarization vectors, respectively, _A_ is a normalization constant, |K0|=2_π/λ_0 with _λ_0

the wavelength in consideration and _ρ_, _φ_, _z_ are the cylindrical coordinates. An implicit harmonic exp(−_i_2_πct_/_λ_0) dependence is assumed, where _c_ is the speed of light. Note that

_p_=1 refers to LCP and _p_=−1 to RCP. Now, if we apply a rotation around the _z_ axis by an angle _θ_ to this beam, the resulting beam acquires a constant phase: . These kinds of beams are

then eigenstates of the generator of rotations around the _z_ axis, that is, the _z_ component of the total AM _J__z_: . The _J__z_ eigenvalue is _m_=_p_+_q_. In addition, note that a beam

with _p_=0 would be linearly polarized and will be no longer an eigenstate of _J__z_, since a rotation of the field would not leave it invariant. Within the paraxial approximation, the beams

with _p_=±1 are also eigenstates of the helicity operator Λ (refs 23, 24, 25). That is, , where Λ=J·P/|P| and P is the linear momentum operator. Hence, with our notation, a beam with _p_=1

is both LCP and also an eigenvector of Λ with value 1, whereas a beam with _p_=−1 is RCP and its helicity equals to −1. We would like to emphasize that this simple relation between helicity

and polarization is only valid because, as mentioned previously, we are describing the system in the paraxial regime26. When the paraxial approximation does not hold, the polarization of the

field and helicity can no longer be so simply related24. Now, if we apply a mirror transformation to the incident beam we obtain: where _α_ is a phase given by the specific mirror

transformation chosen. That is, we obtain a beam with the AM and the helicity eigenvalues flipped. This is a consequence of the fact that both _J__z_ and Λ anticommute with the mirror

symmetry transformations (ref. 27): and . We will now explain our experimental results. We will start by classifying the transmitted electric field with the parameters _p_ and _q_ from the

incident field: _p_=−1, 1 and _q_=−1, 0, 1. Remember that for the incident field , _p_ is modified with QW and _q_ with the SLM (see Fig. 1). Mathematically, the field can be obtained

through the use of a linear operator, , which can be found using the Green dyadic formalism and contains all the relevant information about target T (refs 21, 28). That is, , where the

action of on the incident field will in general be in the form of a convolution. As is simply the mathematical description of T, inherits the symmetries of T. Thus, because of the

cylindrical and mirror symmetries of the target and given an incident field , the following statements hold: first, the transmitted field will also be an eigenstate of _J__z_ with the same

eigenvalue of _m_=_p_+_q_ (see Methods). Second, two incident beams that are mirror images of each other will produce two transmitted fields that will be mirror images (see Methods). That

is, given two mirror-symmetric beams such as and (see equation (3)), their transmitted beams and will be connected via a mirror symmetry: . The proof can be found in Methods, but the

physical idea is the following one: the invariance of the system under mirror transformations links the output of mirror-inverted inputs. This last result is the key point to understand our

CD measurements with vortex beams presented in Table 1 and Fig. 2. In equation (1), the intensities can be obtained from the transmitted electric field: where the integral is taken on the

plane of the detector (in our case CCD chip of the camera). Then, for a mirror-symmetric sample, it can be proven (see Methods) that Let us apply it to prove that _CD_0=0 and that

_CD__q_=−_CD_−_q_. When _q_=0, we obtain that . Substituting this in the definition of CD, equation (1) gives us _CD_0=0. However, when _q_≠0, equation (5) leads us to , which implies that

CD_q_=−CD−_q_, in very good agreement with our measurements. Powerful as these symmetry considerations are, they still cannot explain the quantitative results of CD we obtained, nor their

variation with the diameter of the nano-aperture. Note that, in our experiments, the vortex-induced CD1 varies greatly for different aperture sizes. Thus, holes ~220 nm have a CD close to

90%, while those with sizes ~320 nm present a much lower CD ~10%. Interestingly, the trend is not monotonous and CD1 increases again to 22% for nano-apertures of 430 nm. The symmetry

arguments only indicate that when _q_≠0 the two opposite circular polarizations are not the mirror images of each other and then the associated CD_q_ does not have to be zero. Here the AM of

light plays a crucial role again. In general, it can be observed that CD measurements compare the differential ratio of electromagnetic fields with opposite circular polarization and a

difference of AM of 2 units. For example, CD_q_=1 relates and , whose respective AM values are _m__p_=1=1+1=2 and _m__p_=−1=1−1=0. It is then interesting to observe that CD can also be

sensitive to differential absorption of AM states. In the case of the nano-aperture, this is the most probable cause of the giant value of CD obtained in the experiments. Even though the

sample is cylindrically symmetric, thus preserving the AM of field, input beams with different values of AM have very different scattering amplitudes. This is very similar to what happens in

the scattering from spherical objects, where different spherical modes (the so-called multipolar modes) are scattered with different amplitudes (the Mie coefficients). This problem can be

analytically studied using the Generalized Lorenz-Mie Theory29,30. Using the model of the aplanatic lens31,32 one can check that the fields at the focal plane of MO1 produced by and are very

different (see Fig. 3b). Consequently, their multipolar decompositions33,34 are different as well. These two dissimilar focused fields couple very differently to the multipolar moments of

the structure. In the case of a spherical object, the coupling of multipolar modes depends drastically on its diameter. Furthermore, the relation between the coupling coefficient and the

sphere radius is non-linear and rather complex34, giving rise to the so-called Mie resonances in the scattering of the sphere. Then, given two spheres of different sizes, different coupling

scenarios can occur not only depending on the geometry of the particles but also on the beams used to excite these particles. In fact, similar effects have been experimentally observed for

other plasmonic structures35,36,37. Now, the fact that CD1 increases from 10 to 25% clearly indicates that the nano-apertures are in this multipolar regime34,38. If the experiment was

conducted with larger apertures (non-subwavelength), the result of the CD measurement would monotonously tend towards 0. Indeed, as the size of the scatterer is increased with respect to the

wavelength, the problem can be described with diffraction theory, where the polarization of light does not play any role. In addition, the beams would have to be less focused to interact

with the aperture, otherwise they would just go through it. That would make their intensity and phase profiles much more alike, as shown in Fig. 3b. Last but not the least, notice that the

sign of CD is positive for _q_=1, and negative for _q_=−1. That is, it appears that the transmission of modes with |_J__z_|=2 is larger than the transmission of modes with |_J__z_|=0,

regardless of their helicity content. Now, looking at the intensity distribution of these modes at the focal plane, this result seems counter-intuitive. Figure 3b shows the intensity

distribution of a mode with |_J__z_|=2 (left) and a mode with |_J__z_|=0 (right). One could argue that the mode with |_J__z_|=2 should transmit more intensity through the nano-aperture as

the intensity of its _z_ component is non-null in the centre. Certainly, this effect has been largely studied in STED microscopy. It is known that a non-null _z_ intensity component in the

centre has a detrimental effect for the resolution of the technique39,40. Nevertheless, when using core–shell nanoparticles to enhance the resolution of STED the same conclusion cannot be

drawn41,42. More importantly, Kindler _et al_.43 showed that radial and azimuthally polarized beams have different transmissions through a nanohole. In particular, in this work it is shown

that an azimuthally polarized beam (which has null intensity in the centre) can have a higher transmission than the radially polarized beam (which has a strong _z_ component with a non-null

intensity in the centre) for nanoholes in the range that we probed. In conclusion, we have observed a giant CD on a subwavelength circular aperture induced by vortex beams. We studied the

transmission of beams with three different phase singularities of order _q_=−1, 0, 1. Higher |_q_| have not been used as the cylindrical symmetry of the beam is experimentally broken when

they are focused44,45. We have seen that the results can be elucidated from a symmetry perspective. In particular, we have proved that, even for mirror-symmetric systems, CD can be induced

if the LCP and RCP beams are not connected via a mirror symmetry. Similar results could have been obtained for our samples had we measured an ‘orbital’ dichroism, defined as , that is

inverting the azimuthal phase of the paraxial mode, instead of its polarization. Indeed, using equation (5), it can be proven that and for mirror-symmetric samples. This fact reinforces the

point that CD measurements are sensitive to the differential absorption of AM states. That is, we show that the information carried by CD measurements has two different contributions: the

differential scattering of different circular polarization states but also the differential scattering of different AM states. Notice that equation (5) and the relations between and CD_q_

above will no longer be valid if the sample in use is chiral. A chiral sample interacts differently with the two orthogonal circular polarizations; therefore, the absorption of and will

yield different results. A work along these lines was presented by Löffler _et al_.46 Thus, we expect that vortex beam-induced CD will be able to unveil properties of non-chiral samples that

are hidden to the standard CD measurements. Finally, it is interesting to see that in other related phenomena, such as molecular optical activity, the interplay between the two symmetries

associated to helicity and AM (electromagnetic duality and rotational symmetry) are also essential to fully understand the problem from first principles47. METHODS PRESERVATION OF _J__Z_ FOR

THE TRANSMITTED FIELD We consider the rotation transformations (_R__z_), mirror transformations () and AM (_J__z_) operators, as well as the scattering operator () as linear

integrodifferential operators acting on the electric vector of the complex electromagnetic field. Owing to the invariance of T under rotations around the _z_ axis, the linear operator ,

which contains all the information about the system, commutes with the rotations _R__z_: . Owing to the bijective properties of the exponential function, the same commutation relation holds

for the generator of rotations, _J__z_: . Then, given that is an eigenvector of _J__z_, must also be an eigenvector of _J__z_ with the same eigenvalue: SCATTERING OF MIRROR-SYMMETRIC BEAMS

Owing to the invariance of T under mirror symmetries, the linear operator , which contains all the information about the system, commutes with : . Now, given two mirror-symmetric beams such

as and (see equation (3)), it can be checked that their respective transmitted fields ( and ) are related with a mirror symmetry: PROOF OF As mentioned in the body of the manuscript, the

target is cylindrically symmetric scatterer. Hence, if the incident field is an eigenstate of _J__z_ with eigenvalue (_p_+_q_), then the transmitted field needs to remain an eigenstate of

_J__z_ with the same eigenvalue (_p_+_q_). Nevertheless, the helicity is, in general, not preserved in the interaction. This phenomenon is a consequence of the duality symmetry being highly

broken by the nano-aperture and the multilayer system24,25,48,49. Because duality symmetry is highly broken by the sample, the helicity of the incident beam is not preserved. Thus, the field

comprises two helicity components, one of polarization and another one of polarization : where and are the complex amplitudes of the two polarizations at the plane of the camera. We call

the direct component, as it maintains the polarization state . The other orthogonal component is , and we call it crossed component. The crossed component has a polarization state when the

incident state is . Now, we can use the definition of on equation (4), the decomposition of in its two orthogonal components given by equation (8), and the fact that to obtain that can be

expressed as: Following an identical procedure, the following equation yields for : Choosing the mirror-symmetric operator to be , we can use equation (3) to get a relation between the

coefficients in equations (9 and 10): which implies that and because of the orthogonality of and . Consequently, it follows that: as the integrations limits remain the same under the change

. FABRICATION OF SAMPLES The tested nanoholes were fabricated by milling with a focused ion beam (FIB) on a gold layer of 200 nm, deposited on top of a 1-mm-thick glass substrate. The

distance between them is 50 μm, thus avoiding the coupling of surface plasmons launched from one nanohole to the closest neighbour. IMAGING OF THE SAMPLES The images were taken with a

secondary electron scanning electron microscope (JEOL JSM-6480) operated at 10 keV. The images were analysed with Matlab where the boundaries of the nanoholes were determined by selecting

the pixels whose intensity was below the 10% of the maximum. The presented images on Fig. 1 were not post-processed. The obtained diameters are listed in Table 1 on the manuscript.

NANO-POSITIONING SYSTEM The sample is mounted on a piezo electric transducer on closed-loop with resolution below 0.5 nm (translation range 300 μm with 20-bit USB interface and noise floor

of tens of picometers). ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Zambrana-Puyalto, X. _et al_. Angular momentum-induced circular dichroism in non-chiral nanostructures. _Nat.

Commun._ 5:4922 doi: 10.1038/ncomms5922 (2014). REFERENCES * Barron, L. D. _Molecular Light Scattering and Optical Activity_ Cambridge University Press (2004). * Kelly, S., Jess, T. J. &

Price, N. C. How to study proteins by circular dichroism. _Biochim. Biophys. Acta_ 1751, 119–139 (2005). Article  CAS  PubMed  Google Scholar  * Stephens, P. J. Magnetic circular dichroism.

_Annu. Rev. Phys. Chem._ 25, 201–232 (1974). Article  ADS  CAS  Google Scholar  * Manson, W. R. _Magnetic Circular Dichroism Spectroscopy_ John Wiley & Sons (2007). * Decker, M., Klein,

M. W., Wegener, M. & Linden, S. Circular dichroism of planar chiral magnetic metamaterials. _Opt. Lett._ 32, 856–858 (2007). Article  ADS  CAS  Google Scholar  * Rusz, J. et al.

Influence of plural scattering on the quantitative determination of spin and orbital moments in electron magnetic chiral dichroism measurements. _Phys. Rev. B_ 83, 132402 (2011). Article 

ADS  Google Scholar  * Hendry, E., Mikhaylovskiy, R. V., Barron, L. D., Kadodwala, M. & Davis, T. J. Chiral electromagnetic fields generated by arrays of nanoslits. _Nano Lett._ 12,

3640–3644 (2012). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Sersic, I., van de Haar, M. A., Arango, F. B. & Koenderink, A. F. Ubiquity of Optical activity in planar

metamaterial scatterers. _Phys. Rev. Lett._ 108, 223903 (2012). Article  ADS  PubMed  Google Scholar  * Bishop, D. M. _Group Theory and Chemistry_ Courier Dover Publications (2012). * Plum,

E. et al. Metamaterials: optical activity without chirality. _Phys. Rev. Lett._ 102, 113902 (2009). Article  ADS  CAS  Google Scholar  * Cao, T. & Cryan, M. J. Enhancement of circular

dichroism by a planar non-chiral magnetic metamaterial. _J. Opt._ 14, 085101 (2012). Article  ADS  Google Scholar  * Maoz, B. M., Moshe, A. B., Vestler, D., Bar-Elli, O. & Markovich, G.

Chiroptical effects in planar achiral plasmonic oriented nanohole arrays. _Nano Lett._ 12, 2357–2361 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Ren, M., Plum, E., Xu, J. &

Zheludev, N. I. Giant nonlinear optical activity in a plasmonic metamaterial. _Nat. Commun._ 3, 833 (2012). Article  ADS  PubMed  Google Scholar  * Abdulrahman, N. A. et al. Induced

chirality through electromagnetic coupling between chiral molecular layers and plasmonic nanostructures. _Nano Lett._ 12, 977–983 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Vidal,

X. et al. Coupled plasmons induce broadband circular dichroism in patternable films of silver nanoparticles with chiral ligands. _Nanoscale_ 5, 10550–10555 (2013). Article  ADS  CAS  PubMed

  Google Scholar  * García-Etxarri, A. & Dionne, J. A. Surface-enhanced circular dichroism spectroscopy mediated by nonchiral nanoantennas. _Phys. Rev. B_ 87, 235409 (2013). Article  ADS

  Google Scholar  * Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of laguerre-gaussian laser modes. _Phys.

Rev. A_ 45, 8185–8189 (1992). Article  ADS  CAS  PubMed  Google Scholar  * Friese, M. E. J., Enger, J., Rubinsztein-Dunlop, H. & Heckenberg, N. R. Optical angular-momentum transfer to

trapped absorbing particles. _Phys. Rev. A_ 54, 1593–1596 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Bowman, R. et al. Optimisation of a low cost SLM for diffraction efficiency and

ghost order suppression. _Eur. Phys. J. Spec. Top._ 199, 149–158 (2011). Article  Google Scholar  * Carretero-Palacios., S. _Mechanisms for Enhancing the Optical Transmission through a

Single Subwavelength Hole_ Universidad de Zaragoza (2011). * Fernandez-Corbaton, I., Tischler, N. & Molina-Terriza, G. Scattering in multilayered structures: diffraction from a nanohole.

_Phys. Rev. A_ 84, 053821 (2011). Article  ADS  Google Scholar  * Yi, J.-M. et al. Diffraction regimes of single holes. _Phys. Rev. Lett._ 109, 023901 (2012). Article  ADS  PubMed  Google

Scholar  * Tung, W.-K. _Group Theory in Physics_ World Scientific (1985). * Fernandez-Corbaton, I., Zambrana-Puyalto, X. & Molina-Terriza, G. Helicity and angular momentum: a

symmetry-based framework for the study of light-matter interactions. _Phys. Rev. A_ 86, 042103 (2012). Article  ADS  Google Scholar  * Fernandez-Corbaton, I. et al. Electromagnetic duality

symmetry and helicity conservation for the macroscopic maxwell's equations. _Phys. Rev. Lett._ 111, 060401 (2013). Article  ADS  PubMed  Google Scholar  * Tischler, N. et al.

Experimental control of optical helicity in nanophotonics. _Light Sci. Appl._ 3, e183 (2014). Article  CAS  Google Scholar  * Messiah, A. _Quantum Mechanics_ Dover (1999). * Martin, O. J. F.

& Piller, N. B. Electromagnetic scattering in polarizable backgrounds. _Phys. Rev. E_ 58, 3909–3915 (1998). Article  ADS  CAS  Google Scholar  * Bohren, C. F. & Huffman, D. R.

_Absorption and Scattering of Light by Small Particles_ Wiley (1983). * Gouesbet, G. & Gréhan, G. _Generalized Lorenz-Mie Theories_ Springer (2011). * Richards, R. & Wolf, E.

Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. _Proc. R. Soc. A_ 253, 358–379 (1959). ADS  MATH  Google Scholar  * Novotny, L. &

Hecht, B. _Principles of Nano-Optics_ Cambridge University Press (2006). * Molina-Terriza, G. Determination of the total angular momentum of a paraxial beam. _Phys. Rev. A_ 78, 053819

(2008). Article  ADS  Google Scholar  * Zambrana-Puyalto, X., Vidal, X. & Molina-Terriza, G. Excitation of single multipolar modes with engineered cylindrically symmetric fields. _Opt.

Express_ 20, 24536–24544 (2012). Article  ADS  PubMed  Google Scholar  * Gorodetski, Y., Niv, A., Kleiner, V. & Hasman, E. Observation of the spin-based plasmonic effect in nanoscale

structures. _Phys. Rev. Lett._ 101, 043903 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Banzer, P., Peschel, U., Quabis, S. & Leuchs, G. On the experimental investigation of the

electric and magnetic response of a single nano-structure. _Opt. Express_ 18, 10905–10923 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Rodríguez-Herrera, O. G., Lara, D., Bliokh, K.

Y., Ostrovskaya, E. A. & Dainty, C. Optical nanoprobing via spin-orbit interaction of light. _Phys. Rev. Lett._ 104, 253601 (2010). Article  ADS  PubMed  Google Scholar  * Hancu, I. M.,

Curto, A. G., Castro-López, M., Kuttge, M. & van Hulst, N. F. Multipolar interference for directed light emission. _Nano Lett._ 14, 166–171 (2014). Article  ADS  CAS  PubMed  Google

Scholar  * Hao, X., Kuang, C., Wuang, T. & Liu, X. Effects of polarization on the de-excitation dark focal spot in STED microscopy. _J. Opt._ 12, 115707 (2010). Article  ADS  Google

Scholar  * Khonina, S. N. & Golub, I. How low can STED go? Comparison of different write-erase beam combinations for stimulated emission depletion microscopy. _J. Opt. Soc. Am. A_ 29,

2242–2246 (2012). Article  ADS  Google Scholar  * Foreman, M., Sivan, Y., Maier, S. A. & Török, P. Independence of plasmonic near-field enhancements to illumination beam profile. _Phys.

Rev. B_ 86, 155441 (2012). Article  ADS  Google Scholar  * Sivan, Y., Sonnefraud, Y., Kéna-Cohen, S., Pendry, J. B. & Maier, S. A. Nanoparticle-assisted stimulated-emission-depletion

nanoscopy. _ACS Nano_ 6, 5291–5296 (2012). Article  CAS  PubMed  Google Scholar  * Kindler, J., Banzer, P., Quabis, S., Peschel, U. & Leuchs, G. Waveguide properties of single

subwavelength holes demonstrated with radially and azimuthally polarized light. _Appl. Phys. B_ 89, 517–520 (2007). Article  ADS  CAS  Google Scholar  * Ricci, F., Löffler, W. & van

Exter, M. P. Instability of higher-order optical vortices analyzed with a multi-pinhole interferometer. _Opt. Express_ 20, 22961–22975 (2012). Article  ADS  CAS  PubMed  Google Scholar  *

Neo, R. et al. Correcting vortex splitting in higher order vortex beams. _Opt. Express_ 22, 9920–9931 (2014). Article  ADS  PubMed  Google Scholar  * Löffler, W., Broer, D. J. &

Woerdman, J. P. Circular dichroism of cholesteric polymers and the orbital angular momentum of light. _Phys. Rev. A_ 83, 065801 (2011). Article  ADS  Google Scholar  * Fernandez-Corbaton,

I., Vidal, X., Tischler, N. & Molina-Terriza, G. Necessary symmetry conditions for the rotation of light. _J. Chem. Phys._ 138, 214311 (2013). Article  ADS  PubMed  Google Scholar  *

Zambrana-Puyalto, X., Vidal, X., Juan, M. L. & Molina-Terriza., G. Dual and anti-dual modes in dielectric spheres. _Opt. Express_ 21, 17520–17530 (2013). Article  ADS  PubMed  Google

Scholar  * Bliokh, K. Y., Bekshaev, A. Y. & Nori, F. Dual electromagnetism: helicity, spin, momentum and angular momentum. _New J. Phys._ 15, 033026 (2013). Article  ADS  Google Scholar

  Download references ACKNOWLEDGEMENTS We want to thank Mathieu L. Juan for helpful advice while setting up the experiment and Alexander E. Minovich for the preparation of the sample. The

sample was prepared at the ACT Node of the Australian Nanofabrication Facility, and the scanning electron microscopy images were taken at the Microscopy Unit of Faculty of Science in

Macquarie University. This work was funded by the Australian Research Council Discovery Project DP110103697 and the Centre of Excellence in Engineered Quantum Systems (EQuS). G.M.-T. is the

recipient of an Australian Research Council Future Fellowship (project number FT110100924). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics and Astronomy, Macquarie

University, 2109, New South Wales, Australia Xavier Zambrana-Puyalto, Xavier Vidal & Gabriel Molina-Terriza * ARC Centre for Engineered Quantum Systems, Macquarie University, 2109, New

South Wales, Australia Xavier Zambrana-Puyalto & Gabriel Molina-Terriza Authors * Xavier Zambrana-Puyalto View author publications You can also search for this author inPubMed Google

Scholar * Xavier Vidal View author publications You can also search for this author inPubMed Google Scholar * Gabriel Molina-Terriza View author publications You can also search for this

author inPubMed Google Scholar CONTRIBUTIONS X.Z.-P. and X.V. set up the experiment and did the measurements. X.Z.-P. and G.M.-T. wrote the manuscript. G.M.-T. supervised the project. All

the authors participated in the analysis of the results. CORRESPONDING AUTHOR Correspondence to Gabriel Molina-Terriza. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no

competing financial interests. RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zambrana-Puyalto, X., Vidal, X. & Molina-Terriza, G. Angular

momentum-induced circular dichroism in non-chiral nanostructures. _Nat Commun_ 5, 4922 (2014). https://doi.org/10.1038/ncomms5922 Download citation * Received: 05 March 2014 * Accepted: 06

August 2014 * Published: 12 September 2014 * DOI: https://doi.org/10.1038/ncomms5922 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative