News Reader.info

ABSTRACT Large-scale, highly integrated and low-power-consuming hardware is becoming progressively more important for realizing optical neural networks (ONNs) capable of advanced optical

computing. Traditional experimental implementations need _N__2_ units such as Mach-Zehnder interferometers (MZIs) for an input dimension _N_ to realize typical computing operations

(convolutions and matrix multiplication), resulting in limited scalability and consuming excessive power. Here, we propose the integrated diffractive optical network for implementing

parallel Fourier transforms, convolution operations and application-specific optical computing using two ultracompact diffractive cells (Fourier transform operation) and only _N_ MZIs. The

footprint and energy consumption scales linearly with the input data dimension, instead of the quadratic scaling in the traditional ONN framework. A ~10-fold reduction in both footprint and

energy consumption, as well as equal high accuracy with previous MZI-based ONNs was experimentally achieved for computations performed on the _MNIST_ and _Fashion-MNIST_ datasets. The

integrated diffractive optical network (IDNN) chip demonstrates a promising avenue towards scalable and low-power-consumption optical computational chips for optical-artificial-intelligence.

SIMILAR CONTENT BEING VIEWED BY OTHERS OPTICAL NEURAL NETWORKS: PROGRESS AND CHALLENGES Article Open access 20 September 2024 COMPACT OPTICAL CONVOLUTION PROCESSING UNIT BASED ON MULTIMODE

INTERFERENCE Article Open access 24 May 2023 LARGE-SCALE NEUROMORPHIC OPTOELECTRONIC COMPUTING WITH A RECONFIGURABLE DIFFRACTIVE PROCESSING UNIT Article 12 April 2021 INTRODUCTION Optical

neural networks (ONNs) that exploit photonic hardware acceleration to compute complex matrix-vector multiplication, have the advantages of ultra-high bandwidth, high calculation speed, and

high parallelism over electronic counterparts1,2. With the rapidly increasing complexity in data manipulation techniques and dataset size, highly integrated and scalable ONN hardware with

ultracompact size and the reduced energy consumption is strongly desired to conquer the resource bottleneck in artificial neural networks. Due to the advantages of ultracompact size,

high-density integration, and power-efficiency silicon photonic integrated circuits (PICs) are emerging as a promising candidate for establishing large and compact computing units

predominantly required in optical-artificial-intelligence computers3,4,5. Moreover, the fabrication of silicon PICs is compatible with CMOS technology, thus current infrastructure can

support mass production at a low cost6. Typical silicon PIC architectures to realize chip-scale ONNs7,8,9,10,11,12,13,14,15 use cascades of multiple Mach–Zehnder interferometers

(MZIs)7,8,9,10,11,12,13 and microring resonator-based wavelength division multiplexing technology14,15. Though PICs have shown great potential in integrated optics, the space utilization

(directional couplers and phase modulators)16, energy consumption (heaters to control phase), and the complex control circuits for reducing fluctuation of the resonance wavelength17,18

restrict the development of a large-scale programmable photonic neural network. Additionally, phase-change materials such as Ge2Sb2Te55, inverse-designed metastructures19, and nanoscale

neural medium20 combined with CMOS-compatible integrated photonic platform, can further minimize the size of integrated photonic circuits. However, the number of units for these ONN

architectures scales quadratically with the input data dimension5,7,14 for both convolution operations and matrix multiplication, leading to quadratic scaling in the footprint and energy

consumption. Meanwhile, Fourier transforms and convolutions, which are the fundamental building blocks of ONN architectures, have been realized using various approaches including the spatial

light modulators21,22,23,24, micro-lens array25,26,27,28, and holographic elements29,30,31,32,33. Fourier transforms and convolutions as well as applications in classification tasks have

been proposed utilizing the optical diffraction masks in free space26,31. However, these free-space approaches require heavy auxiliary or modulation equipment which is space-consuming34,35

and exceedingly challenging to program in real-time31,36,37, hindering their feasibilities towards the large-scale implementation and commercialization of photonic neural networks. Here, we

demonstrate the first scalable integrated diffractive neural network (IDNN) chip using silicon PICs, which is capable of performing the parallel Fourier transform and convolution operations.

Due to the utilization of on-chip compact diffractive cells (slab waveguides), both the footprint and power consumption of the proposed architecture is reduced from quadratic scaling in the

input data dimensions required for MZI-based ONN architectures7,10,13 to linear scaling for the IDNN. This reduction in the resource scaling from quadratic to linear will have a profound

impact on the realization of large-scale silicon-photonics computing circuits with current fabrication technologies38,39,40. The parallel Fourier transform and convolution operations in our

IDNN chip can be applied to classification tasks with Iris flower, Handwriting digit, and Fashion product datasets. The cases of 1D sequence and 2D digit image recognition demonstrate the

enhanced performance of the convolution operations. Two typical cases of Iris flower classification with a one-layer neural network, and Handwriting digit and Fashion product classification

with a two-layer neural network as well as the comparison with the fully connected neural network, are conducted to further characterize the classification performance of our IDNN chip. For

the _Iris_ dataset classification, we obtain a chip testing accuracy of 98.3% in the one-layer IDNN using a complex modulation. For Handwriting and Fashion recognition tasks using 500

different sample inputs, the testing accuracies of 89.3 and 81.3% are obtained, respectively, which are equivalent to those obtained in a fully connected neural network. Compared to the

previous design with an area of 5 mm2 and power of 3–7 W7,10,13, our IDNN chip achieves the reduced hardware footprint (0.53 mm2) and low power consumption (17.5 mW), manifesting the

advantage of the Fourier-based design as a scalable and power-efficient solution for data-heavy artificial intelligence applications. RESULTS DESIGN AND FABRICATION A typical electronic

one-layer neural network consists of an input layer, an output layer, connections between them (weight matrix), and elementwise nonlinearity (activation function). In a departure from the

electronic neural network, our introduced IDNN framework implements a convolution transformation physically in the optical field using PICs. The convolution transformation is special matrix

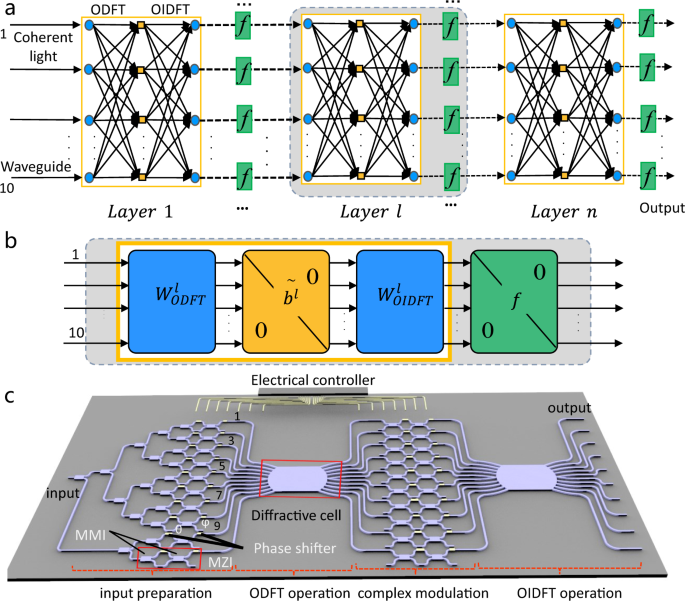
multiplication, and the complex-valued matrix elements are circulant41. The theoretical framework of the IDNN with multi-layers is shown in Fig. 1a. The preprocessed signals are encoded via

modulating the amplitude and phase (two degrees of freedom) of coherent light and then input to the multi-layer IDNNs. In each layer as depicted in Fig. 1b, the information propagates

through matrix multiplications followed by a nonlinear activation function. The linear part of each layer is composed of two ultracompact diffractive cells to implement optical discrete

Fourier transform (ODFT) operation (\({W}_{ODFT}^{l}\)) and optical inverse discrete Fourier transform (OIDFT) operation (\({W}_{OIDFT}^{l}\)), and a complex-valued transmission modulation

region in the Fourier domain behind the ODFT operation to achieve the Hadamard product. The nonlinear activation function _f_ originates from the intensity detection of the complex outputs.

We can hereby achieve a single-layer neural network. This IDNN can also be multi-layered by cascading multiple chips or recycling one single chip. The recycling process can be realized by

configuring the phase shifters through a computer-controlled digital-to-analog converter. Figure 1c shows the holistic diagram of the proposed silicon PICs-based IDNN chip, which consists of

four major sections, e.g., input preparation, ODFT operation, complex modulation, and OIDFT operation. A continuous-wave laser (wavelength 1550 nm) is incoupled into the device through a

grating coupler to realize the input source. The basic computing unit of a modulated MZI cell comprises multimode interferometers (MMI)-based beam splitters and two thermo-optic phase

shifters in the “input preparation” section. The internal phase shifters between two beam splitters (indicated as _θ_) and external beam splitters (indicated as _ϕ_) are used to control the

amplitude and phase of the input signals, respectively. All phase shifters are thermally tuned by the TiN heaters that are packaged to a printed circuit board (Fig. S5a). Then, they can be

manipulated by an external electric circuit controller. Subsequently, the ten input signals are fed into the diffractive cell, which is composed of a slab waveguide to implement the Fourier

transform in the “ODFT operation” section (details will be shown in Fig. 2). After the operation, an array of MZIs is utilized to modulate the amplitude and phase of the ten signals after

the ODFT operation. The modulated signals are then introduced to another diffractive cell to implement the OIDFT. After that, the ten output intensity signals are detected by an array of

photodetectors. In addition, a thermoelectric controller is implemented as the substrate beneath the chip to control and stabilize the temperature (details in Supplementary Note 2). The

holistic 3.2 mm × 2 mm chip monolithically integrates 10 modes, 20 MZIs, 2 slab waveguides, and 40 thermo-optic phase shifters. Figure 2a, b shows the optical micrographs of the whole chip

and the diffractive cell, respectively. The Fourier transform, as a core operation of our network, can be achieved using a slab waveguide-based ultracompact diffraction cell, whose input

waveguides are coded by different phase shifters incorporated in the “input preparation” section. The normalized electric field after the ODFT operation [_E_i (_k_)] (Supplementary Note 3)

can be expressed as $${E}_{i}(k)=\frac{1}{j\sqrt{{\lambda }_{0}R/{n}_{s}}}\int {E}_{0}(x)\exp (-j2\pi {f}_{k}x)dx$$ (1) where _E_0 is the input electric field, \({f}_{k}=k{n}_{s}/({\lambda

}_{0}R)\) is the angle spectrum of the incident light field, _λ_0 is the wavelength of light in vacuum, _R_ is the arc radius of the diffraction cell as shown in Fig. 2c, _n__s_ is the

effective refractive index of the waveguide, and _k_ is the axis of output coordinate plane. The simulated electric field distribution in the diffraction region and the output intensity

distribution is shown in Fig. 2c, d, respectively. The input light is centered into two central waveguides along the propagation direction and the outputs are the electric field profile

after the ODFT operation. The detailed analysis for light propagating in the entire chip is shown in Supplementary Note 3. The measured normalized intensities of ODFT operation in the

diffractive cell and the retrieved signal from all output channels after OIDFT operation are shown in Fig. 2e, f, respectively. The input signal can be well retrieved after ODFT and OIDFT

operations are applied with no intervening phase modulation as seen from Fig. 2f (more experimental results can be found in Fig. S7). IMAGE RECOGNITION WITH CORRELATION ALGORITHM To

demonstrate the performance of our IDNN chip and validate the design for realizing the convolution matrix, we first use the chip as a convolution operator to implement image recognition

using the correlation algorithm. The calibration for the initial amplitude and phase of the signal, the realization of ODFT and OIDFT operations, and the implementation of weight matrices

are shown in Supplementary Note 4. The detailed mathematical elucidation of correlation algorithms can be found in Supplementary Note 5. The 1D and 2D convolution operations have various

applications in machine learning, such as convolution layers in convolutional neural networks41,42,43 and correlation recognition of human faces from still images or video frames44,45. Here,

we demonstrate the cases of 1D sequence and 2D image recognitions using a classical correlation algorithm44, which demonstrates the capability of the convolution operation realized by our

IDNN chip. The image recognition process is shown in Fig. 3a. The correlation calculation of the input test image (_n_ × _n_) and target image (_m_ _×_ _m_) is conducted using the Hadamard

product between the Fourier transform of the input test image and the Fourier transform of a target image. Then the height of that peak (relative to the background) of the output result is

used to determine whether the test image matches the target image. The experimental recognized sequence ([10101]) is the same as the target sequence as shown in Fig. 3b (More results in Fig.

 S8). Furthermore, we extend the 1D sequence to 2D image recognition of digits (5 × 5 matrices) with the same correlation algorithm. The correlation signals for nine different digit-image

combinations are shown in Fig. 3c (details in Supplemental Note 6). Strong correlation peaks are observed along the diagonal line of the measured cross-correlation matrix, reflecting the

intuition that two images have maximum correlation and similarity when they are the same. Our approach to convolutional processing provides an effective method for accelerating computation

via reducing computational complexity, as compared with traditional methods43,41. The traditional electronic single convolution operation involves (_n_ − _m_ + _1_)2 matrix-vector

multiplication (MVM) operations with _n_ × _n_ and _m_ × _m_ dimension matrices43,41. Similarly, the state-of-the-art research works for photonic convolutional accelerators5,35 also perform

convolution operation by MVM operations, but in combination with parallel operations using WDM technology to accelerate the computing. Here, we realize an optical Fourier transform-based

convolution. Each 2D convolution with _n_ × _n_ and _m_ × _m_ dimension matrices needs (_n_ _−_ _m_ + _1_) × _m_ 1D convolution operations46. Since a 1D convolution is converted into an MVM

operation in our design, our approach only needs (_n_ _−_ _m_ + _1_) × _m_ MVM operations to compute a 2D convolution. This design can thus accelerate the convolution operations to achieve

improved scaling over traditional electronic counterparts43,41. More discussions on the computational convolution approach can be found in Supplementary Note 6. It can further be extended to

circulant convolution operation45 and employed in typical classification tasks47,48,49. IRIS FLOWER CLASSIFIER We demonstrate the performance of our network in classifying the Iris flower

dataset. Here we have four input parameters (the lengths and widths of the sepals and petals of a candidate flower). The task is to determine which of the three possible subspecies the

flower belongs to (_setosa, versicolor, and virginica_). We implement this classification task using a one-layer neural network with eight neurons as shown in Fig. 4a. The input and output

are connected by a complex, circulant weight matrix (_W_) with eight trained complex-valued parameters. Input signals are encoded by modulating the amplitude of the input field of the IDNN.

Amplitude and phase modulators in the Fourier domain are trained to map inputs into three output waveguides, which are detected by external power sensors. The highest intensity measurement

outcome is used to indicate the subspecies. The entire dataset with 150 instances is split into the training set and testing set according to a ratio of 8:2. The weights are trained only on

the training set. In the training process, the amplitude and phase of each channel in the Fourier domain are learnable parameters, representing a complex-valued modulation on the neural

network. Trained with the error back-propagation algorithm16, the numerical convergence of the accuracy and loss versus epoch number are depicted in Fig. S10. The training accuracy of 98.0%

is achieved in the complex modulation, while the training accuracy is 97.3% in the conventional one-layer fully connected neural network (Fig. S10). After training, the performance of the

IDNN chip with complex modulation is evaluated on the Iris flower classification testing dataset, see Fig. 4. The experimentally obtained energy distribution from the eight output waveguides

is shown in Fig. 4b for one testing data point as an example. The channel “0” has the highest output intensity, indicating that this flower is classified as “Setosa”. More experimental

results can be found in Fig. S10. The intensity distribution from the output detectors reveals that the IDNN can achieve a maximum signal at the corresponding detector channel identified

with candidate flower species. About 150 samples, including the training set and testing set, are extracted into two features and visualized as a scatter plot in Fig. 4c. A total of 30

testing samples are experimentally evaluated using the IDNN chip with only one wrong classification as marked by the red circle in Fig. 4c. The one-layer IDNN chip can achieve a high

classification accuracy of 96.7% over 30 testing images in the experiment (Fig. 4d), which is the same as the testing result (96.7%) of the conventional one-layer fully connected neural

network, manifesting that our IDNN has comparable accuracy with a fully connected network. However, our design has fewer components (i.e., the number of MZIs is reduced from 16 to 8) and

more efficient space overhead compared with the fully connected architectures. HANDWRITTEN DIGIT AND FASHION PRODUCT CLASSIFIER More complicated datasets, _MNIST_ (handwrite digits images),

and _Fashion-MNIST_ (clothing images) datasets are used to further validate the functionality of our IDNN chip. The two datasets are both split into the training (60,000 images) and testing

sets (10,000 images). Our model is trained on the entire training set, and 500 instances are uniformly and randomly drawn from the testing set to validate the trained model on-chip35. Figure

 5a shows that the network is composed of two layers, a hidden layer _W_ with 16 × 10 trained complex parameters and an output layer _W__out_ with ten trained complex parameters. The outputs

of the output layer are the recognition results (The computing details are shown in Supplementary Note 8). The numerical testing accuracy and loss vary with the epoch number as shown in

Fig. 5b with a classification accuracy of 92.5% (see Fig. S11). Besides, the simulated energy distribution from the intensity detection results of ten outputs is shown in Fig. S11f to

display the classification performance, indicating that our numerical simulations predict the channel with the highest energy will generally correspond to the correct handwritten digit. We

experimentally tested 500 images and the confusion matrix (Fig. 5c) shows an accuracy of 91.4% in the generated predictions, in contrast to 92.6% in the numerical simulation. The output

energy distributions from 10 waveguides for the classification of the digit “2” are depicted in Fig. 5d (More experimental results are shown in Fig. S12). These results show that we have

successfully implemented the classification task on the integrated diffractive optical computing platform. Our experimental testing accuracy is slightly lower (91.4%) than the numerically

predicted value obtained from simulations (92.6%), which is attributed to the errors from the diffractive region, heater calibration, and other experimental factors (Supplementary Note 10).

Although our method does not achieve as high accuracy as previous reservoir computing demonstrations50,51, their internal dynamics of reservoirs are uncontrollable with fixed nodes, which

leads to the stringent requirement of obtaining many parameters with high accuracy. Consequently, they are difficult to be implemented on chip. In contrast, our approach requires fewer

parameters in controllable weight matrices that significantly reduce the footprint and energy consumption. Meanwhile, the input data compression process in our method also loses some

information and lowers the numerical classification accuracy. The numerical blind testing accuracy (92.5%) with 10,000 samples can be further improved after enlarging the size of the network

with more input information. It is worth noting that the classification accuracy obtained with our approach is comparable to the fully connected network (Fig. 5b), but our method consumes

less energy and occupies less footprint, representing the major advantages of the design. We further use the IDNN to perform the classification of the _Fashion-MNIST_ dataset. In general, we

can encode the preprocessed signals by using the amplitude and phase channels of coherent light. In the case of the _MNIST_ dataset classifier, the output of the first hidden layer is

encoded to the amplitude channels of the output layer. To verify that the network also performs well when input signals are encoded into the phase channel, the signal from the input layer of

the fashion product images is encoded in the phase channel in our experiment. The numerical testing results for the classification of fashion products are depicted in Fig. S13. The

corresponding accuracy for 500 testing images with one hidden layer is 82.0% in simulation versus 80.2% in an experiment (Fig. 5f). The experimental energy distributions from ten waveguide

outputs using one image of a “pullover”, is shown in Fig. 5g and the experimental results from other images are depicted in Fig. S14. We implement additional experiments using the phase

channel encoding input signal on the _MNIST_ dataset and using the amplitude channel encoding input signal on the _Fashion-MNIST_ dataset. The confusion matrix for 500 images (Fig. S15a)

shows an experimental accuracy of 89.4%, in contrast to 92.6% for the numerical simulation results on the _MNIST_ dataset. The results for the _Fashion-MNIST_ dataset are 81.4% according to

the numerical simulations versus 80.4% for the experiment (Fig. S15b). We note that the accuracy error between the experimental and numerical results has no distinct difference between using

the amplitude channel and the phase channel. However, for phase encoding, the intensity of the input signal would not be attenuated, which leads to a higher output intensity in our

experiment. We compare our IDNN architecture with a fully connected neural network with the training results of the _MNIST_ dataset and _Fashion-MNIST_ dataset as shown in Fig. 5b, e,

respectively. The simulation model is built in Pytorch with a learning rate of 0.0001, a training period of 500 iterations, and a batch size of 100. Our complex circulant matrix-based neural

network with one hidden layer achieves a numerical testing accuracy of 92.5%, which is comparable to that obtained in both a fully connected neural network with one hidden layer (93.4%) and

a circulant matrix-based neural network with three-layers (93.5%) for the _MNIST_ dataset. For the _Fashion-MNIST_ dataset, both the simulated testing accuracies of the complex circulant

matrix-based neural network with one hidden layer and three layers are higher than 81% (81.7 and 83.2%, respectively), which is comparable with 83.0% for fully connected based algorithm. For

the _MNIST_ and _Fashion-MNIST_ datasets, the classification accuracy of our IDNN chip with less trainable parameters can be comparable with the traditional fully connected network. Our

IDNN chip can achieve comparable testing accuracy with classical fully connected neural networks in datasets _MNIST_ and _Fashion-MNIST_. Some key metrics evaluating the physical network are

listed by the comparison with the traditional fully connected MZI-based7,10,13 architectures for the optical realization, as shown in Table 1. For the _MNIST_ and _Fashion-MNIST_ datasets,

a 10 × 10 matrix on-chip is achieved with only 0.53 mm2 area and 17.5 mW power consumption to maintain the phase of heaters, while the traditional MZI-based ONN architectures need an area

around 5 mm2 and requisite energy consumption of 3–7 W. (More details are in Supplementary Notes 1). DISCUSSION We propose and experimentally demonstrate the reconfigurable IDNN chip,

leveraging diffractive optics to realize an efficient matrix-vector multiplication. Previous MZI-based integrated photonic approaches for computing have been predominantly restricted by

large footprints (around 0.5 mm2 per MZI unit23,26,29) and the excessive energy consumption to tune the phase, e.g., one needs ~50 mW to tune each thermo-optic heater (2π phase shift). Our

approach can effectively decrease footprints and energy consumption (see Table 1) by reducing the numbers of MZI from quadratic scaling with input data size to linear. The key strategy of

the scaling reduction is using integrated ultracompact diffractive cells (slab waveguides) to replace MZI units and realize Fourier transform operations. The slab waveguide is a passive

device with a small size (0.15 mm2) and does not require electric tuning. Our IDNN chip shows an equivalent classification capability while cutting down the number of optical basic

components (i.e., MZI modulators) to 10% of original on _MNIST_ and _Fashion-MNIST_ classification tasks and a half of original on the _Iris_ datasets, compared with the previous MZI-based

ONN architectures. We achieved a 10 × 10 matrix on-chip with 10 MZIs and two diffractive cells, which has an area of 0.53 mm2, while 100 MZIs are required with an area around 5 mm2 for a

fully connected network. Meanwhile, the power consumption used to maintain the phase of modulators, which is also the dominant source of energy consumption, decreases from 3–7 W (previous

techniques) to 17.5 mW (see Fig. S1). Using the compact design method, the matrix size can easily be scaled up to 64 × 64 with acceptable loss (see Supplementary Note 1). Considering the

current fabrication level of the integrated photonic chip, reduction in resource scaling from quadratic to linear and the relevant footprint and energy consumption reduction are profoundly

meaningful towards the goal of a large-scale programmable photonic neural network and the achievement of photonic AI computing. It is worth mentioning that the IDNN focuses on implementing

the convolution matrix with the advantages of scalability and low power consumption, instead of an arbitrary matrix-vector multiplication modulation. Since a convolution matrix contains

fewer free parameters than those in an arbitrary matrix, the current demonstrated one-layer network may not be an optimal solution for complicated classification tasks. This issue can be

mitigated by implementing multi-layers or multiple convolutions in each layer to obtain a stronger expression capability. The speed of IDNN is also limited by the electrical equipment and

can be accelerated when the modulators and detectors are high-speed programmed. Our integrated chip is adaptable to the Fourier-based convolution acceleration algorithm and multiple tasks,

which has great potentials for many applications in compact and scalable application-specific optical computing, future optical-artificial-intelligence computers, and quantum information

processing, such as image analysis, object classification, and live video processing in autonomous driving5,42. The footprint and energy consumption scale linearly with the input data

dimension, which will hugely reduce the resources used for future sophisticated and data-heavy computing, and facilitate the prospects of a power-efficient, ultracompact, and large-scale

integrated optical computing chip. METHODS FABRICATION The whole optical diffractive neural network is fabricated on the silicon-on-insulator (SOI) platform with a 220-nm thick silicon top

layer and a 2-μm thick buried oxide. Subsequently, a thin layer of titanium nitride (TiN) is deposited as the resistive layer for heaters. A thin aluminum film is patterned as the electrical

connection to the heaters and photodetectors. Isolation trenches are created by etching the SiO2 top cladding and Si substrate. ODFT OPERATION The critical part of the IDNN chip is the

ODFT/OIDFT operations composed of the diffractive regions with a suitable phase difference from different waveguides before the diffractive components. The phase shift, \({\phi }_{n-k}\),

between input _k_ and output _n_ can be designed to satisfy the relation \({{\phi }_{n-k}}=\frac{2 \pi }{N} (k-\frac{N-1}{2})(n-\frac{N-1}{2})\) by setting positions of input and output

waveguides. In addition, the phase offset \({\varphi }_{k}=\frac{\pi }{N} (N-1)k\) is additionally added to the input _k_ using length adjustment or a phase shift. Then the phase difference

\({\varDelta \phi }_{n}\) between two paths to the output _n_ originating from the inputs, _k_ + _1_ and _k_ is derived as \({{\Delta} {\phi}}_{n}=({\phi }_{n-(k+1)}+{\varphi }_{k+1})-({\phi

}_{n-k}+{\varphi }_{k})=\frac{2\pi n}{N}\). This allows the ODFT computation to be realized. CIRCULANT MATRIX For the linear part of the IDNN, a complex circulant matrix multiplication is

achieved utilizing ODFT and OIDFT operations. Assuming each circulant matrix _B_ is defined by a vector _b_, which is the first-row vector of _B_. Based on the theories of circulant

convolution52,53,54 and diffractive optics, the matrix-vector multiply can be efficiently performed using Fourier transform, which is expressed as

\({y}^{l+1}={W}_{OIDFT}^{l}[({W}_{ODFT}^{l}\,\circ {y}^{l})\circ \tilde{{b}^{l}}]={F}^{-1}[F(y^l)\circ F(b^l)]\). \({W}_{ODFT}^{l}\) is the matrix for ODFT, \({W}_{OIDFT}^{l}\) is the matrix

for OIDFT, _b__l_ is a vector of the circulant matrix _B_ of the _l_-layer neural network, _y__l_ is the input vector of the _l_-layer neural network. _F_(∘) represents an _n_-point ODFT

operation, \({{F}^{-1}} (\circ)\) is the inverse of _F_(∘) (OIDFT operation), ∘ represents the Hadamard product and \(\tilde{{b}^{l}}\) is the Fourier transform of _b__l_. NUMERICAL

SIMULATION The training process of Iris flower, Handwritten digit, and Fashion product datasets was conducted in Pytorch (Google Inc.), a package for Python. The training process of Iris

flower, Handwritten digit, and Fashion product datasets was conducted in Pytorch (Google Inc.), a package of Python. The learned complex parameter (_w_) is expressed as

\(w=a+{ib}=A{e}^{i\alpha }\) where _A_ is encoded into the internal phase shifters (_θ_) with \(\theta ={\mathrm arcsin }({A}^{2})\) and _α_ is encoded into the external phase shifters (_ϕ_)

with \(\phi =\alpha -\theta /2\). The ODFT and OIDFT operations are implemented using the angular spectrum method. A three-dimensional finite-difference-time-domain method is used to

simulate the optical field distribution and transmission spectra of the diffractive cells. DATA AVAILABILITY The data that support the findings of this study are available from the

corresponding authors on reasonable request. REFERENCES * Kitayama, K. et al. Novel frontier of photonics for data processing—Photonic accelerator. _APL Photonics_ 4, 090901 (2019). Article

  ADS  Google Scholar  * Caulfield, H. J., Kinser, J. & Rogers, S. K. Optical neural networks. _Proc. IEEE_ 77, 1573–1583 (1989). Article  Google Scholar  * O’Brien, J. L., Furusawa, A.

& Vuckovic, J. Photonic quantum technologies. _Nat. Photon_ 3, 687–695 (2009). Article  ADS  Google Scholar  * Kues, M. et al. On-chip generation of high-dimensional entangled quantum

states and their coherent control. _Nature_ 546, 622–626 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Feldmann, J. & Youngblood, N. et al. Parallel convolutional processing using

an integrated photonic tensor core. _Nature_ 589, 52–58 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Dong, P., Chen, Y. K., Duan, G. H. & Neilson, D. T. Silicon photonic devices

and integrated circuits. _Nanophotonics_ 3, 215–228 (2014). Article  CAS  Google Scholar  * Shen, Yichen et al. Deep learning with coherent nanophotonic circuits. _Nat. Photonics_ 11,

441–446 (2017). Article  ADS  CAS  Google Scholar  * Reck, M. et al. Experimental realization of any discrete unitary operator. _Phys. Rev. Lett._ 73, 58–61 (1994). Article  ADS  CAS  PubMed

  Google Scholar  * Harris, N. C. et al. Linear programmable nanophotonic processors. _Optica_ 5, 1623–1631 (2018). Article  ADS  CAS  Google Scholar  * Ribeiro, A. et al. Demonstration of a

4×4-port universal linear circuit. _Optica_ 3, 1348–1357 (2016). Article  ADS  CAS  Google Scholar  * Bogaerts, W. et al. Programmable photonic circuits. _Nature_ 586, 207–216 (2020).

Article  ADS  CAS  PubMed  Google Scholar  * Clements, W. R. et al. Optimal design for universal multiport interferometers. _Optica_ 3, 1460–1465 (2016). Article  ADS  Google Scholar  *

Zhang, H. et al. An optical neural chip for implementing complex-valued neural network. _Nat. Commun._ 12, 1–11 (2021). ADS  Google Scholar  * Tait, A. N. et al. Neuromorphic silicon

photonic networks. _Sci. Rep._ 7, 7430 (2016). Article  ADS  Google Scholar  * Feldmann, J. et al. All-optical spiking neurosynaptic networks with selflearning capabilities. _Nature_ 569,

208–214 (2019). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Wetzstein, G. et al. Inference in artificial intelligence with deep optics and photonics. _Nature_ 588, 39–47

(2020). Article  ADS  CAS  PubMed  Google Scholar  * Zhang, Y. et al. Temperature sensor with enhanced sensitivity based on silicon Mach-Zehnder interferometer with waveguide group index

engineering. _Opt. Express_ 26, 26057–26064 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Carolan, J. et al. Scalable feedback control of single photon sources for photonic quantum

technologies. _Optica_ 6, 335–340 (2019). Article  ADS  Google Scholar  * Estakhri, N. M., Edwards, B. & Engheta, N. Inverse-designed metastructures that solve equations. _Science_ 363,

1333–1338 (2019). Article  ADS  MathSciNet  MATH  Google Scholar  * Khoram, E. et al. Nanophotonic media for artificial neural inference. _Photonics Res._ 7, 823–827 (2019). Article  Google

Scholar  * Armitage, D. et al. High-speed spatial light modulator. _IEEE J. Quant. Electron_ 21, 1241–1248 (1985). Article  ADS  Google Scholar  * Li, S.-Q. et al. Phase-only transmissive

spatial light modulator based on tunable dielectric metasurface. _Science_ 364, 1087–1090 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Kagalwala, K. H., Di Giuseppe, G., Abouraddy,

A. F. & Saleh, B. E. A. Single-photon three-qubit quantum logic using spatial light modulators. _Nat. Commun._ 8, 739 (2017). Article  ADS  PubMed  PubMed Central  Google Scholar  * Zuo,

Y. et al. All-optical neural network with nonlinear activation functions. _Optica_ 6, 1132–1137 (2019). Article  ADS  CAS  Google Scholar  * Lu, T., Wu, S., Xu, X. & Francis, T.

Two-dimensional programmable optical neural network. _Appl. Opt._ 28, 4908–4913 (1989). Article  ADS  CAS  PubMed  Google Scholar  * Chang, J. L. et al. Hybrid optical-electronic

convolutional neural networks with optimized diffractive optics for image classification. _Sci. Rep._ 8, 12324 (2018). Article  ADS  PubMed  PubMed Central  Google Scholar  * Yuan, W. et al.

Fabrication of microlens array and its application: a review. _Chin. J. Mech. Eng._ 31, 1–9 (2018). Article  Google Scholar  * Luo, Y. et al. Design of task-specific optical systems using

broadband diffractive neural networks. _Light Sci. Appl._ 8, 112 (2019). Article  ADS  PubMed  PubMed Central  Google Scholar  * Psaltis, D., Brady, D., Gu, X. G. & Lin, S. Holography in

artificial neural networks. _Nature_ 343, 325–330 (1990). Article  ADS  CAS  PubMed  Google Scholar  * Yeh, S. L. et al. Optical implementation of the Hopfield neural network with matrix

gratings. _Appl. Opt._ 43, 858–865 (2004). Article  ADS  PubMed  Google Scholar  * Lin, X. et al. All-optical machine learning using diffractive deep neural networks. _Science_ 361,

1004–1008 (2018). Article  ADS  MathSciNet  CAS  PubMed  MATH  Google Scholar  * Mengu, D. et al. Analysis of diffractive optical neural networks and their integration with electronic neural

networks. _IEEE J. Sel. Top. Quant. Electron_ 26, 1–14 (2020). Article  Google Scholar  * Fan, F. et al. Holographic element-based effective perspective image segmentation and mosaicking

holographic stereogram printing. _Appl. Sci._ 9, 920 (2019). Article  Google Scholar  * Hamerly, R., Bernstein, L., Sludds, A., Soljačić, M. & Englund, D. Large-scale optical neural

networks based on photoelectric multiplication. _Phys. Rev. X_ 9, 021032 (2019). CAS  Google Scholar  * Xingyuan, X. et al. 11 TOPS photonic convolutional accelerator for optical neural

networks. _Nature_ 589, 44–51 (2021). Article  ADS  Google Scholar  * Silva, A. et al. Performing mathematical operations with metamaterials. _Science_ 343, 160–163 (2014). Article  ADS 

MathSciNet  CAS  PubMed  MATH  Google Scholar  * Colburn, S. et al. Optical frontend for a convolutional neural network. _Appl. Opt._ 58, 3179–3186 (2019). Article  ADS  PubMed  Google

Scholar  * Wang, J. et al. Multidimensional quantum entanglement with large-scale integrated optics. _Science_ 360, 285–291 (2018). Article  ADS  MathSciNet  CAS  PubMed  MATH  Google

Scholar  * Sun, J., Timurdogan, E., Yaacobi, A., Hosseini, E. S. & Watts, M. R. Large-scale nanophotonic phased array. _Nature_ 493, 195–199 (2013). Article  ADS  CAS  PubMed  Google

Scholar  * Harris, N. C. et al. Quantum transport simulations in a programmable nanophotonic processor. _Nat. Photon_ 11, 447–452 (2017). Article  ADS  CAS  Google Scholar  * Shafiee, A. et

al. ISAAC: a convolutional neural network accelerator with in-situ analog arithmetic in crossbars. _In Proc_. _2016 43rd Annual International Symposium on Computer Architecture_ (_ISCA_)

(IEEE, 2016). * He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In _2016 Proc_. _IEEE Conf. Computer Vision and Pattern Recognition_ (_CVPR_) (IEEE,

2016). * Gao, L., Chen, P. Y. & Yu, S. Demonstration of convolution kernel operation on resistive cross-point array. _IEEE Electron Device Lett._ 37, 870–873 (2016). Article  ADS  Google

Scholar  * Qiu, X., Zhang, D., Zhang, W. & Chen, L. Structured-pump-enabled quantum pattern recognition. _Phys. Rev. Lett._ 122, 123901 (2019). Article  ADS  CAS  PubMed  Google Scholar

  * Kumar, B. et al. Correlation pattern recognition for face recognition. _Proc. IEEE_ 94, 1963 (2006). Article  Google Scholar  * Gray, R. M. Toeplitz and circulant matrices: a review.

_now publishers inc._ 2, 155–239 (2006). * Suthaharan, S. _Machine Learning Models and Algorithms for Big Data Classification_ (Springer, 2016). * Nilsback, M-E. & Andrew Z. A visual

vocabulary for flower classification. In _2006_ _IEEE Computer Society Conference on Computer Vision and Pattern Recognition_ (CVPR'06) 2 (IEEE, 2006). * Krizhevsky, A., Ilya, S. &

Geoffrey, E. H. Imagenet classification with deep convolutional neural networks. _Adv. neural Inf. Process. Syst_. 25, 1097–1105 (2012). * Hermans, M., Soriano, M., Dambre, J., Bienstman, P.

& Fischer, I. Photonic delay systems as machine learning implementations. _J. Machine Learn Res_. 16, 2081–2097 (2015). * Antonik, P., Nicolas, M. & Damien, R. Large-scale

spatiotemporal photonic reservoir computer for image classification. _IEEE J. Sel. Top. Quant. Electron_ 26.1, 1–12 (2019). Google Scholar  * Ding, C.W., et al. Structured weight

matrices-based hardware accelerators in deep neural networks: Fpgas and asics. In _Proceedings of the 2018 on Great Lakes Symposium on VLSI_ (Association for Computing Machinery, 2018). *

Liang, Z., et al. Theoretical properties for neural networks with weight matrices of low displacement rank. In _Proc. 34th International Conference on Machine Learning_ 4082–4090 (JMLR.org,

2017). * Jiaqi, G. et al. Towards area-efficient optical neural networks: an FFT-based architecture. In _2020 25th Asia and South Pacific Design Automation Conference_ (_ASP-DAC_) (IEEE,

2020). Download references ACKNOWLEDGEMENTS This work was supported by the Singapore National Research Foundation under the Competitive Research Program (NRFCRP13-2014-01) and the Singapore

Ministry of Education (MOE) Tier 3 grant (MOE2017-T3-1-001). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Quantum Science and Engineering Centre (QSec), Nanyang Technological University,

Singapore, 639798, Singapore H. H. Zhu, J. Zou, H. Zhang, S. B. Luo, L. X. Wan, B. Wang, X. D. Jiang, L. C. Kwek & A. Q. Liu * National Key Laboratory of Science and Technology on

Micro/Nano Fabrication, Department of Micro/Nano Electronics, Shanghai Jiao Tong University, Shanghai, 200240, China Y. Z. Shi * Institute of Microelectronics, A*STAR (Agency for Science,

Technology and Research), Singapore, 138634, Singapore N. Wang & H. Cai * Centre for Quantum Technologies, National University of Singapore, Singapore, 117543, Singapore J. Thompson 

& L. C. Kwek * Advanced Micro Foundry, 11 Science Park Road, 117685, Singapore, Singapore X. S. Luo & L. Patrick * State Key Joint Laboratory of ESPC, Center for Sensor Technology of

Environment and Health, School of Environment, Tsinghua University, Beijing, 100084, China X. H. Zhou * Shanghai Engineering Research Center of Ultra-Precision Optical Manufacturing, School

of Information Science and Technology, Fudan University, Shanghai, 200433, China L. M. Xiao * Suzhou Institute of Nano-Tech and Nano-Bionics (SINANO), Chinese Academy of Sciences (CAS),

Suzhou, 215123, China W. Huang * Quantum Hub, School of Physical and Mathematical Science, Nanyang Technological University, 50 Nanyang Ave, 639798, Singapore, Singapore M. Gu Authors * H.

H. Zhu View author publications You can also search for this author inPubMed Google Scholar * J. Zou View author publications You can also search for this author inPubMed Google Scholar * H.

Zhang View author publications You can also search for this author inPubMed Google Scholar * Y. Z. Shi View author publications You can also search for this author inPubMed Google Scholar *

S. B. Luo View author publications You can also search for this author inPubMed Google Scholar * N. Wang View author publications You can also search for this author inPubMed Google Scholar

* H. Cai View author publications You can also search for this author inPubMed Google Scholar * L. X. Wan View author publications You can also search for this author inPubMed Google

Scholar * B. Wang View author publications You can also search for this author inPubMed Google Scholar * X. D. Jiang View author publications You can also search for this author inPubMed 

Google Scholar * J. Thompson View author publications You can also search for this author inPubMed Google Scholar * X. S. Luo View author publications You can also search for this author

inPubMed Google Scholar * X. H. Zhou View author publications You can also search for this author inPubMed Google Scholar * L. M. Xiao View author publications You can also search for this

author inPubMed Google Scholar * W. Huang View author publications You can also search for this author inPubMed Google Scholar * L. Patrick View author publications You can also search for

this author inPubMed Google Scholar * M. Gu View author publications You can also search for this author inPubMed Google Scholar * L. C. Kwek View author publications You can also search for

this author inPubMed Google Scholar * A. Q. Liu View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.H.Z., L.C.K., M.G., and A.Q.L. jointly

conceived the idea. H.H.Z., J.Z., H.Z., S.B.L., X.D.J., and A.Q.L. performed the numerical simulations and theoretical analysis. H.H.Z., J.Z., and L.X.W. did the experiments. H.H.Z., B.W.,

N.W., H.C., Y.Z.S., X.S.L., L.P., X.D.J., L.C.K., M.G., and A.Q.L. involved in the discussion and data analysis. H.H.Z., Y.Z.S., J.T., M.G., and A.Q.L. prepared the manuscript. X.H.Z.,

L.M.X., and W.H. revised the manuscript. L.C.K., M.G., and A.Q.L. supervised and coordinated all the work. All authors commented on the manuscript. CORRESPONDING AUTHORS Correspondence to X.

D. Jiang, X. H. Zhou, L. M. Xiao, M. Gu, L. C. Kwek or A. Q. Liu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION

_Nature Communications_ thanks Dong-Ling Deng, Miguel Soriano and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are

available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY

INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which

permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to

the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zhu, H.H., Zou, J., Zhang, H. _et al._ Space-efficient optical computing with an integrated chip diffractive neural network. _Nat Commun_

13, 1044 (2022). https://doi.org/10.1038/s41467-022-28702-0 Download citation * Received: 05 May 2021 * Accepted: 20 January 2022 * Published: 24 February 2022 * DOI:

https://doi.org/10.1038/s41467-022-28702-0 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative