News Reader.info

Download PDF Article Open access Published: 04 July 2024 Contextual quantum metrology Jeongwoo Jae  ORCID: orcid.org/0009-0004-2669-85201,2 na1, Jiwon Lee1 na1, M. S. Kim3, Kwang-Geol Lee 

ORCID: orcid.org/0000-0002-9795-44031 & …Jinhyoung Lee  ORCID: orcid.org/0000-0001-8920-44451,4 Show authors npj Quantum Information volume 10, Article number: 68 (2024) Cite this article

3322 Accesses

1 Altmetric

Metrics details

We demonstrate that the contextuality of measurement selection can enhance the precision of quantum metrology with a simple linear optical experiment. Contextuality is a nonclassical

property known as a resource for various quantum information processing tasks. Recent studies show that contextuality by anomalous weak values can be utilized to enhance metrological

precision, unraveling the role of contextuality in quantum metrology. Our contextual quantum metrology (coQM) scheme can elevate the precision of the optical polarimetry as much as 6 times

the precision limit given by the Quantum Fisher Information. We achieve the contextuality-enabled enhancement with two mutually complementary measurements, whereas, in the conventional

method, some optimal measurements to achieve the precision limit are either theoretically challenging to find or experimentally infeasible to realize. These results highlight that the

contextuality of measurement selection is applicable in practice for quantum metrology.

precision of macroscopic optical metrology Article Open access 11 January 2023 State-independent test of quantum contextuality with either single photons or coherent light Article Open

access 22 October 2021 Toward incompatible quantum limits on multiparameter estimation Article Open access 23 February 2023 Introduction

Precision measurement has played a crucial role in the development of natural science and engineering since measurement is a means for observing nature. As a technology for precision

measurement, quantum metrology has recently drawn attention with a wide range of applications such as microscopy1, imaging2,3, patterning4,5, gravitational wave detection6,7,8, and

timekeeping9,10. Quantum metrology enables measurements going beyond the precision of the standard quantum limit which can be obtained from the most-classical state in quantum physics. One

of the resources for precision enhancement is entanglement, a nonclassical property of quantum states11,12,13,14. However, an entangled state can easily lose its property through interaction

with other objects, while the interaction is inevitable in metrology. This makes it challenging to generate and manipulate an entangled state. Due to the limitations, it is difficult in

practice to attain the entanglement-enabled enhancement of precision. If easy-to-implement resources for metrology are found, the performance of quantum metrology can be greatly enhanced, as

well as its practicality. In this work, we demonstrate that the contextuality of measurement selection15, another nonclassical property, is an easy-to-implement resource for quantum

metrology.

Specifically, contextuality here refers to the dependency of quantum systems on measurement context16. Unlike classical predictions, quantum predictions for a given measurement can change

depending on whether another measurement is performed simultaneously or not. Bell–Kochen–Specker theorem first showed that quantum physics is contextual17,18, and this has been

experimentally proved on various quantum systems19,20,21,22. Also, it has been revealed that contextuality can be a resource for quantum information processing tasks such as quantum key

distribution23,24, universal quantum computing25, quantum state discrimination26, and quantum machine learning27,28. Recent studies show that contextuality caused by a post-selection and

weak measurement can be utilized to enhance metrological precision29,30,31. These works have fueled research directions to unravel the role of contextuality in quantum metrology.

To demonstrate the precision enhancement from the contextuality of measurement selection, we propose a method in quantum metrology which we call contextual quantum metrology (coQM). Unlike

conventional quantum metrology, the coQM utilizes two measurement settings and their contextuality. In our experiment, we adopt an optical polarimetry devised to measure the concentration of

sucrose solution32 and modify its scheme for the coQM. Our experiment employs two polarization measurements in mutually unbiased (or complementary) bases, and their selection context is

implemented by toggling a polarizing beam splitter ‘in’ and ‘out’ from its optical path. Our setup is scalable in that the size of the experiment does not increase along with the increase of

the number of probe photons. Also, the enhanced precision is attainable without error correction or mitigation which requires overhead33,34. We finally show that the precision of coQM can

go beyond the precision limit of conventional quantum metrology35,36,37 by a factor of 1.4–6.0.

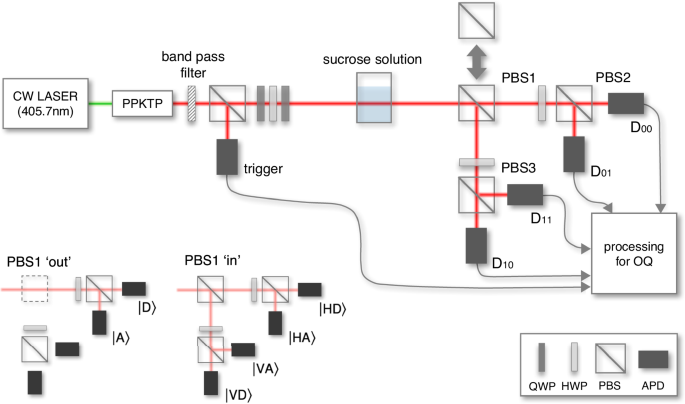
Figure 1 shows an experimental schematic for the coQM. Here, the coQM estimates the concentration of sucrose solution by following four steps: preparing a polarized single photon as a probe

light (see “Methods”), interacting the photon with the sucrose solution, measuring the polarization, and calculating an estimate via maximum likelihood estimator (MLE) using the operational

quasiprobability which will be discussed later as in Eq. (1). The photon interacts with the sucrose solution as it propagates through the solution. Afterwards, the photon polarization

rotates by angle αcl, where α, c, and l are the specific rotation of the sucrose solution, the concentration of the solution, and the traveling length of light in the solution,

respectively32. We can decide the concentration by measuring the polarization change for a given specific rotation and traveling length. All the procedures here look similar to those of the

conventional quantum metrology38, but the measurement and the estimation are steps that differentiate the coQM from the conventional approach.

Our probe state is a polarization state of a heralded single-photon source (see “Methods”). The probe polarization rotates by angle αlc when it propagates through the sucrose solution, where

α ≈ 34.1 deg ml dm−1 g−1 is the specific rotation of the sucrose solution, l = 0.1 dm is the traveling length of light in the solution, and c g ml−1 is the concentration of the solution. We

estimate the concentration c by measuring the polarization change. Here, we consider two measurement settings A and B, where A measures polarization in H/V basis and B does in a D/A basis

tilted 45° from the basis of A by half-wave plate (HWP). For triggered events, the probabilities of the polarization bases are determined from relative counts of four avalanche photodiodes

(APDs), D00, D01, D10, and D11. When polarizing beam splitter PBS1 is “out”, the measurement setup corresponds to the B measurement, and the counts on D00 and D01 determine probabilities of

\(\left\vert D\right\rangle\) and \(\left\vert A\right\rangle\), respectively. When the PBS1 is “in”, the measurement setup corresponds to the consecutive measurement performing A first and

B later, and the counts of D00, D01, D10, and D11 represent joint probabilities of \(\left\vert HD\right\rangle\), \(\left\vert HA\right\rangle\), \(\left\vert VD\right\rangle\), and

\(\left\vert VA\right\rangle\), respectively. We combine measuring data to construct operational quasiprobabiltiy (OQ) in Eq. (1), and an estimate is calculated with the maximum likelihood

estimator of OQ in Eq. (2). The coQM utilizes the context of selecting the measurement A to enhance its precision. Experimental results in Fig. 2 demonstrate the enhancement.

image

In the measurement step, the coQM employs two different polarization measurement settings A and B to utilize the contextuality of measurement selection therefrom15. A measures the

polarization in a specific basis \(\{\left\vert H\right\rangle ,\left\vert V\right\rangle \}\) and B does in a basis \(\{\left\vert D\right\rangle ,\left\vert A\right\rangle \}\) tilted 45°

from the basis of A by half-wave plate. (Note that the measurements are incompatible as their observable operators σz and σx do not commute, [σz, σx] ≠ 0.) Our basic setup is the measurement

by B, and we consider a context of whether measurement A is selected to be performed or not, prior to performing B. If A is not selected, the measurement B only is performed, and

probability is given by p(b∣B) for a binary value b. If A is selected, the experimental setup runs the consecutive measurement performing A first and B later. In this case, probability is

given by p(a, b∣A, B) for an outcome pair (a, b), where a is a binary outcome of A. Probabilities of B depend on whether an earlier A is performed for incompatible measurements A and B. The

probabilities of B when A is performed are unequal to those of B when A is not performed, i.e., p(b∣A, B) ≠ p(b∣B), where the marginal p(b∣A, B) = ∑ap(a, b∣A, B). We say they are

“contextual” in the context of measurement selection15. This is reflected in the operational quasiprobability w(a, b) in (1). We note that the term “contextual” or “contextuality” here is

not derived from Spekkens’ contextuality16 or quantum contextuality by the Kochen–Specker theorem18. (We will discuss that the contextuality of measurement selection stems from the

incompatibility of measurements39,40.) Our metrology utilizes the contextuality to enhance the precision of the polarimetry.

In the experiment (Fig. 1), the context of selecting A is established by toggling “in” the state of the polarizing beam splitter PBS1. Setting PBS1 “in”, the photon is consecutively measured

by two measurements A of H/V and B of D/A. Their outcome pairs (a, b) are identified by the clicks of the APDs Dab. When Dab clicks, the outcome of A is a, and the one of B is b. We note

that, as shown in Fig. 1, outcome a is determined by PBS1, while outcome b is by the subsequent PBS2 or PBS3; specifically, PBS2 and PBS3 are located 170 mm away from PBS1, much farther than

the coherence length of single-photon source Lc ≈ 0.052 mm (see “Methods”). In this regard, measurement A precedes B in time.

In the estimation step, we employ a statistical model, so-called operational quasiprobability41,42, which is given by

The context-free condition in our measurement setup is to assume that the prediction of measurement B is invariant under the context of selecting measurement A. This is called the condition

of no-signaling in time, represented by p(b∣B) = p(b∣A, B), ∀ b43. The crucial property of the operational quasiprobability is that, for the context-free condition, w is reduced to the

probability by the consecutive measurement, w(a, b) = p(a, b∣A, B), ∀ a, b. To the contrary, the quantum predictions violate the condition in general, w(a, b) ≠ p(a, b∣A, B), and w(a, b) can

even be negative-valued41,42.

The conventional quantum metrology estimates a physical parameter θ with an estimator based on a conditional probability p(x∣θ) for a data set \({\{{x}_{i}\}}_{i = 1}^{{N}_{{{{\rm{s}}}}}}\)

(see Supplementary Note 1). In the coQM, the operational quasiprobability plays a role in the conditional probability for the two data sets \({{{{\bf{x}}}}}_{B}={\{{b}_{i}\}}_{i =

1}^{{N}_{{{{\rm{s}}}}}}\) and \({{{{\bf{x}}}}}_{AB}={\{({a}_{j},{b}_{j})\}}_{j = 1}^{{N}_{{{{\rm{s}}}}}}\). In other words, the coQM calculates an estimate of polarization \(\check{\theta

}\) with a maximum likelihood estimator given by

where lW(θ∣xB, xAB) is a log-likelihood function for w (see “Methods”). The possible problem caused by this replacement is that w can be negative unlike the conditional probability, so that

the log-likelihood function diverges. However, we find that w remains positive for some range of parameters. We focus on the case for w to be applicable to the log-likelihood function

without the divergence problem. Finally, for an initial polarization θ0, we derive the estimate of concentration \(\check{c}\) from the polarization change as \(\check{c}=(\check{\theta

}-{\theta }_{0})/\alpha l\).

Our goal is to demonstrate the outperformance of the coQM over conventional quantum metrology. We employ the error of estimate Δθ, the standard deviation that the estimate differs from the

actual value, to quantify the performance of estimation. The smaller the error is, the more precise the estimate is.

As a baseline of performance, we take the conventional quantum metrology and its error given by quantum Fisher information (QFI) Fq, \(\Delta {\theta

}_{{{{\rm{q}}}}}=1/\sqrt{{N}_{{{{\rm{s}}}}}{F}_{{{{\rm{q}}}}}}\), where Ns is the number of samples. This is known as the lower bound of error in the conventional method. In the coQM, we

propose contextual Fisher information (coFI) to quantify the performance of the coQM,

\theta }\right)}^{2}.$$ (3)

In the asymptotic limit of Ns → ∞, the error of the coQM Δθco approaches to \(1/\sqrt{{N}_{{{{\rm{s}}}}}{F}_{{{{\rm{co}}}}}}\) (see Supplementary Note 2 for the asymptotic property and

estimator of coFI).

The coQM gains precision enhancement over the conventional quantum metrology if

Our method uses the two data sets xB and xAB. If each data set collects Ns samples, the total number of samples is 2Ns in our method. Reduction factor \(\sqrt{2}\) in the error by the

conventional is introduced, assuming the conventional take 2Ns samples (which is equivalent to comparing Fco to 2Fq).

We here suggest specific cases satisfying the criterion (4). Instead of a theoretical proof, we briefly summarize the theory behind the enhancement of precision by following arguments: For

the noncontextual model, the operational quasiprobability w(a, b∣θ) becomes the joint probability of the consecutive measurement p(a, b∣A, B). In this case, the coQM is reduced and

equivalent to the conventional quantum metrology using the consecutive measurement so that the Δθco equals or larger than Δθq (see Supplementary Note 1). For the contextual model,

conversely, Δθco can be smaller than Δθq (see ref. 40 for rigorous discussions). Figure 2a shows simulation results of the contextuality-enabled enhancement on the Bloch sphere.

Simulation and experiment results of the coQM.

a Landscape of error ratio of our Δθco to the conventional \(\Delta {\theta }_{{{{\rm{q}}}}}/\sqrt{2}\), \(R:= {\log }_{10}(\sqrt{2}\Delta {\theta }_{{{{\rm{co}}}}}/\Delta {\theta

}_{{{{\rm{q}}}}})\), on the Bloch sphere of a probe state \(\left\vert \psi \right\rangle =\cos (\theta /2)\left\vert H\right\rangle +{e}^{i\phi }\sin (\theta /2)\left\vert V\right\rangle\),

obtained by Monte-Carlo (MC) simulation. The coQM gains the contextuality-enabled enhancement if R < 0. The operational quasiprobability (OQ) is negative in the white regions. b Experiment

results of θ estimation. We prepare the probe states, \(\left\vert \psi \right\rangle{\rm{s}}\), by selecting 149 equiangular points from range 0.46π ≤ θ ≤ 0.55π for a fixed ϕ = 0.15π. For

each probe state \(\left\vert \psi \right\rangle\), we conduct θ estimation by drawing 105 samples (Ns = 105). Experiments (blue circles) assert that the coQM errors Δθco are smaller than

the minimum error in the conventional quantum metrology (cvQM) \(\Delta {\theta }_{{{{\rm{q}}}}}/\sqrt{2}=1/\sqrt{2{N}_{{{{\rm{s}}}}}{F}_{{{{\rm{q}}}}}}\) (dashed line), where quantum Fisher

information Fq = 1. The red solid line is the theoretical prediction, assuming the ideal optical setup. We characterize the actual experimental setup by applying a systematic error model

and use the resultant model parameters to make the theoretical prediction (blue solid line) (see Supplementary Note 3). c Sample-size dependency of estimation error Δθ. In the experiment, we

prepare a probe state with θ = 0.5π and ϕ = 0.1π. For small sample sizes, OQ can be negative by statistical fluctuation, which occasionally leads to estimation failures. For Ns = 102, the

failure rate is 88%, whereas the failure rate becomes significantly low for larger sample sizes and it is negligible for Ns ≥ 7 × 103. d We estimate concentrations c = 0.1, 0.3, and 0.5 g 

ml−1 with a probe state \(\left\vert \psi \right\rangle\) prepared with θ0 = 0.5π and ϕ = 0.15π. We draw Ns = 105 samples to estimate each concentration and repeat each estimation 10 times.

The error of concentration Δc comes from that of polarization Δθ by Δc = Δθ/αl. The error bar at each individual point represents Δcco. The green error bar in each concentration represents

the minimum error by the cvQM, \(\Delta {c}_{{{{\rm{q}}}}}/\sqrt{2}\).

We perform polarization estimation of θ with probe states prepared in \(\left\vert \psi \right\rangle =\cos (\theta /2)\left\vert H\right\rangle +{e}^{i\phi }\sin (\theta /2)\left\vert

V\right\rangle\) for 0.46π ≤ θ ≤ 0.55π and ϕ = 0.15π. For the probe states, the operational quasiprobability is given by \(w(a,b| \theta )=\left(1+{(-1)}^{a}\cos \theta +{(-1)}^{b}\sin

\theta \cos \phi \right)/4\). We draw Ns = 105 samples for each data set to construct the operational quasiprobability and calculate an estimate with the estimator (2). For polarization

estimation of θ, QFI Fq = 1, so the coQM gains the contextuality-enabled enhancement if \(\Delta {\theta }_{{{{\rm{co}}}}} < \Delta {\theta

}_{{{{\rm{q}}}}}/\sqrt{2}=1/\sqrt{2{N}_{{{{\rm{s}}}}}}\,\approx\, 2.24\times 1{0}^{-3}\). The errors of the coQM are smaller than the error limit of the conventional quantum metrology for

the whole selected range of θ (Fig. 2b). The worst case in our results has Δθco ≈ 1.53 × 10−3 around θ = π/2, and the best case has Δθco ≈ 3.7 × 10−4 around each end of the range of θ. This

demonstrates that our method elevates the precision of polarimetry by a factor of 1.4–6.0 from the limit of conventional quantum metrology.

We estimate sucrose solutions of three different concentrations c = 0.1, 0.3, and 0.5 g ml−1. We prepare the probe state with initial parameters θ0 = 0.5π and ϕ = 0.15π. For each

concentration, we repeat the estimation 10 times. The results (Fig. 2d) show that the errors of estimates by the coQM, Δcco, are smaller than the minimum error by the conventional quantum

metrology ( ≈ 5.9 × 10−2); For c = 0.1, 0.3 and 0.5 g ml−1, the mean errors are ≈ 3.7 × 10−2, ≈ 3.3 × 10−2, and ≈ 2.8 × 10−2, respectively. This illustrates that the coQM exceeds the

conventional quantum metrology by a wide margin.

These results illustrate the precision enhancement with the two incompatible measurements in the simple linear optical setup, whereas the conventional quantum estimation method requires

identifying an optimal measurement, which may often be experimentally challenging to implement in practice. We remark that the contextuality of measurement selection is an easy-to-implement

resource to enhance the precision of optical polarimetry.

The contextuality of measurement selection stems from the incompatibility of quantum measurements39. In the scenario of the consecutive measurement, if the two measurements A and B commute,

the consecutive measurement is de facto a single measurement; the probabilities p(b∣B) and p(b∣A, B) are equal, and the prediction for B is noncontextual. Otherwise, the prediction for

measurement B depends on whether performing the first measurement A is contextual except for a case when the initial state is prepared in an eigenstate of A. Thus, measurement

incompatibility is necessary for the contextuality of measurement selection. We experimentally verify that the measurements A and B are incompatible by testing complementarity44 (see

“Methods”).

The noncommutation of observable operators defines the incompatibility among measurements, represented by projection-valued measures (PVM), which we assume in the present work. The notion of

incompatibility needs to be generalized if the representation of measurement is generalized to positive operator-valued measure (POVM). This generalization is required, for example, if one

considers an open quantum system in a noisy environment. Non-joint measurability (non-JM) is one of the generalizations39. The non-JM plays an important role in a contextuality45,46, as does

the noncommutativity47. In fact, non-JM and the contextuality of measurement selection are also closely related as the negativity of operational quasiprobability is the necessary and

sufficient condition for non-JM40,48.

Recently, there were studies in a similar vein to the present work49,50, showing that noncommutativity can be a resource for quantum metrology. However, their schemes employ a post-selection

to discard unwanted measurement outcomes, so there is a tradeoff between success probability and Fisher information; success probability becomes small if Fisher information is large51.

Quantum post-selected metrology, such as weak value amplification methods, share this matter52,53. On the contrary, our method utilizes all of the measurement outcomes for the

estimation41,42, implying that the coQM is free from such tradeoff.

This work demonstrates that utilizing the contextuality of measurement selection can enhance the precision of measurement. The experiment attains precision beyond the limit of conventional

quantum metrology36,37. The coQM has advantages over the conventional method (see Supplementary Note 1): it can enhance the precision without optimizing the measurements if they are

incompatible, and it works even without any entangled state of a probe that has been regarded as difficult to generate and manipulate. We use the heralded single-photon source to clearly

show the performance of coQM per unit particle of probe. We expect that a multi-photon source can also be adopted for the coQM with similar settings of measurements15. Our method is expected

to be applicable to a quantum sensor54 if the context of measurement selection can be implemented within the sensor’s system. In addition, the approaches employed to demonstrate the

contextuality-enabled enhancements can be utilized to characterize quantum devices (see Supplementary Note 3), which is a fundamental task required to implement quantum

technologies.

We generate the heralded single photon as follows. High energy pump photons (p = 405.7 nm) from a continuous wave (CW) single mode laser (TOPMODE 405, TOPTICA) are sent to a periodically

poled KTP (PPKTP) crystal. PPKTP splits the input photons into photon pairs (signal and idler photons) through the type-II spontaneous parametric down-conversion (SPDC) process. The

polarizations of signal and idler photons are orthogonal to each other so that a polarizing beam splitter (PBS) can separate them into two different optical paths. The idler photon is sent

to an avalanche photodiode (APD) for triggering. The signal photon is sent to one of the four APDs (SPCM-QC4, Perkin Elmer). If the trigger APD is clicked, we count clicks on the four APDs.

We control the count rate of the trigger APD to be 2 × 105 cps to sufficiently suppress multi-photon events, i.e., \(\left\vert {{{\rm{SPDC}}}}\right\rangle \approx \left\vert

00\right\rangle +\epsilon \left\vert 11\right\rangle\) for ϵ ≪ 1. The click signals are post-processed by a field programmable gate array (FPGA) with a time bin size of 25 ns. The wavelength

λ and bandwidth Δλ of the single-photon source are 810 nm and 2 nm, respectively. The coherence length is given by Lc = λ2/2πΔλ ≈ 0.052 mm.

We prepare an initial probe state by using a series of three wave plates (Fig. 1), one half-wave plate (HWP), and two quarter-wave plates (QWP). After passing QWP1, HWP, and QWP2

sequentially, a horizontally polarized state \(\left\vert H\right\rangle\) becomes an initial state

}_{{{{\rm{in}}}}}\,=\,{{{{\rm{QWP}}}}}_{2}\left(\frac{\pi }{4}\right){{{\rm{HWP}}}}\left(p\right){{{{\rm{QWP}}}}}_{1}\left(q\right)\left\vert H\right\rangle \\

\qquad\quad\,=\,{e}^{i\left(-2p+q+\pi /4\right)}\left(\begin{array}{c}\cos \left(\frac{\pi }{4}-q\right)\\ {e}^{i\left(4p-2q-\frac{\pi }{2}\right)}\sin \left(\frac{\pi

}{4}-q\right)\end{array}\right),\end{array}$$ (5)

where p(q) is the angle of the fast axis of the half (quarter)-wave plate from the horizontal axis. The q value of QWP2 is fixed at π/4. By adjusting the control parameters p and q to

satisfy θ = π/2 − 2q and ϕ = 4p − 2q − π/2, we finally obtain the parameterized state \({\left\vert \psi \right\rangle }_{{{{\rm{in}}}}}=\cos (\theta /2)\left\vert H\right\rangle +{e}^{i\phi

}\sin (\theta /2)\left\vert V\right\rangle\).

The measurements \(A=\{{\hat{A}}_{a}\}\) and \(B=\{{\hat{B}}_{b}\}\) are incompatible as their observable operators σx and σz do not commute, i.e., [σx, σz] ≠ 0. These incompatible

measurements are also said mutually complementary44:

In our experiment, we test the complementarity through the probability of B after measuring A, p(b∣a) ≔ p(a, b∣A, B)/p(a∣A, B). For the data used in Fig. 2b, the average of probability

p(b∣a) is given by p(0∣0) = 0.4919, p(1∣0) = 0.5081, p(0∣1) = 0.4979, and p(1∣1) = 0.5021 with the error 2.4 × 10−3.

Maximum likelihood estimation is a method to find a parameter of a probability model which best describes observed data. This method assumes a likelihood function of the model, and maximizes

the function to determine the most likely value in the parameter space as an estimate. In this work, we take the operational quasiprobability as the model depending on the phase θ.

For the two data sets xB and xAB, we define the log-likelihood function as

\frac{1}{{N}_{{{{\rm{s}}}}}}\sum_{a,b=0}^{1}{N}_{W}(a,b)\log w(a,b| \theta ),$$ (7)

where \({N}_{W}(a,b)={N}_{AB}(a,b)+\left({N}_{B}(b)-{N}_{AB}(b)\right)/2\). NB(b) is the number of counts for outcome b in the data set xB, and NAB(a, b) is the number of counts for outcome

pair (a, b) in the data set xAB. NAB(b) is obtained by the marginal number of counts as NAB(b) = ∑aNAB(a, b). For a small number of samples, Nw(a, b) can be negative by statistical

fluctuations. We test whether the number count NW is positive, and neglect cases where the count is negative. For small sample sizes, the OQ count NW(a, b) can be negative by statistical

fluctuation, which occasionally leads to estimation failures. The experiment results in Fig. 2c show that the failure rate becomes significantly low for larger sample sizes, and it is

negligible for Ns ≥ 7 × 103.

In a broader sense, the coQM proposes an approach of integrating the two different ensembles for single-parameter estimation. To show that our estimator \(\check{\theta }\) is unbiased and

error of the estimate achieves Cramér–Rao bound55,56, we propose a theory that describes the operational quasiprobability as an ensemble mixture model (see Supplementary Note 2).

availability

The data generated from the optical experiment are available from the authors upon reasonable request.

The codes for the simulation of the optical experiment and the error analysis are available from the authors upon reasonable request.

References Casacio, C. A. et al. Quantum-enhanced nonlinear microscopy. Nature 594, 201–206 (2021).

Article  ADS  Google Scholar 

Treps, N. et al. Surpassing the standard quantum limit for optical imaging using nonclassical multimode light. Phys. Rev. Lett. 88, 203601 (2002).

Article  ADS  Google Scholar 

Brida, G., Genovese, M. & Ruo Berchera, I. Experimental realization of sub-shot-noise quantum imaging. Nat. Photonics 4, 227–230 (2010).

Article  ADS  Google Scholar 

Boto, A. N. et al. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 85, 2733–2736 (2000).

Article  ADS  Google Scholar 

Parniak, M. et al. Beating the Rayleigh limit using two-photon interference. Phys. Rev. Lett. 121, 250503 (2018).

Article  ADS  Google Scholar 

Abramovici, A. et al. Ligo: the laser interferometer gravitational-wave observatory. Science 256, 325–333 (1992).

Article  ADS  Google Scholar 

Collaboration, T. L. S. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7, 962–965 (2011).

Article  Google Scholar 

Aasi, J. et al. Enhanced sensitivity of the ligo gravitational wave detector by using squeezed states of light. Nat. Photonics 7, 613–619 (2013).

Article  ADS  Google Scholar 

Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced positioning and clock synchronization. Nature 412, 417–419 (2001).

Article  ADS  Google Scholar 

Pedrozo-Peñafiel, E. et al. Entanglement on an optical atomic-clock transition. Nature 588, 414–418 (2020).

Article  ADS  Google Scholar 

Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336 (2004).

Article  ADS  Google Scholar 

Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).

Article  ADS  MathSciNet  Google Scholar 

Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222 (2011).

Article  ADS  Google Scholar 

Tan, K. C. & Jeong, H. Nonclassical light and metrological power: an introductory review. AVS Quantum Sci. 1, 014701 (2019).

Article  ADS  Google Scholar 

Ryu, J. et al. Optical experiment to test negative probability in context of quantum-measurement selection. Sci. Rep. 9, 19021 (2019).

Article  ADS  Google Scholar 

Spekkens, R. W. Contextuality for preparations, transformations, and unsharp measurements. Phys. Rev. A 71, 052108 (2005).

Article  ADS  Google Scholar 

Bell, J. S. On the Einstein-Podolsky-Rosen paradox. Physics 1, 195–200 (1964).

Article  MathSciNet  Google Scholar 

Kochen, S. & Specker, E. P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 17, 59–87 (1967).

MathSciNet  Google Scholar 

Hasegawa, Y., Loidl, R., Badurek, G., Baron, M. & Rauch, H. Quantum contextuality in a single-neutron optical experiment. Phys. Rev. Lett. 97, 230401 (2006).

Article  ADS  Google Scholar 

Kirchmair, G. et al. State-independent experimental test of quantum contextuality. Nature 460, 494–497 (2009).

Article  ADS  Google Scholar 

Jerger, M. et al. Contextuality without nonlocality in a superconducting quantum system. Nat. Commun. 7, 12930 (2016).

Article  ADS  Google Scholar 

Zhang, A. et al. Experimental test of contextuality in quantum and classical systems. Phys. Rev. Lett. 122, 080401 (2019).

Article  ADS  Google Scholar 

Acín, A. et al. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).

Article  ADS  Google Scholar 

Reichardt, B. W., Unger, F. & Vazirani, U. Classical command of quantum systems. Nature 496, 456–460 (2013).

Article  ADS  Google Scholar 

Howard, M., Wallman, J., Veitch, V. & Emerson, J. Contextuality supplies the ‘magic’ for quantum computation. Nature 510, 351–355 (2014).

Article  ADS  Google Scholar 

Schmid, D. & Spekkens, R. W. Contextual advantage for state discrimination. Phys. Rev. X 8, 011015 (2018).

Google Scholar 

Gao, X., Anschuetz, E. R., Wang, S.-T., Cirac, J. I. & Lukin, M. D. Enhancing generative models via quantum correlations. Phys. Rev. X 12, 021037 (2022).

Google Scholar 

Anschuetz, E. R., Hu, H.-Y., Huang, J.-L. & Gao, X. Interpretable quantum advantage in neural sequence learning. PRX Quantum 4, 020338 (2023).

Article  ADS  Google Scholar 

Pusey, M. F. Anomalous weak values are proofs of contextuality. Phys. Rev. Lett. 113, 200401 (2014).

Article  ADS  Google Scholar 

Kunjwal, R., Lostaglio, M. & Pusey, M. F. Anomalous weak values and contextuality: robustness, tightness, and imaginary parts. Phys. Rev. A 100, 042116 (2019).

Article  ADS  Google Scholar 

Arvidsson-Shukur, D. R. M., McConnell, A. G. & Yunger Halpern, N. Nonclassical advantage in metrology established via quantum simulations of hypothetical closed timelike curves. Phys. Rev.

Lett. 131, 150202 (2023).

Article  ADS  MathSciNet  Google Scholar 

Yoon, S.-J., Lee, J.-S., Rockstuhl, C., Lee, C. & Lee, K.-G. Experimental quantum polarimetry using heralded single photons. Metrologia 57, 045008 (2020).

Article  ADS  Google Scholar 

Zhou, S., Zhang, M., Preskill, J. & Jiang, L. Achieving the Heisenberg limit in quantum metrology using quantum error correction. Nat. Commun. 9, 78 (2018).

Article  ADS  Google Scholar 

Maciejewski, F. B., Zimborás, Z. & Oszmaniec, M. Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography. Quantum 4, 257 (2020).

Article  Google Scholar 

Helstrom, C. W. Quantum detection and estimation theory. J. Stat. Phys. 1, 231–252 (1969).

Article  ADS  MathSciNet  Google Scholar 

Holevo, A. S. Probabilistic and Statistical Aspects of Quantum Theory (North-Holland, Amsterdam, 1982).

Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).

Article  ADS  MathSciNet  Google Scholar 

Liu, J., Yuan, H., Lu, X.-M. & Wang, X. Quantum fisher information matrix and multiparameter estimation. J. Phys. A 53, 023001 (2019).

Article  ADS  MathSciNet  Google Scholar 

Busch, P. Unsharp reality and joint measurements for spin observables. Phys. Rev. D 33, 2253–2261 (1986).

Article  ADS  MathSciNet  Google Scholar 

Jae, J., Lee, J., Lee, K.-G., Kim, M. S. & Lee, J. Metrological power of incompatible measurements. Preprint at arXiv https://doi.org/10.48550/arXiv.2311.11785 (2023).

Ryu, J., Lim, J., Hong, S. & Lee, J. Operational quasiprobabilities for qudits. Phys. Rev. A 88, 052123 (2013).

Article  ADS  Google Scholar 

Jae, J., Ryu, J. & Lee, J. Operational quasiprobabilities for continuous variables. Phys. Rev. A 96, 042121 (2017).

Article  ADS  Google Scholar 

Leggett, A. J. & Garg, A. Quantum mechanics versus macroscopic realism: is the flux there when nobody looks? Phys. Rev. Lett. 54, 857–860 (1985).

Article  ADS  MathSciNet  Google Scholar 

Lee, J., Kim, M. S. & Brukner, icv Operationally invariant measure of the distance between quantum states by complementary measurements. Phys. Rev. Lett. 91, 087902 (2003).

Article  ADS  Google Scholar 

Tavakoli, A. & Uola, R. Measurement incompatibility and steering are necessary and sufficient for operational contextuality. Phys. Rev. Res. 2, 013011 (2020).

Article  Google Scholar 

Gühne, O., Haapasalo, E., Kraft, T., Pellonpää, J.-P. & Uola, R. Colloquium: incompatible measurements in quantum information science. Rev. Mod. Phys. 95, 011003 (2023).

Article  ADS  Google Scholar 

Budroni, C., Cabello, A., Gühne, O., Kleinmann, M. & Larsson, J.-A. Kochen-specker contextuality. Rev. Mod. Phys. 94, 045007 (2022).

Article  ADS  Google Scholar 

Jae, J., Baek, K., Ryu, J. & Lee, J. Necessary and sufficient condition for joint measurability. Phys. Rev. A 100, 032113 (2019).

Article  ADS  MathSciNet  Google Scholar 

Arvidsson-Shukur, D. R. M. et al. Quantum advantage in postselected metrology. Nat. Commun. 11, 3775 (2020).

Article  ADS  Google Scholar 

Lupu-Gladstein, N. et al. Negative quasiprobabilities enhance phase estimation in quantum-optics experiment. Phys. Rev. Lett. 128, 220504 (2022).

Article  ADS  Google Scholar 

Combes, J., Ferrie, C., Jiang, Z. & Caves, C. M. Quantum limits on postselected, probabilistic quantum metrology. Phys. Rev. A 89, 052117 (2014).

Article  ADS  Google Scholar 

Ferrie, C. & Combes, J. Weak value amplification is suboptimal for estimation and detection. Phys. Rev. Lett. 112, 040406 (2014).

Article  ADS  Google Scholar 

Knee, G. C. & Gauger, E. M. When amplification with weak values fails to suppress technical noise. Phys. Rev. X 4, 011032 (2014).

Google Scholar 

Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).

Article  ADS  MathSciNet  Google Scholar 

Cramér, H. Mathematical Methods Of Statistics (Princeton University Press, 1946).

Rao, C. R. Information and the Accuracy Attainable in the Estimation of Statistical Parameters. In Breakthroughs in Statistics. (Springer Series in Statistics (Perspectives in Statistics).

Springer, New York, NY, 1992).

Download references

MSK acknowledges the EPSRC grants (EP/T00097X/1 and EP/Y0047542/1), KIST Open Research Programme, and AppQInfo MSCA ITN from the European Union Horizon 2020. KGL was supported by the

National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2023M3K5A109481312) and the Institute of Information and Communications Technology Planning &

Evaluation (IITP) grant funded by the Korean government (MSIT) (No. 2022-0-01026). J.L. was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government

(MSIT) (No. 2022M3E4A1077369), and Quantum Simulator Development Project for Materials Innovation(NRF-2023M3K5A1092818) through the National Research Foundation of Korea(NRF) funded by the

Korean government (Ministry of Science and ICT(MSIT)).

These authors contributed equally: Jeongwoo Jae, Jiwon Lee.

Authors and Affiliations Department of Physics, Hanyang University, Seoul, 04763, Republic of Korea

Jeongwoo Jae, Jiwon Lee, Kwang-Geol Lee & Jinhyoung Lee

R&D center, Samsung SDS, Seoul, 05510, Republic of Korea

Jeongwoo Jae

Blackett Laboratory, Imperial College London, London, SW7 2AZ, UK

M. S. Kim

Center for Quantum Simulation, Korea Institute of Science and Technology (KIST), Seoul, 02792, Republic of Korea

Jinhyoung Lee

AuthorsJeongwoo JaeView author publications You can also search for this author inPubMed Google Scholar

Jiwon LeeView author publications You can also search for this author inPubMed Google Scholar

M. S. KimView author publications You can also search for this author inPubMed Google Scholar

Kwang-Geol LeeView author publications You can also search for this author inPubMed Google Scholar

Jinhyoung LeeView author publications You can also search for this author inPubMed Google Scholar

Jeongwoo Jae, M. S. Kim, and Jinhyoung Lee contributed to the theoretical formulation of contextual quantum metrology. Jiwon Lee and Kwang-Geol Lee conducted the optical experiments and the

data analysis. All authors contributed to discussions in this work. Jeongwoo Jae wrote the paper with the assistance of other authors. Jeongwoo Jae and Jiwon Lee contributed equally to this

work.

Corresponding authors Correspondence to Kwang-Geol Lee or Jinhyoung Lee.

The authors declare no competing interests.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

informationRights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or

other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this articleCite this article Jae, J., Lee, J., Kim, M.S. et al. Contextual quantum metrology. npj Quantum Inf 10, 68 (2024). https://doi.org/10.1038/s41534-024-00862-5

Download citation

Received: 18 December 2023

Accepted: 21 June 2024

Published: 04 July 2024

DOI: https://doi.org/10.1038/s41534-024-00862-5

Share this article Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article.

Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative