News Reader.info

ABSTRACT Ferroelectricity in crystalline hafnium oxide has attracted considerable attention because of its potential application for memory devices. A recent breakthrough involves

electric-field-induced crystallization, allowing HfO2-based materials to avoid high-temperature crystallization, which is unexpected in the back-end-of-line process. However, due to the lack

of clarity in understanding the mechanisms during the crystallization process, we aim to employ theoretical methods for simulation, to guide experimental endeavors. In this work, we

extended our phase-field model by coupling the crystallization model and time-dependent Ginzburg-Landau equation to analyze the crystalline properties and the polarization evolution of

Hf0.5Zr0.5O2 thin film under applying an electric field periodic pulse. Through this approach, we found a wake-up effect during the process of crystallization and a transformation from

orthorhombic nano-domains to the stripe domain. Furthermore, we have proposed an innovative artificial neural synapse concept based on the continuous polarization variation under applied

electric field pulses. Our research lays the theoretical groundwork for the advancement of electric-field-induced crystallization in the hafnium oxide system. SIMILAR CONTENT BEING VIEWED BY

OTHERS ELECTRIC FIELD-INDUCED CRYSTALLIZATION OF FERROELECTRIC HAFNIUM ZIRCONIUM OXIDE Article Open access 15 November 2021 MECHANICAL-ELECTRICAL-CHEMICAL COUPLING STUDY ON THE

STABILIZATION OF A HAFNIA-BASED FERROELECTRIC PHASE Article Open access 09 December 2023 PIEZOELECTRICITY IN HAFNIA Article Open access 15 December 2021 INTRODUCTION With the discovery of

ferroelectricity in hafnium oxide first in 20111, it has gained significant attention owing to its application in many novel microelectronic memory devices like ferroelectric tunnel

junctions2,3, nonvolatile ferroelectric field effect transistors4, as well as ferroelectric capacitors5. Since its great Complementary Metal Oxide Semiconductor process compatibility,

thickness scalability, and other outstanding properties, HfO2-based ferroelectric devices have been shown as the primary material for a diverse range of cutting-edge and high-demand

applications. Under atmospheric temperature and pressure conditions, bulk HfO2 adopts a monoclinic structure with space group P21/c6. This structure is centrosymmetric, meaning it lacks the

necessary conditions for spontaneous polarization, which is essential for a genuine ferroelectric response. The discovery of ferroelectric properties in a fluorite-structured oxide initially

came as a surprise, and this ferroelectric response has been attributed to the presence of a non-centrosymmetric, metastable orthorhombic phase characterized by space group Pca211. In

previous research, various factors have been explored to enhance the stability of ferroelectric performance in hafnia. These include reducing the film thickness7, applying in-plane stress or

strain8, leveraging oxygen vacancies9, and doping with other elements10,11, which has been demonstrated to be one of the most important study subjects. As many HfO2-based devices can be

integrated into back-end-of-line (BEoL), recent research focused on hafnium zirconium oxide (HZO), for the feature facilitates low-temperature crystallization, aligning with the BEoL thermal

budget prerequisites12. However, the decrease of crystallization temperature is very important, especially for BEoL integration, recent research has discovered an innovative approach for

crystallization within the hafnium oxide system, specifically known as electric-field-induced crystallization. In this way, hafnium oxide is allowed to nucleate only at a very low

temperature, ~400 °C, and then crystalize under the application of an electric field13. Throughout the electric-field-induced transition process from the amorphous to the crystalline phase,

experimental observations have revealed that both crystallinity and polarization exhibit continuous variations with the application of a periodic electric-field pulse14. This phenomenon is

particularly noteworthy as it aligns with the desirable characteristics sought after in ferroelectric memory devices15,16 Theoretical study on HfO2-based ferroelectric material generally

revolves around the impact of elemental doping and different crystal grain orientations on ferroelectric performance17,18, Research involving electric-field-induced crystallization is still

limited as of now. Most of the works are modeling the process of field-induced crystallization for phase-change material19,20, However, the current phase-field models lack consideration for

the influence of crystallinity on polarization. This has resulted in significant challenges in research endeavors spanning both experiment and simulation. So, there is a pressing need to

expand the scope of simulation studies dedicated to electric-field-induced crystallization which can hold great promise in offering invaluable insights and guidance for experimental

endeavors in this domain. In this work, we extend our previous phase-field model21,22,23, into electric-field-induced crystallization to investigate the electric properties and domain

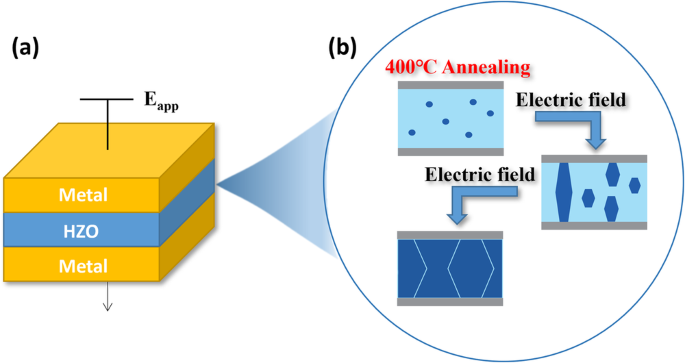
evolution during electric-induced HZO film crystallization. We assume that the crystallization of HZO film is under the application of an electric field pulse. As depicted in Fig. 1a, our

analysis focuses on HZO-based Metal-Ferroelectric-Metal stacks, which are commonly employed to characterize ferroelectric behavior. This approach directly paves the way for the integration

of ferroelectric memory devices. The HZO thin films are currently undergoing pre-nucleation annealing at lower temperatures, as illustrated in Fig. 1b, followed by growth under the influence

of an applied electric field. Our studies indicate that we can finely control the degree of crystallization and in consequence polarization in a highly precise manner. This capability

allows us to achieve common ferroelectric operations with a selected maximum remnant polarization. This work has practical significance, especially for ferroelectric artificial synapses,

where precise control of ferroelectric properties is crucial. RESULTS AND DISCUSSION CHARACTERIZATION OF ELECTRIC-FIELD-INDUCED CRYSTALLIZATION This work utilizes a 10 nm HZO film as the

model system for simulation to investigate the phenomena and properties during the process of electric-field-induced crystallization. The simulated results of crystallization are depicted in

Fig. 2. We initially simulate the pre-nucleation sites by generating random numbers, considering the spherical region with the nucleation size as radius as \(\eta \left(i,j,k\right)=1\),

corresponding to the ferroelectric phase. And the other region indicates the amorphous phase, where \(\eta \left(i,j,k\right)=0\). Then, an electric field pulse of 2 MV cm−1 is applied to

crystallization. Figure 2a displays the initial pre-nucleation stage and the process of crystallization under 1000, 2000, and 4000 electric field pulses, respectively. During the process of

crystallization, the P–E hysteresis of HZO film shows a wake-up effect as shown in Fig. 2b, which means that the hysteresis opens as the electric field is progressively cycled up and down.

Moreover, the remnant polarization values increasing from nearly zero to 24 µC cm−2 and the saturation polarization reaching 32 µC cm−2 will be found for a 10 nm thin film from simulation.

Additionally, in thermally-induced crystallization, the Johnson–Mehl–Avrami (JMA) equation can be applied to the crystallization process in a variety of amorphous solids24. So, we can also

utilize this method in our system aiming to validate the rationality of our crystallization model by fitting our results with the JMA equation. The JMA equation is the fractional amount of

crystallization as a function of time, which is given by $$\varphi (t)=1-\exp \left[-k{\left(\tau -t\right)}^{n}\right]$$ (1) where _φ_ is the degree of crystallinity, _t_ is time, _τ_ is

incubation time, _k_ is the reaction rate constant, and _n_ is Avrami exponent which is related to the behaviors of nucleation and growth25,26,27, As previously mentioned, there is a

pre-nucleation at a low temperature, so we consider the _τ_ = 0 in our model. Figure 2c shows the JMA equation fitting to our simulation data. The fitting result in a value of _n_ = 1.7,

which is considered close to 1.5, implies a diffusion-controlled spherical growth28. The crystallization behavior at varying electric field magnitudes is also simulated which is depicted in

Supplementary Fig. 1. As the electric field magnitude increases, the crystallization rate significantly accelerates. However, when the electric field is below the critical threshold,

electric-field-induced crystallization will not occur. To gain a profound understanding of electric-field-induced crystallization, we will analyze the evolution of domain structure during

this process. Figure 3 shows the simulated domain structure at different degrees of crystallinity of HZO film. The film size is 128 × 128 × 16 nm³, and the number of cells is 128 × 128 × 16.

Specifically, we established a grid comprising 17 layers, where the bottom 3 layers represent the substrate, the middle 10 layers describe the ferroelectric film and the top 3 layers for

the space above the film. The crystalline phase is consisted of four types of orthorhombic domains, labeled as \({O}_{1}^{+}\) phase, \({O}_{1}^{-}\) phase, \({O}_{2}^{+}\) phase and

\({O}_{2}^{-}\) phase. The blank areas indicate the absence of ferroelectric polarization, representing the amorphous phase. In the initial stage of crystallization, where the pre-nucleation

is considered to occupy 0.1 volume, most of the crystalline nuclei are single nano-domains because of their small size. Then, as the crystalline phase grows, nano-domains come into contact

with each other, forming stripe domains. During this process, most of these single domains are more inclined to form 60° and 120° domain walls. Eventually, all the amorphous phases transform

into ferroelectric phases, resulting in a checkerboard-like domain structure and the emergence of topological vortex domains composed of four different orthorhombic domains. The final

domain structure closely resembles the observed domain structure of HZO thin films in experiments1,18,29, referred to as the orthorhombic phase. To further verify the accuracy and

reliability of our model, we also conducted simulations of the crystallization process using the coefficient from another ref. 30 in which the content of hafnium oxide is 0.45 (see

Supplementary Figs. 3–5). The results exhibit similar crystallization behavior. The difference between the two simulated results is considered that mainly caused by the component of hafnium

oxide. And we also observed the wake-up effect in the P–E curves, and the domain structure is to be of the orthorhombic phase. THE ARTIFICIAL FERROELECTRICS SYNAPSE BASED ON CRYSTALLIZATION

Further, building upon a comprehensive understanding of the structural and electrical properties of HZO thin films, more synapse functions have been investigated. In artificial

ferroelectrics synapse, the operating principle demands that the relevant electrical performance responses will continuously change with consecutive input signals and can stabilize at a

long-lived state, which we consider as long-term potentiation (LTP) in neuromorphic engineering31. In the human brain, as a biological spike, the presynaptic membrane releases

neurotransmitters, leading to the generation of an action potential in the postsynaptic membrane. The artificial synapse shows similar behavior to biological synapses while most studies are

focused on ferroelectric tunnel junction devices, in which the reversal of polarization can induce a continuous variation of tunnel electroresistance32,33, Based on reference studies, a

structure with multiple HZO ferroelectric nano-islands on the substrate is fabricated. Each island can independently apply electric-field-induced crystallization, which is considered an

artificial spike, as shown in Fig. 4a. When applying an external electric field, the amorphous HZO begins to crystallize. And we can store different information by controlling crystallinity

in each island. As the gradual crystallization of HZO film under the influence of an external electric field, the polarization performs a continuous increase with applying electric field

cycling at 2 MV cm−1, which is shown in Fig. 4b. The trend of increasing polarization is similar to the trend of increasing crystallinity, further indicating that polarization magnitude is

correlated with crystallinity. We have selected four points on the graph, denoted as state 0, state 1, state 2, and state 3, which represent four distinct states for information storage,

aiming to simulate the performance of artificial neural synapses. Here we consider a training pulse as 2 MV cm−1 and a readout pulse as 1 MV cm−1. Taking state 1 as an example, we examine

the changes in polarization response under 100 cycles of applying training and readout pulses. As is demonstrated in Fig. 4c, the result shows that the training pulse will cause an increase

of polarization, while the readout pulse stabilizes the polarization. The stability of other states is also simulated, which is shown in Fig. S2. In this manner, we have proposed a training

approach within ferroelectric HZO thin films to simulate neural synapses leveraging its property of continuous variation of crystallinity and polarization of HZO under prolonged excitation

by an external electric field. The entire training process is illustrated in Fig. 4d as shown below. In summary, we have successfully extended the phase-field model based on the

time-dependent Ginzburg-Landau (TDGL) equation by coupling the crystallization model, which can analyze the evolution of dynamic polarization during the process of electric-field-induced

crystallization. An order parameter \(\eta \left(i,j,k\right)\) is introduced in our phase-field model, which is used to describe the transformation from an amorphous phase to a crystalline

phase. We validate the electric-field-induced crystallization process by analyzing the variation of \(\eta \left(i,j,k\right)\) and observing the wake-up effect of polarization hysteresis by

applying a 2 MV cm−1 electric field pulse for more than 4000 cycles. This result is close to the JMA equation as well. It was found that the remanent polarization can increase to 24 µC cm−2

and maximum polarization reach 32 µC cm−2 during the wake-up process. The evolution of polarization from a single nano-domain to a stripe domain is also demonstrated in our simulation. The

crystalline phase mainly consists of four types of orthorhombic phase which aligns with the observation of HZO film in experiments. Finally, we proposed an artificial neural synapse device

leveraging the property that allows for continuous polarization variation under electric field pulses. Through our simulation, we have verified the LTP properties under training signals and

the stability under multiple readout signals. This demonstrates that electric-field-induced crystalline HZO holds promise as a candidate for electric artificial synapses. METHODS PHASE-FIELD

MODELING OF ELECTRIC-FIELD-INDUCED CRYSTALLIZATION Our method couples the crystallization model and the TDGL equation. In the crystallization model, we introduce an order parameter denoted

as \(\eta (i,j,k)\) to differentiate between the crystal phase and the amorphous phase. The evolution equation for the order parameter is \(\eta \left(i,j,k\right)\) given as follows:

$$\frac{\partial \eta \left(i,j,k\right)}{\partial t}=-L\frac{\delta F}{\delta \eta (i,j,k)}$$ (2) where _L_ is the kinetic coefficient. And _F_ is the total energy of two systems, which can

be written as, $$F={\int }_{\!V}\left[{\varepsilon }^{2}{\nabla }_{\eta(i,j,k)}^{2}+f\left[\right.\eta (i,j,k)\right]dV$$ (3) where _ε_ is the gradient energy coefficient, and ∇η is the

gradient distribution of _η_(i, j, k). As the hafnium oxide system has many complex crystalline phases, for simplicity, we assume that all the grains in the simulated microstructure are

ferroelectric. As a result, we only need to consider the transformation process from the amorphous phase to the ferroelectric phase. In this way, the _η(i, j, k)_ can be described by a

double-well function: $$f\left[{\rm{\eta }}\left({\rm{i}},{\rm{j}},{\rm{k}}\right)\right]={\rm{H}}{{\rm{\eta }}}^{2}\left({\rm{i}},{\rm{j}},{\rm{k}}\right)\left[1-{\rm{\eta

}}\left({\rm{i}},{\rm{j}},{\rm{k}}\right)\right][1-{\rm{\eta }}\left({\rm{i}},{\rm{j}},{\rm{k}}\right)+\Delta{\rm{\mu }}]\left\}\right.$$ (4) where _H_ is potential well depth, ∆_μ_ is

related to the driving force in the electric-field-induced crystallization system. If _η(i, j, k)_ equals 0, it means that the unit is amorphous. While _η(i, j, k)_ equals 1, it corresponds

to the crystalline (ferroelectric) phase. Since electric-field-induced crystallization is a complicated transformation process, we assumed that the driving force in this system could be

analogously compared to thermally-induced crystallization. In the process of thermally induced crystallization, increasing the temperature enhances the thermal motion of atoms or molecules,

leading them to rearrange and form a crystalline structure34. Similarly, in the context of electric-field-induced crystallization, the application of an electric field can alter the

arrangement of atoms or molecules within the material, facilitating the transition to a crystalline state. So, the driving force ∆_μ_ in Eq. (3) can be considered depending on the applied

electric field and the stability of crystallization, which can be given as $$\Delta \mu ={\rm{\beta }}\left({\varphi }_{{\rm{stable}}}-\varphi \right)\left\{\exp

[E(i,j,k)-{{\rm{E}}}_{{\rm{crit}}}]-1\right\}$$ (5) where _β_ is a defined coefficient related to the driving force, \({\rm{\varphi }}=\frac{\sum {\rm{\eta

}}\left({\rm{i}},{\rm{j}},{\rm{k}}\right)}{{nx}\times {ny}\times {nz}}\) which represent the current degree of crystallinity. And \({{\rm{\varphi }}}_{{\rm{stable}}}\) is the stable degree

of crystallinity, _E(i, j, k)_ is the local electric field, and _E_cri is the critical electric field to crystallization. For phase transition analysis in ferroelectric materials, we

typically choose polarization _P__i_(_r,t_) as the order parameter. Based on the principle of energy minimization, the temporal evolution of spatially inhomogeneous polarization behavior in

the ferroelectric layer can be described by the TDGL equation35,36: $$\frac{\partial {P}_{i}\left(r,t\right)}{\partial t}=-L\frac{\delta F}{\delta

{P}_{i}\left(r,t\right)},\left(i=1,2,3\right)$$ (6) where _L_ is the kinetic coefficient components relating to the domain switching, _t_ is the time, and _F_ is the total free energy of the

system, which can be given as: $$F=\int \left({f}_{{\rm{bulk}}}+{f}_{{\rm{grad}}}+{f}_{{\rm{ela}}}+{f}_{{\rm{dep}}}+{f}_{{\rm{appl}}}\right){dV}$$ (7) where _f_bulk, _f_grad, _f_ela, and

_f_appl are the contributions from bulk free energy, gradient energy, elastic strain energy, depolarization energy, and applied electric field, respectively. The bulk free energy can be

expressed as a function of various parameters such as temperature, pressure, and composition. It plays a crucial role in determining the equilibrium state of a system and can be used to

predict phase changes, chemical reactions, and other thermodynamic behaviors. So, the order parameters _P_(_r,t_) and _η_(_i, j, k_) are coupled by bulk free energy:

$$\begin{array}{ll}{f}_{{\rm{bulk}}}=\eta (i,j,k)\left[{a}_{1-{\rm{FE}}}({P}_{1}^{2}+{P}_{2}^{2}+{P}_{3}^{2})\right]+\left[1-\eta

(i,j,k)\right]\left[{a}_{1-{\rm{amor}}}({P}_{1}^{2}+{P}_{2}^{2}+{P}_{3}^{2})\right]\\\qquad\quad +\,\eta

(i,j,k)\left[{a}_{11-{\rm{FE}}}({P}_{1}^{4}+{P}_{2}^{4}+{P}_{3}^{4})\right]+\left[1-\eta (i,j,k)\right]\left[{a}_{11-{\rm{amor}}}({P}_{1}^{4}+{P}_{2}^{4}+{P}_{3}^{4})\right]\\\qquad\quad

+\,\eta (i,j,k)\left[{a}_{111-{\rm{FE}}}({P}_{1}^{6}+{P}_{2}^{6}+{P}_{3}^{6})\right]+\left[1-\eta

(i,j,k)\right]\left[{a}_{111-{\rm{amor}}}({P}_{1}^{6}+{P}_{2}^{6}+{P}_{3}^{6})\right]\end{array}$$ (8) where \({a}_{1-{\rm{FE}}}\), \({a}_{11-{\rm{FE}}}\), \({a}_{111-{\rm{FE}}}\),

\({a}_{1-{\rm{amor}}}\), \({a}_{11-{\rm{amor}}}\), \({a}_{111-{\rm{amor}}}\) are the Landau coefficient of the ferroelectric phase and amorphous phase respectively. It should be noted that

the Landau energy does not include the coupling coefficient of the ferroelectric phase and amorphous phase, like \({a}_{12-{\rm{FE}}},{a}_{12-{\rm{amor}}}\). This is because not considering

it will not affect the main result29. The Landau coefficients are listed as follows18,37, \({a}_{1-{\rm{FE}}}=-1.1\times {10}^{9}{C}^{-2}{m}^{2}N,{a}_{11-{\rm{FE}}}=-1.98\times

{10}^{10}{C}^{-4}{m}^{6}N,{a}_{111-{\rm{FE}}}=-1.6\times {10}^{11}{C}^{-6}{m}^{10}N,{a}_{1-{\rm{amor}}}=1.6\times {10}^{8}{C}^{-2}{m}^{2}N,{a}_{11-{\rm{amor}}}=1.8\times

{10}^{13}{C}^{-4}{m}^{6}N,{a}_{111-{\rm{amor}}}=0\). The gradient energy in the ferroelectric system is also regarded as the domain-wall energy, which originates from the inhomogeneous

distribution of polarization in the film. The expression of gradient energy is as follows $${f}_{{\rm{grad}}}=\frac{1}{2}{G}_{{ijkl}}{P}_{i,j}{P}_{k,l}$$ (9) where \({P}_{i,j}=\partial

{P}_{i}/\partial {x}_{j}\), and _G__ijkl_ is the gradient energy coefficient. The elastic strain energy is based on elasticity theory, which can be described as

$${f}_{{\rm{elas}}}=\frac{1}{2}{C}_{{ijkl}}\left({\varepsilon }_{{ij}}-{\varepsilon }_{{ij}}^{0}\right)\left({\varepsilon }_{{kl}}-{\varepsilon }_{{kl}}^{0}\right)$$ (10) where _C__ijkl_ is

the elastic stiffness tensor, _ε__ij_ is the total strain of the system, and \({\varepsilon }_{{ij}}^{0}\) is intrinsic strain, which means the strain produced by the materials without

external stress. The electrostatic free energy density consists of the depolarization field and the external electric field, which are given by $${f}_{{\rm{dep}}}=-\frac{1}{2}{{\varepsilon

}_{0}{\varepsilon }_{{\rm{r}}}E}_{i}{E}_{j}$$ (11) $${f}_{{\rm{appl}}}=-{E}_{i}{P}_{i}$$ (12) where _ε_0 is vacuum permittivity, _ε__r_ is the dielectric constant, and _E__i_ is the local

electric field. DATA AVAILABILITY The data that support the findings of this study are available from the corresponding author upon reasonable request. CODE AVAILABILITY The codes that

support the findings of this study are available from the corresponding author upon reasonable request. REFERENCES * Böscke, T. S., Müller, J., Bräuhaus, D., Schröder, U. & Böttger, U.

Ferroelectricity in hafnium oxide thin films. _Appl. Phys. Lett._ 99, 102903 (2021). Article  ADS  Google Scholar  * Toriumi, A. et al. Material perspectives of HfO2-based ferroelectric

films for device applications. IEDM Technical Digest. 15.1.1–15.1.4 (2019). * Wang, J. et al. Microscopic physical origin of polarization induced large tunneling electroresistance in

tetragonal-phase BiFeO3. _Acta Mater._ 225, 117564 (2022). Article  Google Scholar  * Müller, J. et al. Ferroelectricity in HfO2 enables nonvolatile data storage in 28 nm HKMG. In _Proc IEEE

Symposium on VLSI Technology_. 25–26 (2012). * Hoffmann, M. et al. Direct observation of negative capacitance in polycrystalline ferroelectric HfO2. _Adv. Funct. Mater._ 26, 8643–8649

(2016). Article  Google Scholar  * Sang, X. H., Grimley, E. D., Schenk, T., Schroeder, U. & LeBeau, J. M. On the structural origins of ferroelectricity in HfO2 thin films. _Appl. Phys.

Lett._ 106, 162905 (2015). Article  ADS  Google Scholar  * Cheema, S. S. et al. Enhanced ferroelectricity in ultrathin films grown directly on silicon. _Nature_ 580, 478–482 (2020). Article

  ADS  Google Scholar  * Ihlefeld, J. F. et al. Applied in-plane strain effects on the polarization response of ferroelectric hafnium zirconium oxide thin films. _Appl. Phys. Lett._ 123,

082901 (2023). Article  ADS  Google Scholar  * Zhou, Y. et al. The effects of oxygen vacancies on ferroelectric phase transition of HfO2-based thin film from first-principle. _Comp. Mater.

Sci._ 167, 143–150 (2019). Article  ADS  Google Scholar  * Martin, D. et al. Ferroelectricity in Si-doped HfO2 revealed: a binary lead-free ferroelectric. _Adv. Mater._ 26, 8198–8202 (2014).

Article  Google Scholar  * Lu, J. Y. W., Shieh, J. & Tsai, F. Y. Induction of ferroelectricity in nanoscale ZrO2/HfO2 bilayer thin films on Pt/Ti/SiO2/Si substrates. _Acta Mater._ 115,

68–75 (2015). Article  ADS  Google Scholar  * Lehninger, D. et al. Back-end-of-line compatible low-temperature furnace anneal for ferroelectric hafnium zirconium oxide formation. _Phys.

Status Solidi A_ 217, 1900840 (2020). Article  ADS  Google Scholar  * Lederer, M. et al. On the origin of wake-up and antiferroelectric-like behavior in ferroelectric hafnium oxide. _Phys.

Status Solidi_ 15, 2100086 (2021). Google Scholar  * Lederer, M. et al. Electric-field-induced crystallization of ferroelectric hafnium zirconium oxide. _Sci. Rep._ 11, 22266 (2021). Article

  ADS  Google Scholar  * Wang, J. et al. Ferroelectric domain-wall logic units. _Nat. Commun._ 13, 3255 (2022). Article  ADS  Google Scholar  * Shi, X. et al. Ultrafast ferroelectric domain

switching induced by nano‐second strain‐pulse. _Adv. Theory Simul._ 5, 1–7 (2022). Article  Google Scholar  * Saha, A. K., Grisafe, B., Datta, S.& Gupta, S. K. Microscopic crystal phase

inspired modeling of Zr concentration effects in Hf1-_x_Zr_x_O2 thin films. In _Proc._ _IEEE Symposium on VLSI Technology._ 226–227 (2019). * Sugathan, S., Thekkepat, K., Bandyopadhyay, S.,

Kim, J. & Cha, P. R. A phase field model combined with a genetic algorithm for polycrystalline hafnium zirconium oxide ferroelectrics. _Nanoscale_ 14, 14997–15009 (2022). Article  Google

Scholar  * Levi, A. C. & Kotrla, M. Theory and simulation of crystal growth. _J. Phys. Condens. Matter_ 9, 299–344 (1997). Article  ADS  Google Scholar  * Gilmer, G. H. & Bakker, A.

F. Molecular dynamics simulations of steps at crystal surfaces. _MRS Proc._ 209, 135–145 (1990). Article  Google Scholar  * Guo, C. et al. Strain-induced toroidal polar states in wrinkled

ferroelectric polymer by phase-field simulations. _Adv. Electron. Mater._ 9, 2300193 (2023). Article  Google Scholar  * Shao, C., Shi, X., Wang, J., Xu, J. & Huang, H. Designing

ultrafast cooling rate for room temperature electrocaloric effects by phase-field simulations. _Adv. Theory Simul._ 5, 2200406 (2022). Article  Google Scholar  * Liu, D. et al. Phase-field

simulations of vortex chirality manipulation in ferroelectric thin films. _npj Quantum Mater._ 7, 34 (2022). Article  ADS  Google Scholar  * Mandal, S., Lee, D. E. & Park, T. Isothermal

crystallization kinetics of (Cu60Zr25Ti15)99.3Nb0.7 bulk metallic glass. _Sci. Rep._ 10, 10577 (2020). Article  ADS  Google Scholar  * Johnson, W. A. & Mehl, R. F. Reaction kinetics in

processes of nucleation and growth. _Trans. Am. Inst. Met. Pet. Eng._ 135, 416–458 (1939). Google Scholar  * Avrami, M. Kinetics of phase change. II Transformation‐time relations for random

distribution of nuclei. _J. Chem. Phys._ 8, 212–224 (1940). Article  ADS  Google Scholar  * Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. III. _J. Chem.

Phys._ 9, 177–184 (1940). Article  ADS  Google Scholar  * Shirzad, K. & Viney, C. A critical review on applications of the Avrami equation beyond materials science. _J. R. Soc.

Interface_ 20, 20230242–20230242 (2023). Article  Google Scholar  * Lai, B. et al. Study on the phase transition dynamics of HfO2-based ferroelectric films under ultrafast electric pulse.

_J. Phys. Condens Matter_ 33, 405402 (2021). Article  Google Scholar  * Anna, N. et al. Eliseev. Effective Landau-type model of a HfxZr1−xO2-graphene nanostructure. _Phys. Rev. Appl._ 20,

054007 (2023). Article  Google Scholar  * Ohno, T. et al. Short-term plasticity and long-term potentiation mimicked in single inorganic synapses. _Nat. Mater._ 10, 591–595 (2011). Article 

ADS  Google Scholar  * Chanthbouala, A. et al. A ferroelectric memristor. _Nat. Mater._ 11, 860–864 (2021). Article  ADS  Google Scholar  * Garcia, V. et al. Giant tunnel electroresistance

for non-destructive readout of ferroelectric states. _Nature_ 460, 81–84 (2009). Article  ADS  Google Scholar  * Milica, M. et al. Thermally-induced crystallization of amorphous

Fe40Ni40P14B6 alloy. _Thermochim. Acta_ 614, 129–136 (2015). Article  Google Scholar  * Li, Y. L., Hu, S. Y., Liu, Z. K. & chen, L. Q. Phase-field model of domain structures in

ferroelectric thin films. _Appl. Phy. Lett._ 78, 3878–3880 (2001). Article  ADS  Google Scholar  * Chen, L. Q. Phase-field models for microstructure evolution. _Annu. Rev. Mater. Res._ 32,

113–140 (2002). Article  Google Scholar  * Koduru, R. et al. Phase-field simulations of polarization variations in polycrystalline Hf0.5Zr0.5O2 based MFIM: voltage dependence and dynamics.

_J. Appl. Phys._ 134, 084104 (2023). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported financially by the National Natural Science Foundation of

China (Grant no. 52372100), and the National Key Research and Development Program of China (Grant no. 2019YFA0307900). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Advanced Research

Institute of Multidisciplinary Science, Beijing Institute of Technology, Beijing, 100081, China Zhaobo Liu, Xiaoming Shi, Jing Wang & Houbing Huang * School of Materials Science and

Engineering, Beijing Institute of Technology, Beijing, 100081, China Zhaobo Liu, Xiaoming Shi, Jing Wang & Houbing Huang * Department of Physics, University of Science and Technology

Beijing, Beijing, 100083, China Xiaoming Shi Authors * Zhaobo Liu View author publications You can also search for this author inPubMed Google Scholar * Xiaoming Shi View author publications

You can also search for this author inPubMed Google Scholar * Jing Wang View author publications You can also search for this author inPubMed Google Scholar * Houbing Huang View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Z.L. and H.H. contributed to the design of this study, in the acquisition and interpretation of the

supporting data, and the drafting of the text. X.S. and J.W. contributed to the writing and data interpretation. CORRESPONDING AUTHOR Correspondence to Houbing Huang. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps

and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIALS RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Liu, Z., Shi, X., Wang, J. _et al._ Electric-field-induced crystallization of

Hf0.5Zr0.5O2 thin film based on phase-field modeling. _npj Quantum Mater._ 9, 44 (2024). https://doi.org/10.1038/s41535-024-00652-4 Download citation * Received: 02 January 2024 * Accepted:

20 April 2024 * Published: 23 May 2024 * DOI: https://doi.org/10.1038/s41535-024-00652-4 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative