News Reader.info

ABSTRACT We study the transport properties of underdoped trilayer cuprate HgBa2Ca2Cu3O8+_δ_ with doping level _p_ = 0.10–0.12 in magnetic field up to 88 T. We report for the first time in a

cuprate superconductor a dramatic change of the quantum oscillation spectrum versus temperature, which is accompanied by a sign change of the Hall effect below _T_ ≈10 K. Based on numerical

simulations, we infer a Fermi surface reconstruction in the inner plane from an antiferromagnetic state (hole pockets) to a biaxial charge density wave state (electron pockets). We show that

both orders compete and share the same hotspots of the Fermi surface, and we discuss our result in the context of spin-fermion models. SIMILAR CONTENT BEING VIEWED BY OTHERS PAIR DENSITY

WAVE AT HIGH MAGNETIC FIELDS IN CUPRATES WITH CHARGE AND SPIN ORDERS Article Open access 03 July 2020 CHARGE DENSITY WAVES IN CUPRATE SUPERCONDUCTORS BEYOND THE CRITICAL DOPING Article Open

access 19 March 2021 CHARGE DENSITY WAVES AND FERMI SURFACE RECONSTRUCTION IN THE CLEAN OVERDOPED CUPRATE SUPERCONDUCTOR TL2BA2CUO6+_Δ_ Article Open access 28 January 2022 INTRODUCTION One

of the surprising features of cuprate superconductors is the ubiquity of the interplay between antiferromagnetic (AFM) order, charge density waves (CDWs), and superconductivity1. In general,

these orders compete, and each occupies its own piece of the phase diagram; however, significant coexistence regimes are observed, and these can lead to novel cooperative behavior. For

example, incommensurate CDW and spin orders coexist as magnetic stripes in the La-based cuprates2,3. In other cuprates, CDWs are nonmagnetic, and there have been ongoing efforts to

understand their connection to the strong electron correlations, low dimensionality, and AFM fluctuations that are hallmarks of the cuprates1. The Peierls paradigm that requires extended

sections of Fermi surface to be nested by some wavevector Q, leading to a peak in the non-interacting charge susceptibility, is certainly not at the origin of the cuprate CDWs. There are

other CDW materials without obvious Fermi surface nesting—for example, layered dichalcogenides such as NbSe24 and nonmagnetic pnictides in the BaNi2As2 family5—for which there is compelling

evidence that the CDWs are phonon-driven6,7,8,9. The corresponding evidence in the cuprates is weak10. As an alternative to phonons, spin fluctuations provide a natural mechanism for CDW

formation in cuprates. The mechanism for cuprate superconductivity is widely accepted to be of magnetic origin11, and several analytical calculations predict that spin-fluctuation-mediated

CDWs degenerate with superconductivity at the AFM quantum critical point (where the Néel temperature vanishes)12,13,14,15. This is important because it provides a route to charge order at

high temperatures without Fermi surface nesting. Instead, CDW wavevectors connect Fermi surface “hotspots” that are determined by the Q-dependence of the spin susceptibility. Early versions

of the theory incorrectly predicted that the CDW Q-vectors lie along the Brillouin zone diagonals, with Q = (_q_, ± _q_); however, quantitatively correct axial CDW wavevectors, Q = (_q_, 0),

(0, _q_), are obtained when the dominant diagonal-Q instability is suppressed. This occurs close to the AFM quantum critical point16,17,18, within AFM19,20 or loop-current21 phases, or when

strong correlations are accounted for (see refs. 22,23,24,25). Note, however, that realistic band structures produce weak peaks in the bare charge susceptibility with similar Q-vectors26

despite the lack of proper Fermi surface nesting. Thus, while there is experimental support for Fermi surface hotspots27, it is unresolved whether they are selected by the Fermi surface or

the interaction. CDWs have clear signatures in the transport properties of YBa2Cu3O6+x (YBCO) and single-layer HgBa2CuO4+_δ_ (Hg1201). At low temperatures, the observation of small-frequency

quantum oscillations28,29 combined with negative Hall30,31,32 and Seebeck32,33,34 coefficients indicate the presence of a closed electron pocket in the reconstructed Fermi surface. Details

of the reconstruction are still debated35, but a plausible scenario is a biaxial charge order that creates a small electron-like pocket located at the nodes. Quantum oscillations with small

frequencies have also been observed in the underdoped trilayer cuprate HgBa2Ca2Cu3O8+_δ_ (Hg1223) at hole doping _p_ = 0.08–0.09 but without a sign change in the Hall coefficient down to the

lowest temperatures36. A plausible interpretation is the coexistence of an AFM order in the inner plane and CDW in the outer planes. Multilayer cuprates, with three or more CuO2 layers per

unit cell, offer a new twist on the story because a single material can host distinct phases in different layers simultaneously37. This raises intriguing questions about the coexistence and

competition between these phases, and the possible emergence of novel cooperative phases. In particular, symmetry-inequivalent CuO2 planes differ both in doping and disorder

levels37,38,39,40. In addition, AFM order is more robust in multilayer cuprates and persists up to higher doping as the number of CuO2 planes increases37. RESULTS HALL EFFECT MEASUREMENTS

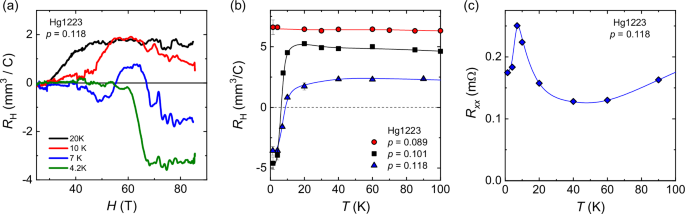
Figure 1a shows the Hall coefficient plotted as a function of magnetic field _H_ for Hg1223 _p_ = 0.118 at different temperatures from _T_ = 20 K down to _T_ = 4.2 K. While _R__H_ is

positive above _T_ = 20 K, it becomes negative at _T_ = 4.2 K and flattens at fields above _H_ ≈70 T, which indicates that the normal state is reached. The temperature-dependence of the

normal-state Hall coefficient measured at the highest fields (see Supplementary Note 5) between _T_ = 1.5 K and 100 K is shown in Fig. 1b at three doping levels, _p_ = 0.118 and _p_ = 0.101

(this work) and _p_ = 0.08936. For _p_ = 0.118 and _p_ = 0.101, there is a sudden sign change of the Hall coefficient below _T_ ≈10 K that is not observed at lower doping. The sign change is

accompanied by a maximum of the resistance at _T_ ≈10 K (see Fig. 1c for _p_ = 0.118). In other cuprates, notably underdoped YBCO41,42,43 and Hg120144,45, this behavior is attributed to the

emergence of charge order. Here, both the abruptness of the transition and its low temperature, are surprising. QUANTUM OSCILLATION MEASUREMENTS Because of the low temperatures, we are in

the rare situation of being able to track the Fermi surface morphology through the CDW transition using quantum oscillation measurements. Figure 2a shows the variation of the tunnel diode

oscillator (TDO) circuit frequency as a function of the magnetic field at different temperatures for the _p_ = 0.112 sample (see Methods). A smooth background subtraction leads to the

oscillatory part of the signal depicted in Fig. 2b. At _T_ = 4.2 K, there is a strong low-frequency oscillation whose amplitude decreases with decreasing temperature. By _T_ = 1.75 K, the

low-frequency oscillations are weak, and small amplitude oscillations at higher frequencies have emerged. This is inconsistent with the Lifshitz–Kosevich theory for a temperature-independent

Fermi surface46, but rather signals a Fermi surface reconstruction. The temperature evolution of the oscillation spectrum is clearly seen in the Fourier analysis of the oscillatory part of

the data (Fig. 2c). At _T_ = 4.2 K, the spectrum is dominated by a low-frequency peak (_F_ = 680 T, black arrow) and its first harmonic. The low-frequency peak weakens and shifts to a higher

frequency (_F_ = 830 T) as the temperature decreases. Two peaks at high frequency, _F_ = 2100 T and _F_ = 2800 T (red arrow), emerge at the lowest temperatures. While the high frequencies

could result from a large effective mass (a Lifshitz–Kosevich analysis for _F_ = 2800 T would have given _m_* = 6.3 ± 0.5 _m__e_, see Supplementary Fig. 6), the Fermi surface reconstruction

scenario is required by the _T_-dependence of the low-frequency oscillation. Note that the evolution of the quantum oscillation spectrum versus temperature has been reproduced in another

sample at doping level _p_ = 0.102 (see Supplementary Fig. 7 and Notes 6). The comparison of quantum oscillations in Hg1223 at different doping levels from _p_ = 0.080 to _p_ = 0.112 is

shown in Supplementary Fig. 8. THEORY Our results demonstrate that a crossover takes place at low temperatures for _p_ = 0.10–0.12 when superconductivity is quenched by a magnetic field. To

gain insight, we numerically simulated quantum oscillations of the density of states for a single CuO2 trilayer. Since the detailed band structure of underdoped Hg1223 is unknown, the

trilayer model was adapted from existing tight-binding models for related multilayer compounds (see Supplementary Note 1). A layer-dependent quasiparticle scattering rate, which modifies QO

amplitudes but not frequencies, was incorporated. We then introduced, by hand, commensurate AFM and CDW order parameters. The AFM and CDW magnitudes, and the CDW periodicity, are the main

tuning parameters in our model, and they were adjusted to give plausible oscillation spectra at each temperature. We found that CDW order alone is insufficient, but that the addition of AFM

order in the inner layer explains the measured oscillations. The required AFM order parameter, _M_ ≲ 50 meV, is small compared to the values _M_ ≳ 100 meV inferred from experiments at

slightly smaller doping36,39. Consistent with this substantial change of energy scales, NMR experiments on related multilayer cuprates37 find that the Néel temperature collapses rapidly near

the end of the metallic AFM phase. Taken together, these suggest that the current doping is close to the AFM quantum critical point. We introduce CDW order parameters Δ_i_ and Δ_o_ for the

inner and outer layers, respectively. The CDWs are biaxial, with wavevectors of magnitude _q_ = 2_π_/4.5_a_0, and with a bond-centered _d_-wave form factor. The true form factor is more

complex47, but would not change our results qualitatively. Similarly, the calculated QOs are not strongly dependent on the value of Δ_o_, which we cannot therefore establish reliably.

Conversely, our results are highly sensitive to both _q_ and Δ_i_. We include scattering rates _Γ__o_,K and _Γ__i_,K for the outer and inner layers, respectively. We assume that _Γ__o_,K is

impurity-dominated, and, therefore, isotropic and _T_-independent, while _Γ__i_,K is anisotropic—either due to pseudogap physics or to order parameter fluctuations—and decreases with

decreasing _T_. The density of states, _N_0(_H_), is obtained at the Fermi energy as a function of magnetic field using a numerical recursion method for large supercells (see Supplementary

Note 2), for the parameters in Table 1. Figure 3a shows that the oscillations at 4.2 K are dominated by a single frequency, while multiple frequencies are evident at 1.8 K. Fourier

transforming with respect to 1/_H_ reveals a strong low-frequency peak at _F_ ≈600 T at 4.2 K, along with harmonics at 1200 and 1800 T [Fig. 3b]. The peak weakens and shifts to a higher

frequency, _F_ ≈800 T, at 1.8 K. Additional peaks, most notably at 1100 and 2700 T, emerge at low _T_. These frequencies agree surprisingly well with the experiments. The reconstructed Fermi

surfaces are too complicated to provide a semiclassical explanation of the peaks (see Fig. 1 of the Supplementary Information). Simplified Fermi surfaces [Fig. 3c, d)] show that the main

peak at 4.2 K comes from hole pockets (blue) generated by AFM order; the other Fermi surfaces (solid red and green) are unchanged by AFM because they have primarily outer-layer character,

but are reconstructed by the outer-layer CDW to form electron pockets (dashed red and green). By assumption, the inner-layer order parameters _M_ and Δ_i_ depend on _T_. Consequently, the

main peak’s frequency increases between 4.2 K and 1.8 K because the hole pocket area grows as _M_ decreases; the peak’s height decreases because of increased quasiparticle scattering by the

CDW (Δ_i_ grows as _T_ decreases) and magnetic breakdown when _M_ is small. Ultimately, Δ_i_ reconstructs the hole pocket at low _T_ to form a diamond-shaped electron pocket [dashed blue in

Fig. 3d] with frequency, _F_ ~2700 T. This provides an explanation for the high-frequency peak seen experimentally [Fig. 2c]. Other low-_T_ peaks in Fig. 3b, at 1100 and 2100 T, are clearly

tied to the growth of Δ_i_, but are difficult to ascribe to a single semiclassical orbit. DISCUSSION Our calculations support the scenario shown in Fig. 4. Above 10 K, inner-layer AFM order

coexists with short-range outer-layer CDW order. Below 10 K, the CDW is sufficiently long-range that the outer-layer Fermi surfaces are reconstructed and generate an electron-like Hall

coefficient; however, the relatively large quasiparticle scattering rate in the outer layers damps the corresponding quantum oscillations. (In our simulations, the outer layers account for

less than 10% of oscillation amplitude.) Though centered on different layers, the AFM and CDW orders compete because the layers are coupled, and the CDW order gradually replaces the AFM

order on the inner layer. In our simulations, the shifts of the main peak height and frequency, and the appearance of a high-frequency peak are intimately connected to this crossover. While

zero-field charge order was detected in Hg122348, we cannot exclude that it is enhanced by the magnetic field, as in YBCO49. The results reported here have a remarkable implication. In our

simulations, the CDW wavevector _q_ was chosen to explain the low-_T_ oscillation peak at ~2800 T. The CDW hotspots implied by this _q_-value are, within the resolution of our simulations,

coincident with the AFM hotspots, i.e., points on the Fermi surface connected by the AFM wavevector \({\bf{Q}}=(\frac{\pi }{{a}_{0}},\frac{\pi }{{a}_{0}})\) (Fig. 4 bottom). This coincidence

is a key feature of models in which CDW order is mediated by critical spin fluctuations carrying momentum Q. In contrast, the CDW order tends to connect points away from the AFM hotspots

when it emerges on top of a pre-existing AFM state20,50. As discussed above, we infer from our measurements that the AFM quantum critical point is nearby. Our measurements are thus

suggestive that charge order at this doping level is mediated by critical spin fluctuations. One possible counter-argument is that the superconducting and long-range CDW transition

temperatures differ by an order of magnitude, contrary to early calculations suggesting they should be the same at the AFM quantum critical point13,14; however, more recent work showed that

the predicted degeneracy breaks down when the band structure lacks particle-hole symmetry19, as in Hg1223. Another possible counter-argument is that CDW order persists in YBCO51, in

La2−xSrxCuO452, and in overdoped Tl2Ba2CuO6+_δ_53 to doping levels far from the AFM quantum critical point. It is unlikely that the AFM hotspot picture makes sense in these doping regimes,

and other (noncritical) interactions are likely important. The question posed by our work is whether the hotspot picture makes sense close to the AFM quantum critical point. In this regard,

it would be interesting to determine the evolution of the CDW wavevectors with doping because the CDW hotspots should be pinned to the AFM Brillouin zone boundary wherever critical spin

fluctuations are the dominant interaction. The fact that the CDW and AFM Fermi surface hotspots coincide in our simulations provides a natural explanation for the competition between the two

phases: both phases derive part of their condensation energy from the gap they open at the hotspot and the phase with the largest condensation energy will form preferentially. Our model

suggests that these energies must be roughly equal at 4.2 K, and that there is growth of the outer-layer CDW below 4.2 K that tips the balance in the inner layer toward the CDW phase. Since

the order parameters reported in Table 1 are directly related to the hotspot gaps, it is tempting to make naive statements about the energetics of the competition between the CDW and AFM

phases. Noting that the _d_-wave character of the CDW means that the CDW gap near the antinode is roughly twice the value shown in the table, and that Δ_o_ is not well-established by our

simulations and could be significantly larger, it is plausible that the AFM and CDW phases have similar gap magnitudes. However, these arguments miss the important point that the CDW and AFM

condensation energies have distinct dependencies on the Fermi surface geometry (unlike BCS superconductors, which depend only on the density of states). Simple arguments about the

energetics of the two phases are, therefore, not possible, and a proper microscopic calculation is required. In conclusion, we have measured the evolution of the Fermi surface at low

temperatures in Hg1223 samples with _p_ = 0.10–0.12, and demonstrated that there is a Fermi surface reconstruction at low temperature. Through numerical simulations, we attribute this to

competition between CDW and AFM order. The CDW wavevectors required to reproduce the experimental oscillation spectrum suggest that the CDW and AFM phases share Fermi surface hotspots. This

naturally explains the competition between the two phases, but is also a hallmark of CDWs that are mediated by critical spin fluctuations. METHODS SAMPLES Single crystals of the trilayer

cuprate HgBa2Ca2Cu3O8+_δ_ have been synthesized using a self-flux growth technique as described in ref. 54. Using adequate heat treatment, Hg1223 can be largely underdoped and its doping

level controlled. The doping _p_ has been deduced from the empirical relation 1 − _T__c_/_T__c_,max = 82.6(_p_−0.16)2, where _T__c_ is the onset superconducting transition measured by SQUID

(see Supplementary Fig. 3) and _T__c_,max = 133 K. The list of samples studied by transport or TDO are shown in Table 2 with their _T__c_ and corresponding hole doping. The results for the

lowest doping _p_ = 0.089 are from ref. 36. TDO MEASUREMENTS Quantum oscillation measurements using the tunnel diode oscillator technique55,56 were performed at the pulsed-field facility in

Toulouse (LNCMI-T) up to 88 T in two samples of Hg1223 at doping levels _p_ = 0.102 (_T__c_ = 96 K) and _p_ = 0.112 (_T__c_ = 108 K). Typical sample dimensions are 500 × 500 × 100 μm3. The

experimental setup consists of an LC-tank circuit powered by a tunneling diode oscillator biased in the negative resistance region of the current-voltage characteristic. The sample is placed

in a compensated 8-shape coil (the diameter and length of the coil are adapted for each sample to optimize the filling factor). The fundamental resonant frequency _f_0 of the whole circuit

is about 25 MHz. The RF signal is amplified and demodulated down to a frequency of about 1 MHz using a heterodyne circuit. A high-speed acquisition system is used to digitize the signal. The

data are post-analysed using a software to extract the field dependence of the resonance frequency _f__T__D__O_, which is sensitive to the resistivity through the change in skin depth. HALL

EFFECT MEASUREMENTS The Hall effect was measured at the LNCMI-T in two distinct samples of Hg1223 at similar doping levels, _p_ = 0.101 (_T__c_ = 95 K) and _p_ = 0.118 (_T__c_ = 114 K). The

magnetic field _H_ was applied along the _c_-axis of the tetragonal structure, perpendicular to the CuO2 planes for both field polarities. Data for the sample _p_ = 0.089 is from ref. 36.

Typical sample dimensions are 700 × 400 × 90 μm3. Gold contacts were sputtered onto the surface of the sample before a heat treatment leading to contact resistances of a few ohms at room

temperature and below 1 Ω at low temperature. The measurements were performed up to 86 T in a dual coil magnet using a conventional four-point configuration with a current excitation of ≈5 

mA at a frequency of ≈60 kHz. A high-speed acquisition system was used to digitize the reference signal (current) and the voltage drop across the sample at a frequency of 500 kHz. The data

were post-analyzed with software to perform the phase comparison. CALCULATIONS We numerically simulated quantum oscillations of the density of states for a tight-binding model of a single

CuO2 trilayer using a numerical recursion method for large supercells (see Supplementary Notes 1, 2 for a detailed description). DATA AVAILABILITY The data that support the findings of this

study are available from the corresponding authors upon reasonable request. CODE AVAILABILITY The codes used during the current study are available from the corresponding author on

reasonable request. REFERENCES * Keimer, B., Kivelson, S., Norman, M., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. _Nature_ 518,

179–186 (2015). Article  ADS  Google Scholar  * Frano, A., Blanco-Canosa, S., Keimer, B. & Birgeneau, R. J. Charge ordering in superconducting copper oxides. _J. Phys. Condens. Matter_

32, 374005 (2020). Article  Google Scholar  * Uchida, S. Ubiquitous charge order correlations in high-temperature superconducting cuprates. _J. Phys. Soc. Jpn._ 90, 111001 (2021). Article 

ADS  Google Scholar  * Zhu, X., Guo, J., Zhang, J. & Plummer, E. W. Misconceptions associated with the origin of charge density waves. _Adv. Phys. X_ 2, 622–640 (2017). Google Scholar  *

Lee, S. et al. Unconventional charge density wave order in the pnictide superconductor Ba(Ni1−_x_Co_x_)2As2. _Phys. Rev. Lett._ 122, 147601 (2019). Article  ADS  Google Scholar  * Johannes,

M. D. & Mazin, I. I. Fermi surface nesting and the origin of charge density waves in metals. _Phys. Rev. B_ 77, 433 (2008). Article  Google Scholar  * Weber, F. et al. Optical phonons

and the soft mode in 2H-NbSe2. _Phys. Rev. B_ 87, 245111 (2013). Article  ADS  Google Scholar  * Souliou, S. et al. Soft-phonon and charge-density-wave formation in nematic BaNi2As2. _Phys.

Rev. Lett._ 129, 247602 (2022). Article  ADS  Google Scholar  * Song, Y. et al. Phonon softening and slowing-down of charge density wave fluctuations in BaNi2As2. _Phys. Rev. B_ 107, L041113

(2023). Article  ADS  Google Scholar  * Souliou, S.-M. et al. In-plane isotropy of the low energy phonon anomalies in YBaCu3O6+_x_. _J. Phys. Soc. Jpn._ 90, 111006 (2021). Article  ADS 

Google Scholar  * Scalapino, D. J. A common thread: the pairing interaction for unconventional superconductors. _Rev. Mod. Phys._ 84, 1383–1417 (2012). Article  ADS  Google Scholar  *

Metlitski, M. & Sachdev, S. Quantum phase transitions of metals in two spatial dimensions. II. Spin density wave order. _Phys. Rev. B_ 82, 075128 (2010). Article  ADS  Google Scholar  *

Metlitski, M. & Sachdev, S. Instabilities near the onset of spin density wave order in metals. _New J Phys._ 12, 105007 (2010). Article  Google Scholar  * Efetov, K. B., Meier, H. &

Pépin, C. Pseudogap state near a quantum critical point. _Nat. Phys._ 9, 442–446 (2013). Article  Google Scholar  * Wang, Y. & Chubukov, A. Charge-density-wave order with momentum (2_q_,

0) and (0, 2_q_) within the spin-fermion model: continuous and discrete symmetry breaking, preemptive composite order, and relation to pseudogap in hole-doped cuprates. _Phys. Rev. B_ 90,

035149 (2014). Article  ADS  Google Scholar  * Pépin, C., Carvalho, V. S. D., Kloss, T. & Montiel, X. Pseudogap, charge order, and pairing density wave at the hot spots in cuprate

superconductors. _Phys. Rev. B_ 90, 195207 (2014). Article  ADS  Google Scholar  * Allais, A., Bauer, J. & Sachdev, S. Density wave instabilities in a correlated two-dimensional metal.

_Phys. Rev. B_ 90, 155114 (2014). Article  ADS  Google Scholar  * Tsuchiizu, M., Yamakawa, Y. & Kontani, H. _p_-Orbital density wave with _d_ symmetry in high-_T_c cuprate

superconductors. _Phys. Rev. B_ 93, 155148 (2016). Article  ADS  Google Scholar  * Wang, X., Wang, Y., Schattner, Y., Berg, E. & Fernandes, R. M. Fragility of charge order near an

antiferromagnetic quantum critical point. _Phys. Rev. Lett._ 120, 247002 (2018). Article  ADS  Google Scholar  * Atkinson, W. A., Kampf, A. P. & Bulut, S. Charge order in the pseudogap

phase of cuprate superconductors. _N. J. Phys._ 17, 013025 (2015). Article  Google Scholar  * Atkinson, W. A., Kampf, A. P. & Bulut, S. Emergence of charge order in a staggered

loop-current phase of cuprate high-temperature superconductors. _Phys. Rev. B_ 93, 134517 (2016). Article  ADS  Google Scholar  * Chowdhury, D. & Sachdev, S. Density-wave instabilities

of fractionalized fermi liquids. _Phys. Rev. B_ 90, 245136 (2014). Article  ADS  Google Scholar  * Banerjee, S., Atkinson, W. & Kampf, A. P. Emergent charge order from correlated

electron-phonon physics in cuprates. _Commun. Phys._ 3, 161 (2020). Article  Google Scholar  * Banerjee, A., Pépin, C. & Ghosal, A. Charge, bond, and pair density wave orders in a

strongly correlated system. _Phys. Rev. B_ 105, 134505 (2022). Article  ADS  Google Scholar  * Mascot, E. et al. Electronic spectra with paramagnon fractionalization in the single-band

Hubbard model. _Phys. Rev. B_ 105, 075146 (2022). Article  ADS  Google Scholar  * Sachdev, S. & La Placa, R. Bond order in two-dimensional metals with antiferromagnetic exchange

interactions. _Phys. Rev. Lett._ 111, 027202 (2013). Article  ADS  Google Scholar  * Atkinson, W. A., Ufkes, S. & Kampf, A. P. Structure of the charge density wave in cuprate

superconductors: lessons from NMR. _Phys. Rev. B_ 97, 125147 (2018). Article  ADS  Google Scholar  * Doiron-Leyraud, N. et al. Quantum oscillations and the fermi surface in an underdoped

high-t c superconductor. _Nature_ 447, 565–568 (2007). Article  ADS  Google Scholar  * Barišić, N. et al. Universal quantum oscillations in the underdoped cuprate superconductors. _Nat.

Phys._ 9, 761–764 (2013). Article  Google Scholar  * LeBoeuf, D. et al. Electron pockets in the fermi surface of hole-doped high-Tc superconductors. _Nature_ 450, 533–536 (2007). Article 

ADS  Google Scholar  * LeBoeuf, D. et al. Lifshitz critical point in the cuprate superconductor YBa2Cu3Oy from high-field hall effect measurements. _Phys. Rev. B_ 83, 054506 (2011). Article

  ADS  Google Scholar  * Doiron-Leyraud, N. et al. Hall, Seebeck, and nernst coefficients of underdoped HgBa2CuO4+_δ_: Fermi-surface reconstruction in an archetypal cuprate superconductor.

_Phys. Rev. X_ 3, 021019 (2013). Google Scholar  * Chang, J. et al. Nernst and seebeck coefficients of the cuprate superconductor YBa2Cu3O6.67: a study of fermi surface reconstruction.

_Phys. Rev. Lett._ 104, 057005 (2010). Article  ADS  Google Scholar  * Laliberté, F. et al. Fermi-surface reconstruction by stripe order in cuprate superconductors. _Nat. Commun._ 2, 432

(2011). Article  ADS  Google Scholar  * Proust, C. & Taillefer, L. The remarkable underlying ground states of cuprate superconductors. _Ann. Rev. Cond. Matt. Phys._ 10, 409–429 (2019).

Article  ADS  Google Scholar  * Oliviero, V. et al. Magnetotransport signatures of antiferromagnetism coexisting with charge order in the trilayer cuprate HgBa2Ca2Cu3O8+_δ_. _Nat. Commun._

13, 1568 (2022). Article  ADS  MathSciNet  Google Scholar  * Mukuda, H., Shimizu, S., Iyo, A. & Kitaoka, Y. High-Tc superconductivity and antiferromagnetism in multilayered copper

oxides: a new paradigm of superconducting mechanism. _J. Phys. Soc. Jpn._ 81, 011008 (2012). Article  ADS  Google Scholar  * Ideta, S. et al. Enhanced superconducting gaps in the trilayer

high-temperature Bi2Sr2Ca2Cu3O10+_δ_ cuprate superconductor. _Phys. Rev. Lett._ 104, 227001 (2010). Article  ADS  Google Scholar  * Kunisada, S. et al. Observation of small fermi pockets

protected by clean CuO2 sheets of a high-_T__c_ superconductor. _Science_ 369, 833–838 (2020). Article  ADS  Google Scholar  * Luo, X. et al. Electronic origin of high-_T__c_ maximization

and persistence in trilayer cuprate superconductors. _Nature Phys._ 13, 1841–1847 (2023). Article  ADS  Google Scholar  * Wu, T. et al. Magnetic-field-induced charge-stripe order in the

high-temperature superconductor YBa2Cu3O_y_. _Nature_ 477, 191–194 (2011). Article  ADS  Google Scholar  * Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in

(Y,Nd)Ba2Cu3O6+_x_. _Science_ 337, 821–825 (2012). Article  ADS  Google Scholar  * Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order

in YBa2Cu3O6.67. _Nat. Phys._ 8, 871–876 (2012). Article  Google Scholar  * Tabis, W. et al. Charge order and its connection with fermi-liquid charge transport in a pristine high-_T__c_

cuprate. _Nat. Commun._ 5, 5875–5880 (2014). Article  ADS  Google Scholar  * Chan, M. K. et al. Extent of fermi-surface reconstruction in the high-temperature superconductor HgBa2CuO4+_δ_.

_Proc. Natl Acad. Sci. USA_ 117, 9782–9786 (2020). Article  ADS  Google Scholar  * Shoenberg, D. _Magnetic Oscillations in Metals_ (Cambridge Univ. Press, 1984). * McMahon, C. et al. Orbital

symmetries of charge density wave order in YBa2Cu3O6+_x_. _Sci. Adv._ 6, eaay0345 (2020). Article  ADS  Google Scholar  * Loret, B. et al. Intimate link between charge density wave,

pseudogap and superconducting energy scales in cuprates. _Nat. Phys._ 15, 771–775 (2019). Article  Google Scholar  * Gerber, S. et al. Three-dimensional charge density wave order in

YBa2Cu3O6.67 at high magnetic fields. _Science_ 350, 949–952 (2015). Article  Google Scholar  * Harrison, N. Robustness of the biaxial charge density wave reconstructed electron pocket

against short-range spatial antiferromagnetic fluctuations. _Phys. Rev. B_ 97, 245150 (2018). Article  ADS  Google Scholar  * Blanco-Canosa, S. et al. Resonant x-ray scattering study of

charge-density wave correlations in YBa2Cu3O6+_x_. _Phys. Rev. B_ 90, 054513 (2014). Article  ADS  Google Scholar  * Wen, J.-J. et al. Observation of two types of charge-density-wave orders

in superconducting La2-xSrxCuO4. _Nat. Commun._ 10, 3269 (2019). Article  ADS  Google Scholar  * Tam, C. C. et al. Charge density waves and Fermi surface reconstruction in the clean

overdoped cuprate superconductor Tl2Ba2CuO6+_δ_. _Nat. Commun._ 13, 570 (2022). Article  ADS  Google Scholar  * Loret, B. et al. Crystal growth and characterization of HgBa2Ca2Cu3O8+_δ_

superconductors with the highest critical temperature at ambient pressure. _Inorg. Chem._ 56, 9396–9399 (2017). Article  Google Scholar  * Coffey, T. et al. Measuring radio frequency

properties of materials in pulsed magnetic fields with a tunnel diode oscillator. _Rev. Sci. Instrum._ 71, 4600–4606 (2000). Article  ADS  Google Scholar  * Drigo, L., Durantel, F.,

Audouard, A. & Ballon, G. Tunnel diode oscillator-based measurement of quantum oscillations amplitude in pulsed high magnetic fields: a quantitative field-dependent study. _Eur. Phys. J.

Appl. Phys._ 52, 10401 (2010). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS W.A.A. acknowledges the support of the Natural Sciences and Engineering Research Council of

Canada (NSERC). This work was made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (www.sharcnet.ca) and the Digital Research Alliance of Canada.

D.V., D.C., and C.P. acknowledge support from the EUR grant NanoX noANR-17-EURE-0009 and from the ANR grant NEPTUN noANR-19-CE30-0019-01. This work was supported by LNCMI-CNRS, members of

the European Magnetic Field Laboratory (EMFL). AUTHOR INFORMATION Author notes * S. Benhabib Present address: Laboratoire de Physique des Solides, 91405, Orsay, France * These authors

contributed equally: V. Oliviero, I. Gilmutdinov. AUTHORS AND AFFILIATIONS * LNCMI-EMFL, CNRS UPR3228, Univ. Grenoble Alpes, Univ. Toulouse, INSA-T, Grenoble and Toulouse, Toulouse, France

V. Oliviero, I. Gilmutdinov, D. Vignolles, S. Benhabib, N. Bruyant & C. Proust * Service de Physique de l’Etat Condensé, CEA Saclay (CNRS-URA 2464), Gif sur Yvette, 91191, France A.

Forget & D. Colson * Department of Physics and Astronomy, Trent University, Peterborough, K9L 0G2, ON, Canada W. A. Atkinson Authors * V. Oliviero View author publications You can also

search for this author inPubMed Google Scholar * I. Gilmutdinov View author publications You can also search for this author inPubMed Google Scholar * D. Vignolles View author publications

You can also search for this author inPubMed Google Scholar * S. Benhabib View author publications You can also search for this author inPubMed Google Scholar * N. Bruyant View author

publications You can also search for this author inPubMed Google Scholar * A. Forget View author publications You can also search for this author inPubMed Google Scholar * D. Colson View

author publications You can also search for this author inPubMed Google Scholar * W. A. Atkinson View author publications You can also search for this author inPubMed Google Scholar * C.

Proust View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS V.O., S.B., N.B., D.V., and C.P. performed the TDO measurements. I.G., V.O., D.V.,

and C.P. performed the Hall effect measurements. W.A.A. performed the calculations. A.F. and D.C. grew, annealed the single crystals, and performed SQUID measurements. W.A.A. and C.P.

supervised the project and wrote the manuscript with inputs from all the authors. CORRESPONDING AUTHORS Correspondence to W. A. Atkinson or C. Proust. ETHICS DECLARATIONS COMPETING INTERESTS

The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTAL INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives

4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted

material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise

in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the

permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Oliviero, V., Gilmutdinov, I., Vignolles, D. _et al._ Charge order near the antiferromagnetic quantum critical point in the trilayer high

_T__c_ cuprate HgBa2Ca2Cu3O8+_δ_. _npj Quantum Mater._ 9, 75 (2024). https://doi.org/10.1038/s41535-024-00688-6 Download citation * Received: 20 June 2024 * Accepted: 22 September 2024 *

Published: 04 October 2024 * DOI: https://doi.org/10.1038/s41535-024-00688-6 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link

Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative