News Reader.info

ABSTRACT Understanding and manipulating cell fate determination is pivotal in biology. Cell fate is determined by intricate and nonlinear interactions among molecules, making mathematical

model-based quantitative analysis indispensable for its elucidation. Nevertheless, obtaining the essential dynamic experimental data for model development has been a significant obstacle.

However, recent advancements in large-scale omics data technology are providing the necessary foundation for developing such models. Based on accumulated experimental evidence, we can

postulate that cell fate is governed by a limited number of core regulatory circuits. Following this concept, we present a conceptual control framework that leverages single-cell RNA-seq

data for dynamic molecular regulatory network modeling, aiming to identify and manipulate core regulatory circuits and their master regulators to drive desired cellular state transitions. We

illustrate the proposed framework by applying it to the reversion of lung cancer cell states, although it is more broadly applicable to understanding and controlling a wide range of

cell-fate determination processes. SIMILAR CONTENT BEING VIEWED BY OTHERS GENE REGULATORY NETWORK INFERENCE DURING CELL FATE DECISIONS BY PERTURBATION STRATEGIES Article Open access 04 March

2025 LANDSCAPE CONTROL FOR CELL FATE TRANSITIONS Article Open access 07 June 2025 NETISCE: A NETWORK-BASED TOOL FOR CELL FATE REPROGRAMMING Article Open access 20 June 2022 INTRODUCTION

Cell-fate determination is an evolutionarily well-conserved process through which cells make critical decisions regarding their ultimate roles within a multicellular organism1. This

foundational process underpins functions that are indispensable for all multicellular organisms, including the precise orchestration of normal developmental pathways, the maintenance of

internal equilibrium (homeostasis), and the facilitation of adult tissue regeneration. Due to its vital importance, cell-fate determination has evolved to be highly resilient to various

perturbations. Nevertheless, seminal experimental findings have revealed that the predetermined destiny of a cell can be dramatically reshaped by a few molecular modifications. For instance,

the overexpression of Yamanaka factors OCT4, SOX2, KLF4, and c-MYC (OSKM)-can reprogram differentiated fibroblasts into induced pluripotent stem cells2. Moreover, ectopic activation of

Yes-associated protein can transdifferentiate terminally differentiated hepatocytes into biliary epithelial-like cells3. In addition, adenomatous polyposis coli restoration is able to

reverse colon carcinoma cells back to a functionally normal state despite the presence of potent oncogenic mutations4. These findings collectively highlight that predisposed cell fates, in

principle, can be changed by manipulating a few specific molecules, called master regulators, while remaining highly robust against most other molecular perturbations. This perspective

further raises the following challenges: how can we identify the master regulators, and through what molecular regulatory mechanisms do they induce cell-fate changes? Cells are dynamic

systems composed of intricate signaling pathways interconnected by various feedbacks and crosstalks, forming a complex network5,6. The regulatory relationships within this network are

predominantly nonlinear, adding layers of complexity that defy simple, intuitive predictions about how altering a specific molecule might impact cellular functions7,8. The inherent

complexity and nonlinearity present significant challenges in understanding the principles underlying cell-fate determination and its control. To comprehend the intricate networks of

intracellular molecular regulations, a systems biology approach that integrates quantitative mathematical modeling with molecular experimentation is indispensable. In this perspective, we

argue that the integration of newly emerging dynamic information with mathematical models enables us to not only decode the fundamental principles embedded in the process of cell-fate

determination, but also to exert control over this intricate process to the degree that was previously unachievable. In particular, we propose that although cell-fate determination

accompanies genome-wide molecular state changes, it might be underpinned by only specific subnetworks within the network, which we refer to as ‘core regulatory circuits’. These circuits are

instrumental in orchestrating the intricate sequence of events that determine cell fate. Based on this, we present a conceptual framework that employs single-cell RNA-sequencing (scRNA-seq)

data to identify and manipulate core regulatory circuits determining cell fate. By applying this framework to scRNA-seq data of tumorigenesis, we propose a system-level approach to identify

molecular candidates for cancer reversion and their molecular mechanisms through which deregulated gene regulatory dynamics are rewired, and cancer hallmarks can be compromised to

reestablish normal phenotypes. REPRESENTING CELL-FATE CHANGES BY COMPLEX MOLECULAR NETWORK DYNAMICS Cellular functions are orchestrated by a gene regulatory network (GRN) composed of tens of

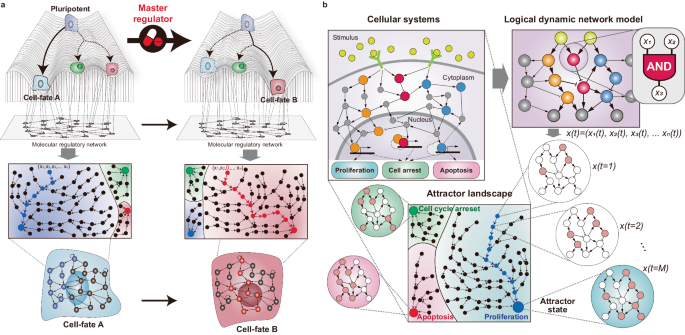
thousands of genes, intertwined through intricate nonlinear interactions. Network dynamics can be conceptualized through Waddington’s landscape, an intuitive model that illustrates how

cells navigate through various states within a high-dimensional state space9 (Fig. 1a). In this landscape, valleys correspond to specific cell types, known as ‘attractors’, representing

stable states that cells naturally settle into10. Building on this, the concept of ‘attractor landscape’ further illustrates the array of potentially stable states that cells can adopt. The

basins surrounding these attractors indicate the probability of cells adopting each phenotype, offering insights into the dynamics and probabilities of cell-fate transitions. In this

context, cell fates can be regarded as the most probable states a cell can occupy within the attractor landscape, reflecting their potential transition trajectories. In principle, the

predetermined cell fates can be changed by altering the attractor landscapes of cells by rewiring the core regulatory circuits that underlie their complex molecular interactions11,12 (Fig.

1a). Can Waddington’s landscape metaphor be used for a quantitative description of actual cell-fate determination? Moreover, can it be applied to cell-fate inference and control? Such a

metaphorical landscape can be quantitatively described through mathematical models (Fig. 1b). These models formalize the state of a cell at time _t_ by the collective value of each molecular

state in the network. For example, a network composed of _n_ genes can be represented at time _t_ by the state vector \({x}(t)=\left({x}_{1}\left(t\right),{x}_{2}\left(t\right),\ldots

,{x}_{n}(t)\right)\). In this vector, \({x}_{i}\left(t\right)\) for \(i\in \left\{\mathrm{1,2},\ldots ,n\right\}\) denotes the state of the _i_th gene at time _t_, and thus, \(x(t)\)

corresponds to a point in an _n_-dimensional gene expression state space. The state of each molecule is influenced by the GRN, where the future state of each molecule is determined by

nonlinear interactions with its upstream molecules. Consequently, a cellular state evolves over time as a nonlinear function of all molecules in the network,

\(x(t+1)={F}\left({x}_{1}\left(t\right),{x}_{2}\left(t\right),\ldots ,{x}_{n}(t)\right)\), converging towards a particular state (or a set of states) in the state space, which is called the

attractor state. Empirical estimation of the network structure and nonlinear function parameters from experimental data is essential for a reasonably accurate model of cell-fate

determination. However, obtaining the dynamic data needed for the estimation has been experimentally challenging. Fortunately, recent advances in single-cell omics and related analytical

technologies can now provide the necessary temporal data required for the construction of comprehensive mathematical models. METHODOLOGIES AVAILABLE TO CONSTRUCT MATHEMATICAL MODELS USING

SINGLE-CELL OMICS DATA Single-cell sequencing technologies are advancing rapidly and are now capable of analyzing datasets, including transcriptomes, epigenomes, and proteomes from hundreds

of thousands of cells. In particular, RNA sequencing has emerged as the leading technique in single-cell omics13. Sequencing RNA at the single-cell level allows for a detailed examination of

gene transcription, providing a high-dimensional fingerprint that identifies unique cellular characteristics. Consequently, scRNA-seq has become an invaluable tool for investigating cell

identity and state transitions at the level of individual cells. In this perspective, we focus on scRNA-seq. We illustrate current methodologies for utilizing scRNA-seq data in studying

cell-fate determination, which encompass several critical stages as summarized below. The initial stage involves preprocessing raw count data (Fig. 2a). This crucial first step, using tools

such as Seurat14, Scanpy15, and Bioconductor-based SingleCellExperiment16, involves rigorous quality control, normalization, and feature selection, to establish a robust foundation for

subsequent analyses. Following preprocessing, the complexity of data is dealt with through dimensionality reduction techniques like PCA17, t-SNE18, and UMAP19, effectively simplifying the

data while preserving its essential characteristics (Fig. 2b). Following dimensionality reduction, clustering algorithms such as Louvain20, Leiden20, DBSCAN21, and SINCERA22 are used to

group cells with shared identities. This step is followed by the annotation of each clustered cell type using established biological knowledge, and the identification of specific cell states

that correlate with the cell fates of interest. To re-order cellular trajectories according to gene expression changes, pseudotime analysis tools like Monocle323 are employed to map cell

trajectories from scRNA-seq snapshots (Fig. 2c). RNA velocity24,25, based on vectors derived from mRNA splicing dynamics, also indicates the direction and likelihood of cell state

transitions. Additional methods like Slingshot26, PAGA27, and FateID28 are also useful for inferring cellular dynamic trajectories and quantifying cell-fate probabilities. The next phase

involves constructing a molecular regulatory network (Fig. 2d, top), which infers molecular interactions from previously processed data29, often utilizing mutual information to understand

nonlinear relationships within transcriptomic data. Tools such as Scribe30 and CLR31, utilize mutual information to gauge nonlinear transcriptomic relationships, and are instrumental in

building the molecular regulatory network. GENIE332, GRNBoost233, PIDC34, LEAP35, and SCENIC36 are also widely used for this purpose. Furthermore, by integrating different single-cell data

modalities (e.g., gene expression, chromatin accessibility), SCENIC+37, Pando38, Dictys39, and CellOracle40 can estimate the regulatory effect of each transcription factor (TF) on each gene

mediated by specific regions of DNA, and then infer the more specific GRN structure. In addition to the constructed GRN structure, mathematical models are constructed by inferring and

encapsulating critical regulatory dynamics from scRNA-seq data (Fig. 2d, bottom). To construct a logical dynamic model, methods such as BTR (BoolTraineR)41 and SCNS (single cell network

synthesis)42 can be employed. Building a Boolean network model requires optimizing Boolean regulation logic. This process is tailored to each algorithm used, such as the Z3 solver and the

Quine-McCluskey (QM) algorithm, and is performed on binarized data to ensure optimal precision. Parallel to this, continuous dynamic modeling adopts a different approach. This method often

involves deriving ordinary differential equations (ODEs) or stochastic differential equations, with a particular emphasis on pseudotime ordering of the data43,44,45. For example, SCODE44

employs linear regression techniques, whereas SCOUP45 utilizes a continuous diffusion process and is designed to analyze single-cell expression data during differentiation processes. This

latter model, based on the Ornstein–Uhlenbeck process, is especially adept at determining the interdependencies between gene expression levels at distinct temporal points. This method offers

a more detailed understanding of cellular dynamics across various time points. To summarize, we provide a brief overview of useful methods for constructing mathematical models (Table 1).

These models are invaluable for identifying molecular targets, particularly master regulators, through extensive systematic perturbation analysis using tools like CellOracle40 and

scTenifoldKnk46, which predict gene perturbation effects and identify key cell-fate regulators (Fig. 2e). However, despite their advanced capabilities, these methods require laborious

processes that involve individually controlling molecules and analyzing complex systems. Furthermore, these tools do not inherently incorporate an understanding of system dynamics, such as

the attractor landscape, into their analyses. This poses significant limitations on revealing the specific molecular regulatory mechanisms that dictate cell-fate decisions. To address these

challenges, control theory may offer a new path forward. EMERGING SIGNIFICANCE OF APPLYING CONTROL THEORY TO EXPLORE CORE REGULATORY CIRCUITS AND THEIR MASTER REGULATORS Control theory is a

field of study that focuses on system characterization and manipulation. It involves understanding how systems behave and devising methods to achieve desired outcomes through control

actions. This discipline has evolved over time to address vital challenges in complex systems. In the early 20th century, Black’s development of the negative feedback amplifier laid the

groundwork for feedback control of simple systems47. In the 21st century, Wolkenhauer, Kitano, and Cho introduced the interdisciplinary principles of systems biology, merging control theory

with high-throughput technologies for cellular research48. Aligned with this evolution, in 2011, Barabási and Slotine made a significant advancement in complex network control by integrating

network science with control theory49. Their works highlighted the future focus on addressing the intricate interplay of elements in a nonlinear, networked system. Current developments in

complex network control theories have evolved in two principal directions: one that focuses on the structural characteristics of networks and another that considers the inherent nonlinear

dynamics within these networks. Controlling network centrality determines the most influential regulators in network interactions using metrics such as degree centrality, betweenness

centrality, and eigenvector centrality50. This approach often aims to identify a minimal subset of driver nodes required to direct a network from any given state to a specific desired

state51. In contrast, strategies for controlling network dynamics, like logical domain of influence (LDOI)52, feedback vertex set (FVS)53, stable motif54, searching for differential

expressed positive circuits (DEPCs)55, and global stabilization analysis56, were suggested to manage state transitions caused by the network dynamics. These methods collectively aim not only

to identify ‘control targets’, defined as a specific set of nodes capable of steering the system towards a set of desired states, but also offer tools for analyzing molecular regulatory

mechanisms. For instance, stable motif analysis has been instrumental in uncovering crucial feedback loops that govern processes like the epithelial-to-mesenchymal transition57, leukemia

cell-fate decisions54, and the differentiation of helper T cells54. In addition, the LDOI approach has identified key control targets and their influences, and the DEPC method has discovered

related positive circuits to stabilize a certain attractor55. While these methods provide solutions for controlling theoretical model systems, some result in suboptimal solutions with

unnecessary targets, and yet others face scalability issues, rendering them limited to very small-scale models. Furthermore, to our knowledge, there has been no attempt to systematically

identify both control targets and the resulting fate-determining paths (or circuits) revealing specific molecular regulatory mechanisms. Thus, identifying optimal control targets (i.e.,

master regulators) and the resulting core regulatory circuits for real-world cell-fate control remains a significant challenge. To address the aforementioned challenge, leveraging the key

biological features that play a role in cell-fate determination could be an essential strategy. Many previous experimental studies have already shown that while cell systems are comprised of

a complex large network, a core regulatory circuit, composed of only a few key molecules, plays a crucial role in determining cell fates58,59,60,61. In particular, such core regulatory

circuits are often composed of multiple nested feedback loops, with at least one being a positive feedback loop. For example, in quorum sensing, molecules like N-acyl homoserine lactone

(AHL) in bacteria facilitate population-wide communication62; the regulatory feedback between TFs OCT4, SOX2, and NANOG maintains pluripotency in embryonic stem cells63; the double negative

feedback loop between PU.1 and GATA1 controls the erythroid versus myeloid lineage commitment64; and the interconnected SNAIL/miR-34 and ZEB/miR-200 feedback loops are key regulatory

components of the epithelial–mesenchymal transition (EMT) process in cancer metastasis65 (Fig. 3a). Furthermore, combinations of feedback and feedforward controls can generate biological

transitions reliably in noisy environments where the activity of individual components can vary over a range of parameters66. Those previous studies indicate the significance of specific

feedback mechanisms within core regulatory circuits in governing crucial cellular processes. This leads to the following question: how can we identify these core regulatory circuits and

their master regulators? To computationally resolve this problem, the concept of a network kernel has been introduced, encompassing the ‘kernel’ method for simplifying networks67 and the

‘control kernel’ approach for altering attractor landscapes with minimal regulators68,69. These kernel-based approaches are crucial for focusing on and controlling the core regulatory

circuits that govern vital biological phenomena. Similarly, since cellular circuits with positive feedback loops induce multistationary behavior, identifying and analyzing the properties of

feedback loops can offer critical clues to determine core regulatory circuits within large networks69,70,71. Another algorithm, ‘OpitCon’, can identify combination targets using a subgraph

based on structural controllability theory, and then describe specific core downstream subnetworks and their crosstalk links that contribute to therapy resistance72. More recently, Rukhlenko

et al.73 developed a novel framework called ‘cSTAR’. This method uses omics data to classify cell states and transforms them into mechanistic models. These models consist of a key molecular

regulatory network that is instrumental in controlling the attractor landscape that governs cell-fate determination. Moreover, systematic perturbation to the model helps to identify control

targets for the desired change in cell fate. Based on previous studies, we postulate that core regulatory circuits consist of subnetworks interconnected by feedback loops, and that these

circuits are the primary drivers of cell fate. Further advancing this concept, we can propose a detailed procedure as follows. First, we can investigate all feedback loops associated with

different cellular states of interest (Fig. 3b). Subsequently, through an analysis of network dynamics influenced by feedback loop states, we can prioritize the positive feedback loops that

are instrumental in controlling the attractor landscape governing cell-fate determination (Fig. 3c). For this, we can employ previous control methods such as LDOI52, stable motif54, and

DEPC55, or improve these methods for further exploration of key subnetworks. As a result, the prioritized feedback loops can be refined to form a core regulatory circuit. Lastly, through

systematic perturbation to the model (or core regulatory circuit) or by employing the improved kernel-based methods, we can identify (minimal) master regulators for the desired cell-fate

change (Fig. 3d). Together, this control theory-based approach would be a highly promising way to understand and manipulate cell-fate processes, centered around core regulatory circuits, of

a dynamic system. From this, we integrate aforementioned progresses and suggest a comprehensive framework for systematically identifying core regulatory circuits and their master regulators

for cell-fate change (Fig. 4). This framework consists of three interconnected components: capturing dynamic information from single-cell omics data, constructing and analyzing a

mathematical model of molecular mechanisms in cell-fate determination, and identifying the candidates of master regulators for a desired cell-fate control (Fig. 4a–c). To explicitly

introduce our framework, we provide an illustrative example as follows. ILLUSTRATIVE EXAMPLE: IDENTIFYING CONTROL TARGETS FOR CANCER REVERSION BY USING SINGLE-CELL RNA-SEQUENCING DATA FROM

LUNG CANCER SAMPLES Traditional anticancer therapies have focused on removing cancer cells, but their effectiveness is limited due to the inevitable emergence of resistance, which arises as

a consequence of cancer cell plasticity. Cancer plasticity is an emerging hallmark of cancer cells, and it plays a crucial role in cancer initiation and progression, as well as adaptation to

therapy and intra-tumoral heterogeneity74,75,76. Hence, recent research has shifted focus towards targeting highly plastic cancer cells emerging during tumorigenesis, aiming to inhibit

their development. This illustrative example shows the emerging concept of ‘cancer reversion’, which seeks to transform highly plastic lung cancer cells back into normal cells, instead of

merely eliminating cancer cells. Recent studies have indicated that cells with high plasticity emerge during mouse lung tumorigenesis upon introduction of KRAS mutations into AT2 cells,

which are typically considered the origin of lung cancer. These cells lose their original characteristics and transition through AT1/AT2-like states, eventually diversifying into various

cancer cell types such as EMT-type, embryonic liver-like, GI-like, and high-cycling cells, thereby increasing tumor heterogeneity (Fig. 5a). In this illustrative example, we begin with

obtaining time-series scRNA-seq data collected during lung tumorigenesis from AT2 cell state to high-plasticity cell state (HPCS) from a public repository77. This dataset provides

single-cell transcriptomic information for ~2200 cells. The proposed framework entails preprocessing, dimensionality reduction, and clustering to annotate cell identities at different stages

during tumorigenesis. Then, it conducts pseudotime ordering to delineate the trajectory from AT2 cells, through intermediate states, to HPCS cells, providing a comprehensive map of cellular

evolution during lung tumorigenesis (Fig. 5b). The proposed framework identifies critical TFs that can regulate gene expression changes along the lung tumorigenesis trajectory by comparing

the activities of TFs among the distinct cell clusters. Then, the interactions among these TFs can be inferred, resulting in a GRN structure consisting of 105 nodes and 304 links (Fig. 5c).

Next, to explore essential regulatory mechanisms associated with specific phenotypes, the framework can investigate all positive feedback loops showing differential activation between AT2

and HPCS states by evaluating their TF activities. By aggregating those feedback loops, the framework generates a reduced GRN, consisting of 23 nodes and 74 links, which contains key

dynamical information (Fig. 5d). Intriguingly, TFs within the same state (e.g., AT2 or HPCS) are primarily interconnected through mutually activating positive feedback, whereas TFs across

distinct states (e.g., AT2 versus HPCS) engage predominantly through mutually inhibitory interactions. With the GRN structure and trajectory information, a Boolean logic model can be

constructed to simulate the tumorigenesis process. This process involves discretizing the continuous expression values of each TF along the pseudotime trajectory (employing clustering

methods like k-means). Subsequently, the influence of each TF in the GRN structure can be determined through Boolean logic functions, utilizing the QM algorithm (Fig. 5e). Using the Boolean

network model, the framework can pinpoint the feedback loops of the most dynamic significance (in this example, stable motifs). These feedback loops and their corresponding LDOIs have the

potential to stabilize either phenotype when modulated. Then the framework can assess the influence of the LDOIs on AT2 and HPCS modules, and prioritize key feedback loops based on their

relevance to either phenotype (Fig. 5f). The most influential feedback loops can form a core regulatory circuit, consisting of Rel, Irf1, Irf7, Fosl1, Myc, and Relb. Once the core regulatory

circuit is stabilized, it can fix the values of most TFs within the respective AT2 and HPCS modules. The proposed framework then leverages information on core regulatory circuits to find

control targets that can inhibit the HPCS module and activate the AT2 module. The LDOIs for individual nodes and pairs of nodes are calculated, then each LDOI is checked whether it can fix

the influential feedback loops in the desired state to identify control targets. For example, a combination of Fosl1 (or Myc) and Nfkb2 can be identified as a master regulator, thereby

ensuring the stable activation of the AT2 module and the deactivation of the HPCS module (Fig. 5g). Inhibition of Fosl1 can deactivate HPCS TF activities while having no impact on AT2 TFs.

On the other hand, disruption of Nfkb2 can de-repress AT2 TF activities in the HPCS state, activating downstream regulators and leading to the re-emergence of the AT2 state. Combined

inhibition of E2f4 and Nfkb2 can destabilize the HPCS state, and enable a stable activation of the AT2 module. This combinatorial inhibition strategy can, therefore, effectively disrupt the

positive feedback within the HPCS module while also neutralizing its negative impact on the AT2 module. The result shows a stable shift from a highly plastic cancerous state back to a

normal-like AT2 state. Moreover, the role of key molecules in plastic cancer cells can be illustrated using the landscape concept (Fig. 5h). In these cells, Fosl1 and Nfkb2 are highly

active, stabilizing the HPCS while repressing the normal AT2 module. This ensures the persistence of the HPCS. However, to revert HPCS back to normal, merely inhibiting either Fosl1 or Nfkb2

is insufficient, as each alone does not fully shift the landscape towards the AT2 phenotype. The positive feedback of Fosl1 maintains the HPCS state, or the remaining activity of Nfkb2

suppresses the AT2 module. Only the simultaneous inhibition of both Fosl1 and Nfkb2 can significantly alter the landscape, favoring a shift towards the AT2 phenotype. In summary, this

example illustrates how systems biology can be applied to understand and manipulate cell-fate transitions in cancer. By integrating mathematical modeling with experimental data, we can

identify crucial regulatory mechanisms that reverse cell states, offering new insights and potential therapeutic strategies in cancer treatment. Although this example illustrates the whole

process proposed for inducing cancer reversion from public single-cell data, limitations are noted. Cell-fate determination is a complex phenomenon that encompasses changes not just at the

transcriptomic level but also across various molecular levels. The continuous development of technologies that utilize single-cell multiomics data, which integrate transcriptomic, proteomic,

and epigenetic data, has been pivotal. The use of such data can significantly enhance the proposed framework. In particular, the recent increase in single-cell multiomics data, combining

scRNA-seq and scATAC-seq, has been noteworthy. scATAC-seq allows for the pruning of indirect regulation information from functional regulatory relationships obtained from transcriptomic data

by providing information on the open chromatin regions at promoter sites. This enables the construction of more accurate GRN structures and, consequently, the development of more precise

mathematical models. Furthermore, factors like the physiological state of a cell, not directly included in omics data, can significantly influence cell fate78. Although our framework does

not directly incorporate such state information, it can be indirectly reflected through TF activity within the GRN structure and its mathematical model. The future availability of

technologies for simultaneous measurement of the physiological and molecular states of a cell promises the development of models that integrate these dimensions for a comprehensive

understanding. CONCLUSIONS Among the various molecules within a cell, only a few key molecules have a significant impact on cell fate. What distinguishes these master regulators from other

molecules? How can we identify those master regulators, and through what molecular regulatory mechanisms do they induce cell-fate changes? To answer these questions, it is necessary to

analyze and understand the behavior of a huge molecular regulatory network within a cell. In the past, such attempts were limited due to experimental constraints. Yet, recent advances in

single-cell omics technologies, along with a decade of progress in network control technologies, enable us to answer these fundamental questions and usher in a renaissance for systems

biology. The conceptual framework we introduce can offer an unprecedented opportunity for cell fate control by integrating the latest technological innovations into a comprehensive, novel

strategy. REFERENCES * Moris, N., Pina, C. & Arias, A. M. Transition states and cell fate decisions in epigenetic landscapes. _Nat. Rev. Genet._ 17, 693–703 (2016). Article  CAS  PubMed

  Google Scholar  * Takahashi, K. & Yamanaka, S. Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures by defined factors. _Cell_ 126, 663–676 (2006).

Article  CAS  PubMed  Google Scholar  * Panciera, T. et al. Induction of expandable tissue-specific stem/progenitor cells through transient expression of YAP/TAZ. _Cell Stem Cell_ 19,

725–737 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Dow, L. E. et al. Apc restoration promotes cellular differentiation and reestablishes crypt homeostasis in colorectal

cancer. _Cell_ 161, 1539–1552 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Shin, S. Y. et al. Functional roles of multiple feedback loops in extracellular signal-regulated

kinase and Wnt signaling pathways that regulate epithelial-mesenchymal transition. _Cancer Res._ 70, 6715–6724 (2010). Article  CAS  PubMed  PubMed Central  Google Scholar  * Hong, J. Y. et

al. Computational modeling of apoptotic signaling pathways induced by cisplatin. _BMC Syst. Biol._ 6, 122 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar  * Park, S. G. et al.

The influence of the signal dynamics of activated form of IKK on NF-kappaB and anti-apoptotic gene expressions: a systems biology approach. _FEBS Lett._ 580, 822–830 (2006). Article  CAS 

PubMed  Google Scholar  * Lee, H. S., Hwang, C. Y., Shin, S. Y., Kwon, K. S. & Cho, K. H. MLK3 is part of a feedback mechanism that regulates different cellular responses to reactive

oxygen species. _Sci. Signal._ 7, ra52 (2014). Article  PubMed  Google Scholar  * Waddington, C. H. The strategy of the genes. (Routledge, 2014). * Wang, J., Zhang, K., Xu, L. & Wang, E.

Quantifying the Waddington landscape and biological paths for development and differentiation. _Proc. Natl. Acad. Sci. USA_ 108, 8257–8262 (2011). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Zhang, J., Nie, Q. & Zhou, T. Revealing dynamic mechanisms of cell fate decisions from single-cell transcriptomic data. _Front. Genet._ 10, 1280 (2019). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Joo, J. I., Zhou, J. X., Huang, S. & Cho, K.-H. Determining relative dynamic stability of cell states using boolean network model. _Sci. Rep._

8, 12077 (2018). Article  PubMed  PubMed Central  Google Scholar  * Hwang, B., Lee, J. H. & Bang, D. Single-cell RNA sequencing technologies and bioinformatics pipelines. _Exp. Mol.

Med._ 50, 1–14 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Satija, R., Farrell, J. A., Gennert, D., Schier, A. F. & Regev, A. Spatial reconstruction of single-cell

gene expression data. _Nat. Biotechnol._ 33, 495–502 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wolf, F. A., Angerer, P. & Theis, F. J. SCANPY: large-scale

single-cell gene expression data analysis. _Genome Biol._ 19, 15 (2018). Article  PubMed  PubMed Central  Google Scholar  * Amezquita, R. A. et al. Orchestrating single-cell analysis with

Bioconductor. _Nat. Methods_ 17, 137–145 (2020). Article  CAS  PubMed  Google Scholar  * Jolliffe, I. T. & Cadima, J. Principal component analysis: a review and recent developments.

_Philos. Trans. A Math. Phys. Eng. Sci._ 374, 20150202 (2016). PubMed  PubMed Central  Google Scholar  * Van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. _J. Mach. Learn.

Res._ 9, 2579−2605 (2008). * McInnes, L., Healy, J. & Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. _arXiv_ https://arxiv.org/abs/1802.03426

(2018). * Traag, V. A., Waltman, L. & Van Eck, N. J. From Louvain to Leiden: guaranteeing well-connected communities. _Sci. Rep._ 9, 5233 (2019). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Ester, M., Kriegel, H.-P., Sander, J. & Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. _In Kdd_ 96, 226–231 (1996).

Google Scholar  * Guo, M., Wang, H., Potter, S. S., Whitsett, J. A. & Xu, Y. SINCERA: a pipeline for single-cell RNA-seq profiling analysis. _PLoS Comput. Biol._ 11, e1004575 (2015).

Article  PubMed  PubMed Central  Google Scholar  * Trapnell, C. et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. _Nat.

Biotechnol._ 32, 381–386 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * La Manno, G. et al. RNA velocity of single cells. _Nature_ 560, 494–498 (2018). Article  PubMed 

PubMed Central  Google Scholar  * Gayoso, A. et al. Deep generative modeling of transcriptional dynamics for RNA velocity analysis in single cells. _Nat. Methods_ 21, 50–59 (2024). Article 

CAS  PubMed  Google Scholar  * Street, K. et al. Slingshot: cell lineage and pseudotime inference for single-cell transcriptomics. _BMC Genomics_ 19, 1–16 (2018). Article  Google Scholar  *

Wolf, F. A. et al. PAGA: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. _Genome Biol._ 20, 9 (2019). Article  Google

Scholar  * Herman, J. S., Sagar, N. & Gruen, D. FateID infers cell fate bias in multipotent progenitors from single-cell RNA-seq data. _Nat. Methods_ 15, 379–386 (2018). Article  CAS 

PubMed  Google Scholar  * Badia, I. M. P. et al. Gene regulatory network inference in the era of single-cell multi-omics. _Nat. Rev. Genet._ 24, 739–754 (2023). Article  Google Scholar  *

Qiu, X. et al. Inferring causal gene regulatory networks from coupled single-cell expression dynamics using scribe. _Cell Syst._ 10, 265–274. e211 (2020). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Greenfield, A., Madar, A., Ostrer, H. & Bonneau, R. DREAM4: combining genetic and dynamic information to identify biological networks and dynamical models.

_PLoS One_ 5, e13397 (2010). Article  PubMed  PubMed Central  Google Scholar  * Huynh-Thu, V. A., Irrthum, A., Wehenkel, L. & Geurts, P. Inferring regulatory networks from expression

data using tree-based methods. _PLoS One_ 5, e12776 (2010). Article  PubMed  PubMed Central  Google Scholar  * Moerman, T. et al. GRNBoost2 and Arboreto: efficient and scalable inference of

gene regulatory networks. _Bioinformatics_ 35, 2159–2161 (2019). Article  CAS  PubMed  Google Scholar  * Chan, T. E., Stumpf, M. P. H. & Babtie, A. C. Gene regulatory network inference

from single-cell data using multivariate information measures. _Cell Syst._ 5, 251–267.e253 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Specht, A. T. & Li, J. LEAP:

constructing gene co-expression networks for single-cell RNA-sequencing data using pseudotime ordering. _Bioinformatics_ 33, 764–766 (2017). Article  CAS  PubMed  Google Scholar  * Aibar, S.

et al. SCENIC: single-cell regulatory network inference and clustering. _Nat. Methods_ 14, 1083–1086 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Bravo Gonzalez-Blas, C.

et al. SCENIC+: single-cell multiomic inference of enhancers and gene regulatory networks. _Nat. Methods_ 20, 1355–1367 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Fleck,

J. S. et al. Inferring and perturbing cell fate regulomes in human brain organoids. _Nature_ 621, 365–372 (2023). Article  CAS  PubMed  Google Scholar  * Wang, L. et al. Dictys: dynamic

gene regulatory network dissects developmental continuum with single-cell multiomics. _Nat. Methods_ 20, 1368–1378 (2023). Article  CAS  PubMed  Google Scholar  * Kamimoto, K. et al.

Dissecting cell identity via network inference and in silico gene perturbation. _Nature_ 614, 742–751 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Lim, C. Y. et al. BTR:

training asynchronous Boolean models using single-cell expression data. _BMC Bioinformatics_ 17, 355 (2016). Article  PubMed  PubMed Central  Google Scholar  * Woodhouse, S., Piterman, N.,

Wintersteiger, C. M., Gottgens, B. & Fisher, J. SCNS: a graphical tool for reconstructing executable regulatory networks from single-cell genomic data. _BMC Syst. Biol._ 12, 59 (2018).

Article  PubMed  PubMed Central  Google Scholar  * Luo, S., Wang, Z., Zhang, Z., Zhou, T. & Zhang, J. Genome-wide inference reveals that feedback regulations constrain promoter-dependent

transcriptional burst kinetics. _Nucleic Acids Res._ 51, 68–83 (2023). Article  CAS  PubMed  Google Scholar  * Matsumoto, H. et al. SCODE: an efficient regulatory network inference

algorithm from single-cell RNA-Seq during differentiation. _Bioinformatics_ 33, 2314–2321 (2017). Article  PubMed  PubMed Central  Google Scholar  * Matsumoto, H. & Kiryu, H. SCOUP: a

probabilistic model based on the Ornstein-Uhlenbeck process to analyze single-cell expression data during differentiation. _BMC Bioinformatics_ 17, 232 (2016). Article  PubMed  PubMed

Central  Google Scholar  * Osorio, D. et al. scTenifoldKnk: an efficient virtual knockout tool for gene function predictions via single-cell gene regulatory network perturbation. _Patterns_

3, 100434 (2022). * Black, H. S. Stabilized feedback amplifiers. _Bell Syst. Tech. J._ 13, 1–18 (1934). Article  Google Scholar  * Wolkenhauer, O., Kitano, H. & Kwang-Hyun, C. Systems

biology. _IEEE Control Syst. Mag._ 23, 38–48 (2003). Article  Google Scholar  * Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. _nature_ 473, 167–173

(2011). Article  CAS  PubMed  Google Scholar  * Valente, T. W., Coronges, K., Lakon, C. & Costenbader, E. How correlated are network centrality measures? _Connect (Tor.)_ 28, 16–26

(2008). PubMed  Google Scholar  * Liu, Y. Y., Slotine, J. J. & Barabasi, A. L. Control centrality and hierarchical structure in complex networks. _PLoS One_ 7, e44459 (2012). Article 

CAS  PubMed  PubMed Central  Google Scholar  * Yang, G., Gomez Tejeda Zanudo, J. & Albert, R. Target control in logical models using the domain of influence of nodes. _Front. Physiol._

9, 454 (2018). Article  PubMed  PubMed Central  Google Scholar  * Mochizuki, A., Fiedler, B., Kurosawa, G. & Saito, D. Dynamics and control at feedback vertex sets. II: a faithful

monitor to determine the diversity of molecular activities in regulatory networks. _J. Theor. Biol._ 335, 130–146 (2013). Article  PubMed  Google Scholar  * Zanudo, J. G. & Albert, R.

Cell fate reprogramming by control of intracellular network dynamics. _PLoS Comput. Biol._ 11, e1004193 (2015). Article  PubMed  PubMed Central  Google Scholar  * Crespo, I., Perumal, T. M.,

Jurkowski, W. & del Sol, A. Detecting cellular reprogramming determinants by differential stability analysis of gene regulatory networks. _BMC Syst. Biol._ 7, 140 (2013). Article 

PubMed  PubMed Central  Google Scholar  * Yang, J.-M., Lee, C.-K. & Cho, K.-H. Robust stabilizing control of perturbed biological networks via coordinate transformation and algebraic

analysis. _In:_ IEEE Transactions on Neural Networks and Learning Systems (2022). * Steinway, S. N. et al. Network modeling of TGFbeta signaling in hepatocellular carcinoma

epithelial-to-mesenchymal transition reveals joint sonic hedgehog and Wnt pathway activation. _Cancer Res._ 74, 5963–5977 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Choi, S. R., Hwang, C. Y., Lee, J. & Cho, K. H. Network analysis identifies regulators of basal-like breast cancer reprogramming and endocrine therapy vulnerability. _Cancer Res._ 82,

320–333 (2022). Article  CAS  PubMed  Google Scholar  * Kim, N., Hwang, C. Y., Kim, T., Kim, H. & Cho, K. H. A cell-fate reprogramming strategy reverses epithelial-to-mesenchymal

transition of lung cancer cells while avoiding hybrid states. _Cancer Res._ 83, 956–970 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * An, S. et al. Inhibition of

3-phosphoinositide-dependent protein kinase 1 (PDK1) can revert cellular senescence in human dermal fibroblasts. _Proc. Natl Acad. Sci. USA_ 117, 31535–31546 (2020). Article  CAS  PubMed 

PubMed Central  Google Scholar  * Seo, C. H., Kim, J. R., Kim, M. S. & Cho, K. H. Hub genes with positive feedbacks function as master switches in developmental gene regulatory networks.

_Bioinformatics_ 25, 1898–1904 (2009). Article  CAS  PubMed  Google Scholar  * Kumar, L. et al. Molecular mechanisms and applications of N-acyl homoserine lactone-mediated quorum sensing in

bacteria. _Molecules_ 27, https://doi.org/10.3390/molecules27217584 (2022). * Chickarmane, V., Troein, C., Nuber, U. A., Sauro, H. M. & Peterson, C. Transcriptional dynamics of the

embryonic stem cell switch. _PLoS Comput. Biol._ 2, e123 (2006). Article  PubMed  PubMed Central  Google Scholar  * Xu, J. & Orkin, S. H. The erythroid/myeloid lineage fate paradigm

takes a new player. _Embo J._ 30, 983–985 (2011). Article  CAS  PubMed  PubMed Central  Google Scholar  * Lu, M., Jolly, M. K., Levine, H., Onuchic, J. N. & Ben-Jacob, E. MicroRNA-based

regulation of epithelial-hybrid-mesenchymal fate determination. _Proc. Natl Acad. Sci. USA_ 110, 18144–18149 (2013). Article  CAS  PubMed  PubMed Central  Google Scholar  * Hornung, G. &

Barkai, N. Noise propagation and signaling sensitivity in biological networks: a role for positive feedback. _PLoS Comput. Biol._ 4, e8 (2008). Article  PubMed  PubMed Central  Google

Scholar  * Kim, J. R. et al. Reduction of complex signaling networks to a representative kernel. _Sci. Signal_ 4, ra35 (2011). Article  PubMed  Google Scholar  * Kim, J., Park, S. M. &

Cho, K. H. Discovery of a kernel for controlling biomolecular regulatory networks. _Sci. Rep._ 3, 2223 (2013). Article  PubMed  PubMed Central  Google Scholar  * An, S. et al. Global

stabilizing control of large-scale biomolecular regulatory networks. _Bioinformatics_ 39, btad045 (2023). * Kwon, Y. K. & Cho, K. H. Boolean dynamics of biological networks with multiple

coupled feedback loops. _Biophys. J._ 92, 2975–2981 (2007). Article  CAS  PubMed  PubMed Central  Google Scholar  * Deritei, D., Rozum, J., Ravasz Regan, E. & Albert, R. A feedback loop

of conditionally stable circuits drives the cell cycle from checkpoint to checkpoint. _Sci. Rep._ 9, 16430 (2019). Article  PubMed  PubMed Central  Google Scholar  * Hu, Y. et al. Optimal

control nodes in disease-perturbed networks as targets for combination therapy. _Nat. Commun._ 10, 2180 (2019). Article  PubMed  PubMed Central  Google Scholar  * Rukhlenko, O. S. et al.

Control of cell state transitions. _Nature_ 609, 975–985 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  * Torborg, S. R., Li, Z. X., Chan, J. E. & Tammela, T. Cellular and

molecular mechanisms of plasticity in cancer. _Trends Cancer_ 8, 735–746 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  * Barkley, D., Rao, A., Pour, M., Franca, G. S. &

Yanai, I. Cancer cell states and emergent properties of the dynamic tumor system. _Genome Res._ 31, 1719–1727 (2021). Article  PubMed  PubMed Central  Google Scholar  * Hanahan, D. Hallmarks

of cancer: new dimensions. _Cancer Discov._ 12, 31–46 (2022). Article  CAS  PubMed  Google Scholar  * Marjanovic, N. D. et al. Emergence of a high-plasticity cell state during lung cancer

evolution. _Cancer Cell_ 38, 229–246.e213 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Zhu, J., Chu, P. & Fu, X. Unbalanced response to growth variations reshapes the

cell fate decision landscape. _Nat. Chem. Biol._ 19, 1097–1104 (2023). Article  CAS  PubMed  Google Scholar  * Papili Gao, N., Ud-Dean, S. M. M., Gandrillon, O. & Gunawan, R.

SINCERITIES: inferring gene regulatory networks from time-stamped single cell transcriptional expression profiles. _Bioinformatics_ 34, 258–266 (2018). Article  PubMed  Google Scholar  *

Zhang, S. et al. Inference of cell type-specific gene regulatory networks on cell lineages from single cell omic datasets. _Nat. Commun._ 14, 3064 (2023). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Kartha, V. K. et al. Functional inference of gene regulation using single-cell multi-omics. _Cell Genom_ 2, 100166 (2022). Download references ACKNOWLEDGEMENTS The

authors thank Corbin Hopper for his critical reading and comments. This work was supported by the National Research Foundation of Korea (NRF) grants funded by the Korean government, the

Ministry of Science and ICT (2023R1A2C3002619 and 2021M3A9I4024447 (Bio & Medical Technology Development Program)). AUTHOR INFORMATION Author notes * Namhee Kim Present address:

biorevert, Inc., Daejeon, Republic of Korea * These authors contributed equally: Jonghoon Lee, Namhee Kim. AUTHORS AND AFFILIATIONS * Laboratory for Systems Biology and Bio-inspired

Engineering, Department of Bio and Brain Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, 34141, Republic of Korea Jonghoon Lee, Namhee Kim & Kwang-Hyun

Cho Authors * Jonghoon Lee View author publications You can also search for this author inPubMed Google Scholar * Namhee Kim View author publications You can also search for this author

inPubMed Google Scholar * Kwang-Hyun Cho View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS All authors contributed to the discussion of the

content, writing, reviewing, and editing the manuscript. K.-H.C. conceived the idea, designed the project, and supervised the study. CORRESPONDING AUTHOR Correspondence to Kwang-Hyun Cho.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which

permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to

the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Lee, J., Kim, N. & Cho, KH. Decoding the principle of cell-fate determination for its reverse control. _npj Syst Biol Appl_ 10, 47

(2024). https://doi.org/10.1038/s41540-024-00372-2 Download citation * Received: 11 December 2023 * Accepted: 16 April 2024 * Published: 06 May 2024 * DOI:

https://doi.org/10.1038/s41540-024-00372-2 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative