News Reader.info

ABSTRACT Hybrid quantum materials allow for quantum phases that otherwise do not exist in nature1,2. For example, a one-dimensional topological superconductor with Majorana states bound to

its ends can be realized by coupling a semiconductor nanowire to a superconductor in the presence of a strong magnetic field3,4,5. However, the applied magnetic fields are detrimental to

superconductivity, and constrain device layout, components, materials, fabrication and operation6. Early on, an alternative source of Zeeman coupling that circumvents these constraints—using

a ferromagnetic insulator instead of an applied field—was proposed theoretically7. Here, we report transport measurements in hybrid nanowires using epitaxial layers of superconducting Al

and the ferromagnetic insulator EuS on semiconducting InAs nanowires. We infer a remanent effective Zeeman field exceeding 1 T and observe stable zero-bias conductance peaks in bias

spectroscopy at zero applied field, consistent with topological superconductivity. Hysteretic spectral features in applied magnetic field support this picture. Access through your

institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your institution Access Nature and 54 other Nature Portfolio

journals Get Nature+, our best-value online-access subscription $32.99 / 30 days cancel any time Learn more Subscribe to this journal Receive 12 print issues and online access $259.00 per

year only $21.58 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated

during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS GIANT

MAGNETOCHIRAL ANISOTROPY FROM QUANTUM-CONFINED SURFACE STATES OF TOPOLOGICAL INSULATOR NANOWIRES Article Open access 12 May 2022 SEMICONDUCTOR-FERROMAGNET-SUPERCONDUCTOR PLANAR

HETEROSTRUCTURES FOR 1D TOPOLOGICAL SUPERCONDUCTIVITY Article Open access 18 August 2022 EPITAXIAL PB ON INAS NANOWIRES FOR QUANTUM DEVICES Article 10 May 2021 DATA AVAILABILITY Source data

are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

REFERENCES * Stern, A. Non-Abelian states of matter. _Nature_ 464, 187–193 (2010). Article  ADS  Google Scholar  * Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana

fermions at the surface of a topological insulator. _Phys. Rev. Lett._ 100, 096407 (2008). Article  ADS  Google Scholar  * Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and

Majorana bound states in quantum wires. _Phys. Rev. Lett._ 105, 177002 (2010). Article  ADS  Google Scholar  * Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a

topological phase transition in semiconductor–superconductor heterostructures. _Phys. Rev. Lett._ 105, 077001 (2010). Article  ADS  Google Scholar  * Lutchyn, R. M. et al. Majorana zero

modes in superconductor–semiconductor heterostructures. _Nat. Rev. Mater._ 3, 52–68 (2018). Article  ADS  Google Scholar  * Karzig, T. et al. Scalable designs for

quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. _Phys. Rev. B_ 95, 235305 (2017). Article  ADS  Google Scholar  * Sau, J. D., Lutchyn, R. M.,

Tewari, S. & Das Sarma, S. Generic new platform for topological quantum computation using semiconductor heterostructures. _Phys. Rev. Lett._ 104, 040502 (2010). Article  ADS  Google

Scholar  * Tedrow, P. M., Tkaczyk, J. E. & Kumar, A. Spin-polarized electron tunneling study of an artificially layered superconductor with internal magnetic field: EuO–Al. _Phys. Rev.

Lett._ 56, 1746–1749 (1986). Article  ADS  Google Scholar  * Meservey, R., Tedrow, P. M. & Fulde, P. Magnetic field splitting of the quasiparticle states in superconducting aluminum

films. _Phys. Rev. Lett._ 25, 1270–1272 (1970). Article  ADS  Google Scholar  * Izyumov, Y. A., Proshin, Y. N. & Khusainov, M. G. Competition between superconductivity and magnetism in

ferromagnet/superconductor heterostructures. _Phys.-Uspekhi_ 45, 109–148 (2007). Article  ADS  Google Scholar  * Bergeret, F. S., Silaev, M., Virtanen, P. & Heikkilä, T. T. Colloquium:

Nonequilibrium effects in superconductors with a spin-splitting field. _Rev. Mod. Phys._ 90, 041001 (2018). Article  ADS  Google Scholar  * Heikkilä, T. T., Silaev, M., Virtanen, P. &

Bergeret, F. S. Thermal, electric and spin transport in superconductor/ferromagnetic–insulator structures. _Prog. Surf. Sci._ 94, 100540 (2019). Article  Google Scholar  * Tokuyasu, T.,

Sauls, J. A. & Rainer, D. Proximity effect of a ferromagnetic insulator in contact with a superconductor. _Phys. Rev. B_ 38, 8823–8833 (1988). Article  ADS  Google Scholar  * Bergeret,

F., Volkov, A. & Efetov, K. Induced ferromagnetism due to superconductivity in superconductor–ferromagnet structures. _Phys. Rev. B_ 69, 174504 (2004). Article  ADS  Google Scholar  *

Strambini, E. et al. Revealing the magnetic proximity effect in EuS/Al bilayers through superconducting tunneling spectroscopy. _Phys. Rev. Mater._ 1, 054402 (2017). Article  Google Scholar

  * Wolf, M., Sürgers, C., Fischer, G. & Beckmann, D. Spin-polarized quasiparticle transport in exchange-split superconducting aluminum on europium sulfide. _Phys. Rev. B_ 90, 144509

(2014). Article  ADS  Google Scholar  * Cottet, A., Huertas-Hernando, D., Belzig, W. & Nazarov, Y. V. Spin-dependent boundary conditions for isotropic superconducting Green’s functions.

_Phys. Rev. B_ 80, 184511 (2009). Article  ADS  Google Scholar  * Liu, Y. et al. Semiconductor–ferromagnetic insulator–superconductor nanowires: stray field and exchange field. _Nano Lett._

20, 456–462 (2020). Article  ADS  Google Scholar  * Desjardins, M. et al. Synthetic spin–orbit interaction for Majorana devices. _Nat. Mater._ 18, 1060–1064 (2019). Article  ADS  Google

Scholar  * Manna, S. et al. Signature of a pair of majorana zero modes in superconducting gold surface states. _Proc. Natl Acad. Sci. USA_ 117, 8775–8782 (2020). Article  Google Scholar  *

Diesch, S. et al. Creation of equal-spin triplet superconductivity at the Al/EuS interface. _Nat. Commun._ 9, 5248 (2018). Article  ADS  Google Scholar  * Liu, Y. et al. Coherent epitaxial

semiconductor–ferromagnetic insulator InAs/EuS interfaces: band alignment and magnetic structure. _ACS Appl. Mater. Interfaces_ 12, 8780–8787 (2020). Article  Google Scholar  * Krogstrup, P.

et al. Epitaxy of semiconductor–superconductor nanowires. _Nat. Mater._ 14, 400–406 (2015). Article  ADS  Google Scholar  * Vaitiekėnas, S., Krogstrup, P. & Marcus, C. Anomalous

metallic phase in tunable destructive superconductors. _Phys. Rev. B_ 101, 060507 (2020). Article  ADS  Google Scholar  * Xiong, Y., Stadler, S., Adams, P. & Catelani, G. Spin-resolved

tunneling studies of the exchange field in EuS/Al bilayers. _Phys. Rev. Lett._ 106, 247001 (2011). Article  ADS  Google Scholar  * Deng, M.-T. et al. Majorana bound state in a coupled

quantum-dot hybrid-nanowire system. _Science_ 354, 1557–1562 (2016). Article  ADS  Google Scholar  * Stanescu, T. D., Lutchyn, R. M. & Das Sarma, S. Majorana fermions in semiconductor

nanowires. _Phys. Rev. B_ 84, 144522 (2011). Article  ADS  Google Scholar  * Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor–semiconductor nanowire devices.

_Science_ 336, 1003–1007 (2012). Article  ADS  Google Scholar  * Nichele, F. et al. Scaling of Majorana zero-bias conductance peaks. _Phys. Rev. Lett._ 119, 136803 (2017). Article  ADS 

Google Scholar  * Vuik, A., Nijholt, B., Akhmerov, A. R. & Wimmer, M. Reproducing topological properties with quasi-Majorana states. _SciPost Phys._ 7, 061 (2019). Article  ADS 

MathSciNet  Google Scholar  * Clarke, D. J. Experimentally accessible topological quality factor for wires with zero energy modes. _Phys. Rev. B_ 96, 201109 (2017). Article  Google Scholar 

* Prada, E., Aguado, R. & San-Jose, P. Measuring Majorana nonlocality and spin structure with a quantum dot. _Phys. Rev. B_ 96, 085418 (2017). Article  ADS  Google Scholar  * Deng, M.-T.

et al. Nonlocality of Majorana modes in hybrid nanowires. _Phys. Rev. B_ 98, 085125 (2018). Article  ADS  Google Scholar  * Bagrets, D. & Altland, A. Class D spectral peak in Majorana

quantum wires. _Phys. Rev. Lett._ 109, 227005 (2012). Article  ADS  Google Scholar  * Nijholt, B. & Akhmerov, A. R. Orbital effect of magnetic field on the Majorana phase diagram. _Phys.

Rev. B_ 93, 235434 (2016). Article  ADS  Google Scholar  * Bruno, R. C. & Schwartz, B. B. Magnetic field splitting of the density of states of thin superconductors. _Phys. Rev. B_ 8,

3161–3178 (1973). Article  ADS  Google Scholar  * Abrikosov, A. A. & Gorkov, L. P. Contribution to the theory of superconducting alloys with paramagnetic impurities. _Sov. Phys. JETP_

12, 1243–1253 (1961). Google Scholar  * Tinkham, M. _Introduction to Superconductivity_ (Dover, 1996). * Bardeen, J. Critical fields and currents in superconductors. _Rev. Mod. Phys._ 34,

667–681 (1962). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS We thank Z. Cui, K. Moler and I. Zhang for EuS magnetization studies, C. Sørensen for contributions to

materials growth, S. Upadhyay for nanofabrication and K. Flensberg for valuable discussions. Research was supported by Microsoft, the Danish National Research Foundation and the European

Commission. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Center for Quantum Devices, Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark S. Vaitiekėnas, Y. Liu, P. Krogstrup

 & C. M. Marcus * Microsoft Quantum Lab—Copenhagen, Copenhagen, Denmark S. Vaitiekėnas & C. M. Marcus * Microsoft Quantum Materials Lab—Copenhagen, Lyngby, Denmark Y. Liu & P.

Krogstrup Authors * S. Vaitiekėnas View author publications You can also search for this author inPubMed Google Scholar * Y. Liu View author publications You can also search for this author

inPubMed Google Scholar * P. Krogstrup View author publications You can also search for this author inPubMed Google Scholar * C. M. Marcus View author publications You can also search for

this author inPubMed Google Scholar CONTRIBUTIONS Y.L. and P.K. developed the nanowire materials. S.V. fabricated the devices, performed measurements and analysed the data with input from

C.M.M. All authors contributed to interpreting the data. The manuscript was written by S.V. and C.M.M. with input from all authors. CORRESPONDING AUTHOR Correspondence to C. M. Marcus.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Physics_ thanks Peng Wei and the other, anonymous,

reviewer(s) for their contribution to the peer review of this work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. EXTENDED DATA EXTENDED DATA FIG. 1 NON-OVERLAPPING AL/EUS SHELL CHARACTERISTICS. A, Four-probe differential resistance of the Al shell adjacent to EuS, _R_S, measured for

device 7 around zero bias as a function of temperature, _T_, shows a critical temperature _T_C0 ~ 1.5 K. Inset: Schematic wire cross section showing orientation of Al and EuS shells on

adjacent pairs of facets. B,C, _R_S as a function of applied magnetic field along wire axis, _H_∥, and current bias, _I_S, sweeping _H_∥ from (B) negative to positive and (C) positive to

negative. Source data EXTENDED DATA FIG. 2 BIAS SPECTROSCOPY OF WIRE WITH NON-OVERLAPPING AL AND EUS SHELLS. A, Colorized micrograph of device 8 with the measurement set-up. External axial

magnetic field, _H_∥, is indicated by an arrow. B, Differential conductance, _G_, as a function of source-drain bias voltage, _V_, at _H_∥ = 0 shows a hard induced superconducting gap around

_Δ_ = 230_μ_eV. Inset: Schematic wire cross section showing orientation of Al and EuS shells on adjacent pairs of facets. C, Evolution of the tunneling spectrum with _H_∥ swept from

negative to positive. D, Difference of two conductance maps taken with _H_∥ swept to opposite directions illustrates a weak hysteresis. The data were taken at _V_C = − 6.65 V, _V_U = − 7 V

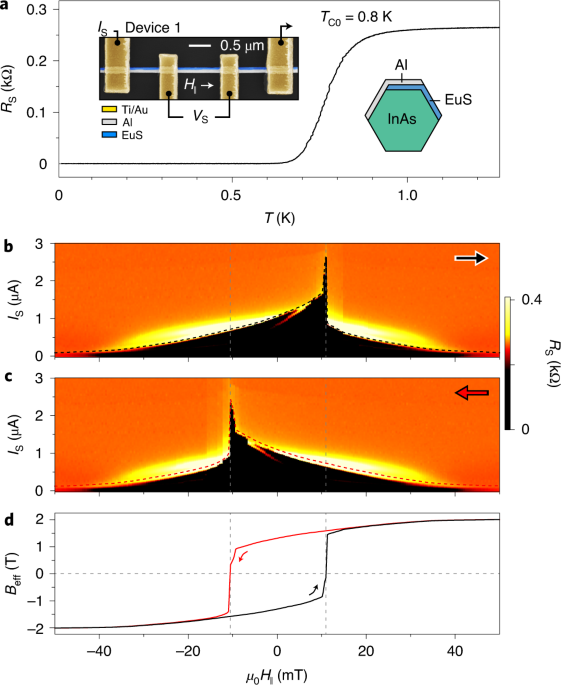
and _V_L = 1.65 V. Source data EXTENDED DATA FIG. 3 CRITICAL TEMPERATURE AND PAIR-BREAKING PARAMETER. A, Critical temperature, _T_C, for device 1 as a function of applied axial magnetic

field, _H_∥, deduced from the critical current fits shown in Fig. 1b,c using Eq. (2). B, Pair-breaking parameter, _α_, estimated using Eq. (1) as described in Methods. Source data EXTENDED

DATA FIG. 4 ZERO-BIAS PEAK SPECTRUM EVOLUTION WITH BARRIER-GATE AND BACK-GATE VOLTAGES. A, Differential conductance, _G_, measured for device 2 at zero bias as a function of barrier-gate

voltage, _V_C, and back-gate voltage, _V_BG. B, Left: _G_ as a function of source-drain bias voltage, _V_, and _V_C measured at _V_BG = − 3.15 V. Right: Line-cut plots of _G_ with subtracted

line resistance, \(\widetilde{G}\), (see Methods) taken from the right panel at various _V_C values. C–H, Similar to B measured within the white box in A at various _V_BG values ranging

from − 3.05 V to − 2.55 V every 0.1 V. All the sweeps display a zero-bias peak that evolves into a zero-bias dip, with the crossover-conductance values varying from 0.2 _e_2/_h_ to above

_e_2/_h_ depending on _V_BG. All the measurements were taken at _V_L = 0 V, _V_U = − 1 V, and zero applied magnetic field _H_∥ = 0. Source data EXTENDED DATA FIG. 5 LINE-CUT PLOTS AT VARIOUS

BARRIER-GATE VOLTAGES. Same data as in Extended Data Fig. 4c,e,g. A, Differential conductance with subtracted line resistance, \(\widetilde{G}\), (see Methods) measured for device 2 as a

function of source-drain bias voltage, _V_, at various barrier-gate voltage _V_C values ranging from − 1.3 V to − 1.0 V every 2 mV and fixed back-gate voltage _V_BG = − 3.05 V. B,C, Same as

(a) but measured at _V_BG = − 2.85 V and _V_BG = − 2.65 V, respectively. Source data EXTENDED DATA FIG. 6 TUNNELING SPECTRUM EVOLUTION WITH UPPER- AND LOWER-GATE VOLTAGES. A–H, Differential

conductance, _G_, measured for device 2 as a function of source-drain voltage bias, _V_, and upper-gate voltage, _V_U, taken at various lower-gate voltage, _V_L, values. A pair of faint

subgap states is visible for _V_L close to zero. As _V_L is reduced, a stable zero-bias peak develops around _V_L = − 0.6 V, but then splits again for more negative voltages. I, _G_

dependence on _V_U taken at _V_L = − 0.65 V while compensating with _V_C to maintain barrier iso-potential. J, Similar to I but as a function of _V_L taken at _V_U = − 0.7 V. The sharp

resonances in I and J are due to charge motion in the junction and do not split the zero-bias peak. K, L, Zoom-ins on the end-state resonances visible in J. All the measurements were taken

at back-gate voltage _V_BG = − 3 V and zero applied magnetic field _H_∥ = 0. Source data EXTENDED DATA FIG. 7 SPECTRUM EVOLUTION WITH DIFFERENT GATE VOLTAGES. A, Differential conductance,

_G_, measured for device 2 as a function of source-drain bias voltage, _V_ and back-gate voltage, _V_BG, measured along white dashed line in Fig. 2b, at _V_L = 0 V and _V_U = − 1 V. B,

Line-cut plots of _G_ with subtracted line resistance, \(\widetilde{G}\), (see Methods) taken from A at various _V_BG values. C,D, Similar to A,B but for device 3 as a function of upper-gate

voltage, _V_U, measured at _V_BG = − 5 V, _V_L = − 0.5 V, and _V_C = − 1.705 V. E,F, Similar to A,B but for device 4 as a function of lower-gate voltage, _V_L, measured at _V_BG = 0.5 V,

_V_U = − 0.8 V, and _V_C = − 0.89 V. All the measurements were taken at zero applied magnetic field _H_∥ = 0. Source data EXTENDED DATA FIG. 8 ROBUST ZERO-BIAS PEAK AT COERCIVE FIELDS. A,

Differential conductance, _G_, as a function of source drain voltage bias, _V_, and applied axial magnetic field, _H_∥, for device 4 at _V_L = − 0.32 V in Fig. 2f, on the less negative gate

voltage side of the zero-bias peak splitting. Sweep direction indicated by arrow. Zero-bias peak is continuous through magnetization reversal. B, Same as A with sweep direction from positive

to negative. The data were taken at _V_BG = 0.5 V, _V_U = − 0.8 V, and _V_C = − 0.89 V. Source data EXTENDED DATA FIG. 9 ADDITIONAL IN-PLANE FIELD ANGLE MEASUREMENTS. A, Differential

conductance, _G_, measured for device 6 [lithographically equivalent to device 2 shown in Fig. 2a but with wire length of 1 _μ_m] as a function of source-drain bias voltage, _V_ and

lower-gate voltage, _V_L. Top axis shows compensation gate voltages. The data were taken at _V_BG = − 1 V, _V_U = 0 V, and zero applied magnetic field _H_∥ = 0. B, _G_ dependence on in-plane

angle, _φ_ [see Fig. 2a for orientation], taken at a fix external magnetic field amplitude, _μ_0_H__φ_ = 30 mT and a gate configuration corresponding to _V_L = − 0.9 V in A shows a

zero-bias peak robust for all _φ_. Source data EXTENDED DATA FIG. 10 COERCIVE FIELD DEPENDENCE ON IN-PLANE FIELD ANGLE. A, Difference of two conductance maps measured for device 2 with axial

magnetic field, _H_∥, swept to opposite directions, as a function of source-drain bias voltage, _V_, showing coercive field _H_∥,C = ± 49 mT. B–E, Similar to A but with field, _H__φ_, swept

at in-plane angle, _φ_ [see Fig. 2a for orientation]. The amplitude of coercive field, _H__φ_,C, increases with _φ_. See Supplementary Information for the corresponding conductance maps. F,

_H__φ_,C measured from A-E as a function of _φ_ increases as \(1/\cos (\varphi )\). G, Same data as in F multiplied by \(\cos (\varphi )\) does not depend on _φ_, indicating that the EuS

magnetization is along the wire axis and that only the _H_∥ component controls magnetization. All the measurements were taken at _V_BG = − 3 V, _V_L = − 0.65 V, _V_U = − 0.6 V, and _V_C = −

1.1875 V. Source data SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Figs. 1–4. SUPPLEMENTARY DATA 1 Supplementary Data 1. SUPPLEMENTARY DATA 2 Supplementary Data 2.

SUPPLEMENTARY DATA 3 Supplementary Data 3. SUPPLEMENTARY DATA 4 Supplementary Data 4. SOURCE DATA SOURCE DATA FIG. 1 Source Data for Fig. 1. SOURCE DATA FIG. 2 Source Data for Fig. 2. SOURCE

DATA FIG. 3 Source Data for Fig. 3. SOURCE DATA FIG. 4 Source Data for Fig. 4. SOURCE DATA EXTENDED DATA FIG. 1 Source Data for Extended Data Fig. 1. SOURCE DATA EXTENDED DATA FIG. 2 Source

Data for Extended Data Fig. 2. SOURCE DATA EXTENDED DATA FIG. 3 Source Data for Extended Data Fig. 3. SOURCE DATA EXTENDED DATA FIG. 4 Source Data for Extended Data Fig. 4. SOURCE DATA

EXTENDED DATA FIG. 5 Source Data for Extended Data Fig. 5. SOURCE DATA EXTENDED DATA FIG. 6 Source Data for Extended Data Fig. 6. SOURCE DATA EXTENDED DATA FIG. 7 Source Data for Extended

Data Fig. 7. SOURCE DATA EXTENDED DATA FIG. 8 Source Data for Extended Data Fig. 8. SOURCE DATA EXTENDED DATA FIG. 9 Source Data for Extended Data Fig. 9. SOURCE DATA EXTENDED DATA FIG. 10

Source Data for Extended Data Fig. 10. RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Vaitiekėnas, S., Liu, Y., Krogstrup, P. _et al._ Zero-bias peaks

at zero magnetic field in ferromagnetic hybrid nanowires. _Nat. Phys._ 17, 43–47 (2021). https://doi.org/10.1038/s41567-020-1017-3 Download citation * Received: 10 March 2020 * Accepted: 21

July 2020 * Published: 07 September 2020 * Issue Date: January 2021 * DOI: https://doi.org/10.1038/s41567-020-1017-3 SHARE THIS ARTICLE Anyone you share the following link with will be able

to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative