News Reader.info

ABSTRACT While studying the scientific and engineering aspects of a field-portable 3He/4He ratio detector, we found elevated ratios at comparatively lower temperatures that appear to result

from differential diffusion of these isotopes in pure quartz glass. The 3He enrichment relative to 4He in lab air, expressed as the ratio R and normalized to the accepted 3He/4He ratio of

1.40 E-06 (Ra), ranges from peak values of about 200 to 600 in dry static samples. Even at the maximum classical 3He/4He diffusivity ratio of 1.15, the expected R would be only 1.61 E-06.

Within a narrow temperature window, the air value in our experimental set up with pure quartz glass can range from about 2.70 to 8.20 E-04, or nearly 1000 times the expected enrichment based

upon classical fractionation. When plotted versus temperature, the narrow 3He net partial pressure peak reveals at least three sharper embedded peaks that may be quantized vibrational

entrance states in quartz glass which are temperature specific. This discovery has implications for relatively low-energy industrial enrichment of scarce 3He from natural sources on Earth,

and for radiogenic and cosmogenic helium dating assumptions in natural glasses. It also has bearing upon designs for field portable 3He/4He ratio detectors aimed at earthquake and volcanic

eruption studies, and monitoring of nuclear sites. SIMILAR CONTENT BEING VIEWED BY OTHERS HADEAN ISOTOPIC FRACTIONATION OF XENON RETAINED IN DEEP SILICATES Article 22 June 2022 ELECTRICAL

CONDUCTIVITY OF WARM DENSE SILICA FROM DOUBLE-SHOCK EXPERIMENTS Article Open access 05 February 2021 86KR EXCESS AND OTHER NOBLE GASES IDENTIFY A BILLION-YEAR-OLD RADIOGENICALLY-ENRICHED

GROUNDWATER SYSTEM Article Open access 30 June 2022 INTRODUCTION Helium is known to diffuse through glass as a function of temperature, pressure, and purity of the silica glass matrix1,2,3.

The fractionation of the 3He isotope of helium in glass relative to its heavier and far more abundant isotope, 4He, is less well understood. Trull4 studied the fractionation of these

isotopes during diffusion in natural glasses and silicate minerals and found that the enrichment of 3He, expressed as the diffusivity isotope ratio D 3He/D 4He was only 1.08 and not

compositionally dependent, whereas classical mechanics predicts as much as 1.15 based upon their mass ratio. Earlier work by Shelby5 found that the diffusivity isotope ratio for this pair in

vitreous silica was as high as 1.12 at temperatures approaching 600 °C, and ascribed the effect to a quantum correction first proposed by LeClaire6. Here we report experimental data that

indicates the temperature and time-dependent diffusivity ratio, D 3He/D 4He can be far greater than 1.15 in pure quartz glass at temperatures below 300 °C. Quantum tunneling (e.g. ref.7)

over short distances aided by interstice channels is the most plausible mechanism to explain these large 3He enrichments at comparatively low temperature. RESULTS Experiments were conducted

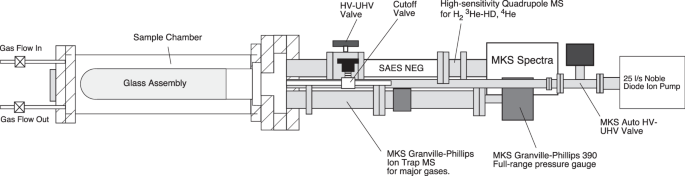
on a compact, elongate vacuum apparatus described in the Methods (Fig. 1). The results presented herein were recorded throughout a typical heating cycle, e.g., from ambient lab temperature

to a maximum temperature usually reached before one hour of applied power and then cooled to near ambient temperature. The trends of a typical, repeatable static lab air heat ramp are shown

in Fig. 2. Two portions of this ramp are highlighted: one (blue) showing enrichments of 3He, HD and H2 and a second portion (purple) showing continued gains in HD and H2 partial pressure

(PP) as the maximum temperature peaks and begins to slowly decrease at the same or slightly higher power level applied to the heating element, i.e., as the glass cools. Heating power was

turned off at the end of these portions. In contrast to the 3He, HD and H2 trends, 4He rises linearly and peaks shortly after heater power ceases. Expressed as the 3He/4He ratio, upon

heating a maximum of 8.20 E-04 is seen at a temperature of 263 °C, the peak ranging from ca. 130° to 370 °C (Fig. 2). Such high ratios exceed those of interplanetary dust particles or the

Moon’s regolith8,9. As we demonstrate below, this enrichment results from differential diffusion of 3He and 4He in heated quartz glass. Some diffusion of these gases may also occur in the

lower-temperature glasses used to fuse the quartz glass to metal, such as Pyrex™ and Kovar™, but these glasses contain metals that block the open Si-O ring structure in pure silica glass,

leading to much lower diffusion rates (c.f. ref.3). Figure 3 presents temporal trend plots of temperature, 4He partial pressure, and Rc/Ra (rationale for this ratio terminology given in

caption) for the case of static flow at six progressively higher power settings. In all cases, heating power was applied for one hour and data recorded until the sample chamber cooled to

about 10 °C above ambient, which ranged from 23° to 25 °C. Net isotope integrals represent the integrated peak response above their respective background levels. Yellow shaded areas

represent the integrated, corrected 4He partial pressure for 200 minutes (arbitrarily set by the V = 110 run). The 3He/4He ratio in blue is the corresponding value for 200-minute

integrations. Between applied AC power levels of 28 to 100 W, 3He net partial pressure builds in the vacuum by diffusion through the glass within the first ca. 20–30 minutes of the heat

ramp, as shown by the Rc/Ra trend. High Rc/Ra values are indicated at 3He peak diffusion temperatures. 4He net partial pressure takes considerably longer to build in the instrument vacuum,

increasing with power level and maximum temperature (Fig. 3). The air ratio is achieved in about 200 minutes at V = 130, but takes over 300 minutes at V = 75. Other power settings show

intermediate and longer-period results; at V = 25, very little 3He relative to 4He is diffusing through the glass. At higher power settings, above V = 50, the 4He conductance increases with

increased maximum glass temperatures as the run progresses. The result is that by the end of the run, the 4He partial pressure overcomes the low-temperature 3He conductance advantage due to

the much greater abundance of 4He. The increased abundance of 4He then raises the noise floor of the quadrupole to above the 3He signal (see panel V = 130, Fig. 3). Except for the two lowest

power ramps, heat ramps were run progressively, with ≥1-hour exposure to the ion pump to reduce the prior sample’s vacuum pressure, usually by greater than an order of magnitude. Subsequent

heat ramps with the sample chamber under vacuum and with dry tank N2 as a pressure compensation have shown a reservoir effect for helium isotopes in glass, which can be cleared after 1–2 

hours of heating to >400 °C (e.g. ref.10). This effect may have added 3He and 4He to the progressive heat ramps in Fig. 3, but does not change the overall results presented. DISCUSSION

AND CONCLUSIONS The 3He enrichment relative to 4He in lab air, expressed as the ratio R and normalized to the accepted 3He/4He ratio of 1.40 E-06 (Ra), ranges from peak values of about 200

to 600 in dry static samples (Figs. 2 and 3). Even at the maximum classical 3He/4He diffusivity ratio of 1.15, the expected R would be only 1.61 E-06. Within a narrow temperature window, the

air value in our experimental set up with pure quartz glass can range from about 2.70 to 8.20 E-04, or nearly 1000 times the expected enrichment based upon classical fractionation. These

enormous enrichment values, and their unexpected variance with temperature are, however, consistent with a quantum tunneling (QT)-enhanced fractionation of 3He/4He in similar molecular

ring-structure matrices (e.g., refs.11,12,13,14,15). However, as indicated in Fig. 3, integration over the duration of the experimental heat ramp produces 3He/4He ratios that closely

approach the accepted value for air. Additional supporting data to the trends presented in Figs. 2 and 3 are presented in the supplementary information section. The tunneling diffusion that

creates the very high 3He/4He fractionation observed in modified graphene is essentially a surface phenomenon involving a few atomic layers and cooled to very low temperatures, but occurs up

to room temperature11,12,13,14,15. It is similar to the resonant tunneling of electrons over distances of about 100 atomic layers in doped semiconductors that allow fast switching in

tunneling diodes (e.g. ref.16). The exact mechanism of resonant tunneling-assisted diffusion in quartz glass up to 2 mm in thickness, as in this study, is presently unknown, but the vitreous

silica contains migration paths for atoms to pass from interstice to interstice through channels formed by Si-O rings10. Indirect evidence for such structural interstices housing helium is

the need for glass heating to high temperature under pressurized nitrogen gas to effectively clear the glass volume of prior helium loads in our experiments. The diffusion mechanism may be

similar to that proposed for hydrogen atom diffusion through amorphous and polycrystalline ice, where tunneling diffusion may occur for a short distance within each single crystal or domain,

whereas it should be highly suppressed for long-distance diffusion beyond steps and grain boundaries17. When plotted versus temperature, the narrow 3He net partial pressure peak reveals at

least three sharper embedded peaks (Fig. 4), corresponding to mean temperatures of 248 °C, 314 °C, and 348 °C within the six heat ramps shown in Fig. 3. These three sharper peaks are

temperature specific and likely responsible for most of the differential diffusion effects observed. Because glass has high thermal insulation properties, the actual temperatures at which

selective 3He transmission phenomena occur are believed to be lower than recorded data. The increased temperatures observed with higher constant power settings (higher voltages) which result

in steeper slopes of temperature rise demonstrate aggravation of this thermal lag effect. These peaks are interpreted as multiple resonant tunneling temperature states in quartz glass for

quantum diffusion of 3He (c.f., refs.16,18). Higher sampling rates should improve the resolution of these temperature peaks, which we anticipate to be very narrow, and in the range of 140°

to 300 °C. 3He shares chemical assignation to 4He but during diffusion through glass it resembles the better-studied quantum tunneling of hydrogen through solids (e.g. ref.17) rather than

the much slower diffusion of 4He. Previous investigations established that the diffusion of helium and its isotopes increases with increasing temperature in both natural and synthetic

silicate glasses4,19,20. These investigations also suggested that there is an increasing fractionation of 3He to 4He with temperature, which is opposite in both sign and magnitude with our

experimental findings in pure quartz glass. Craig and Lupton21 and Rison and Craig22 noted the loss of magmatic helium and large changes in the 3He/4He ratios of natural glasses relative to

vesicles in young submarine basalts (with some alkalic basalts containing thin glass vesicle walls of a mm or less thickness) that they ascribed to low-temperature (ca. 2°–4 °C) exchange

with seawater. These changes may have at least been aided by the extreme fractionation we have found due to QT effects in pure quartz glass. When using the 3He/4He ratios of natural glasses

as a dating tool21,23, the assumption of closed system behavior may have yet another complication to address. The QT effects we have found in pure quartz glass were an inadvertent discovery

made while studying the scientific and engineering aspects of a field-portable 3He/4He ratio detector, on a pathway toward continuous monitoring of these ratios in both natural gases and

fluids that would be useful to the study and prediction of large earthquakes and volcanic eruptions (e.g.24,25,26,27,28). 3He and 4He-based detectors are also useful for monitoring nuclear

storage sites and facilities, both as an intrinsic detector and as a detection medium for neutrons (e.g. ref.29). The trapping efficiency for 3He and 4He in these experiments can be

estimated from their known concentration in dry air, sample volume, average net 3He and 4He PP (from Fig. 3 heat ramps), and volume of the instrument’s vacuum. These calculated efficiencies

are 0.672 and 0.638%, respectively. The 3He/4He diffusion efficiency ratio in quartz glass is, on average, 6.72 E-03/6.38 E-03 = 1.05 ± 0.40. Both isotopes have essentially the same

efficiency despite their disparate relative concentrations in air and temperature dependence. This ratio is similar to the diffusivity ratio reported for natural glasses by Trull4. It is

important to note that the calculations assume that the integration times over the temperature history account for these differential diffusion effects in quartz glass, and similar

integrations may explain why these differential diffusion effects were not previously recognized. Efficiency calculations are shown below. Molar 3He concentration in air sample = n = PV/RT =

 (1 atm) Ra * [4He] * sample volume = (1 atm) 1.40 E-06 (5.22 ppm) (3.28 L) = 1.40 E-06 (5.22 E-06) (3.28 L) = 7.31 E-12 (3.28 L) = 2.40 E-11/[0.08206 (298)] = 9.81 E-13 moles. Molar 3He

concentration in inst. vacuum = n = PV/RT = (0.97 ± 0.34 E-12 Torr [Average and standard error of net integrations for four highest power heat ramps in Fig. 3.]) (1 atm/7.60 E + 02 Torr)

(40.5 C.F. [C.F. = conversion factor calculated between the NIST-traceable ART mass spectrometer-390-gauge PP and those recorded by the MKS Spectra mass spectrometer. Conversion factors were

calculated from highly linear regression slopes of PPs for in-common H2 and 4He, and extrapolated for 3He at intermediate mass/charge.]) (3.12 L)/RT = 6.60 E-15 moles. Absolute 3He

diffusion efficiency = 6.60 E-15 moles/9.81 E-13 moles = 6.72 E-03 or 0.672%. For 4He, these calculations are: Molar 4He concentration in air sample = n = PV/RT = (1 atm) [4He] * sample

volume = (1 atm) (5.22 ppm) (3.28 L)/[0.08206 (298)] = 5.22 E-06 (3.28 L)/24.45 = 7.00 E-07 moles. Molar 4He concentration in inst. vacuum = n = PV/RT = (5.91 ± 2.23 E-07 Torr [Average and

standard error of net integrations for four highest power heat ramps in Fig. 3.]) (1 atm/7.60 E + 02 Torr)(45 C.F. [C.F. = conversion factor calculated between the NIST-traceable ART mass

spectrometer-390-gauge PP and those recorded by the MKS Spectra mass spectrometer. Conversion factors were calculated from highly linear regression slopes of PPs for in-common H2 and 4He,

and extrapolated for 3He at intermediate mass/charge.]) (3.12 L)/RT = (7.78 E-10 atm) (45 C.F.) (3.12 L)/[0.08206 (298)] = 1.09 E-07/24.45 = 4.46 E-09 moles. Absolute 4He diffusion

efficiency = 4.46 E-09 moles/7.00 E-07 moles = 6.38 E-03 or 0.638%. We conclude that the heat ramps performed with this prototype were not highly efficient at transferring He isotopes from

dry air into the instrument’s vacuum. Nevertheless, these experiments demonstrate an effective measurement of the isotope ratio at air concentrations that is temperature dependent, and

suggest that a previously unknown, relatively low-power concentration method may exist for transferring 3He from the atmosphere, heretofore thought too dilute as a potential resource of this

rare isotope. The 3He enrichment window in quartz glass occurs within ca. 150° to 450 °C, with even narrower peaks within this range that are presently poorly resolved but strongly suggest

quantized vibrational entrance temperature states are driving its diffusion via tunneling. Procedural changes such as greater integration time within the temperature window and higher

applied sample pressure, plus design changes such as greater glass surface area and thinner wall thickness would improve the absolute transfer efficiency (c.f. ref.1). The transparency of

the glass transfer medium and the low temperatures required suggest a passive, solar-heated surface array as a concentration facility, requiring little effort except for occasional sweeps of

the vacuum chamber to tantalum getters. METHODS Experiments were made on a compact, elongate vacuum apparatus that featured two vacuums, a high to UHV vacuum chamber and a sample chamber

surrounding a glass inlet that could be evacuated (Fig. 1). We used a cylindrical, “domed” quartz glass adapter assembly sited within a sample chamber where air was introduced via a gas

inlet valve and maintained at constant pressure by pumping or thermally pressurized by valve isolation upon heating. Gases diffuse through the glass and pass into a static UHV Measurement

System that contains both mass spectrometers, vacuum pumps, and total-pressure measurement device. The entire system is constructed with vacuum components consisting of commercial

Conflat™-type stainless steel (SS) flanges and housed in commercial grade 304-stainless steel components with hydrogen partial pressure minimized by Non-Evaporable Getter (NEG) pumping. We

used a high-purity (99.995% SiO2) GE quartz glass cylinder of 2.5-inch (6.35 cm) diameter by 7 inches (17.78 cm) length that was fused with lower-temperature borosilicate glass and Kovar™ to

a 4.5 inch (11.43 cm) Conflat™ SS vacuum flange. The glass vacuum fitting was 2 mm in wall thickness. The glass surface area available for the experiment was 532 cm2. Heat was applied with

a Samox®-coated high-temperature heat tape with power controlled by a Variac™ variable autotransformer. Temperature was monitored using an Omega thermocouple (TC) probe placed to within a

few mm of the glass surface via an Agilent data logger with data simultaneously fed into the MKS Microvision-2 quadrupole mass spectrometer (QMS) through a custom TC interface. The enclosed,

vacuum-tight SS sample chamber had a 4-pin electrical feed-through and welded inlet and outlet SS tubing for both pumped and static (no flow) gas options. Lab air relative humidity ranged

from 50 to 60%, and was dried by re-circulated flow through an indicating chemical desiccant trap prior to inlet into the sample chamber. A SAES Getters NEG pump and a Gamma Vacuum noble

diode ion pump maintained high to UHV conditions after bringing the system within range with a turbo-roughing pump station. The vacuum quality and other gases of interest, specifically H2

and 4He, were monitored with an MKS ART (Auto-Resonant Ion Trap) MS coupled to a NIST-traceable, full-range vacuum gauge (MKS model 390) running on the same PC computer clock as the QMS. The

ART MS computes absolute partial pressures by a ratiometric technique, combining the relative intensity ratios of a chosen peak response to the total MS response with the total pressure

measured simultaneously. The QMS produced factory-calibrated peak response, which we found was offset from the ART by a linearly-calculable factor used for relating the two MS response

values at in-common masses 2 and 4. The MKS Microvision-2 QMS was modified for this application to work at very high frequency in the mass range 1–6 amu, and was thus optimized for

sensitivity at relatively high mass resolution. Scan samples of laboratory air reported herein were continuously collected as near to complete-cycle heat ramps from ambient laboratory

temperatures to maximum temperatures determined by the voltage setting on the Variac. The heating up-ramps were logarithmic curves (R2 ≥ 0.95) that reached 200 °C in 2.8 minutes at V = 130.

Reaching this temperature would take over 15.6 hours at V = 25. After heating for one hour, cooling curves were exponential after line power was cut off (Figs. 2 and 3). Operation of a

high-vacuum valve that isolated the ion pump rapidly cleared He, Ne and Ar which had accumulated in the high vacuum chamber. Hydrogen was continuously pumped by the NEG, along with any

reactive species such as H2O and CH4. The modified MKS quadrupole MS could not resolve contributions to the mass-3 peak from well-known interfering 3He isobars of HD, 3H (tritium) and H3

(triatomic hydrogen). For these experiments, we assumed the contribution from environmental tritium was negligible and concentrated on resolving the HD plus H3 isobars. HD is 0.01% of

environmental hydrogen on Earth but may suggest a different relative abundance in the vacuum components, as shown in the Supplementary Information section. We used two resolution methods.

The first was statistical linear regression from plots of mass-2 versus mass-3, where the abscissa (x-axis) is the H2 peak response and the ordinate (y-axis) is the combined peak response

from 3He and HD. A positive intercept at zero H2 will be residual 3He, as HD and H2 co-vary with an assumed constant ratio (e.g. ref.30). The second method, called herein Adjusted Ionization

Mass Spectrometry (AIMS) (TIMS of ref.31), works by lowering the ionization potential from the standard 70 eV to less than 30 eV, effectively eliminating any 3He, as helium is not

responsive beneath this ionization threshold. The lower ionization mass-3 response is therefore residual HD and H3 (plus any tritium), to be subtracted from the higher ionization peak with

combined 3He, HD, H3, and 3H response. A co-variance with R2 = 0.79 (n = 44) was found for these two methods as “blind temperature ramps”, where QMS scan measurements were recorded

immediately upon cool-down following 1-hour heat ramp completions. Comparison of lab air 3He/4He ratios determined by these two methods were within a factor of 2 of the accepted air ratio of

1.40 E-06 at ramp maximum temperatures above 300 °C (refs27,28,32; see Supplementary Information). DATA AVAILABILITY The datasets generated during and/or analyzed during the current study

are available from the corresponding author on reasonable request. REFERENCES * Norton, F. J. Helium diffusion through glass. _J. Am. Ceram. Soc._ 36, 90–96 (1953). Article  CAS  Google

Scholar  * Rogers, W. A., Buritz, R. S. & Alpert, D. Diffusion coefficient, solubility, and permeability for helium in glass. _J. Appl. Phys._ 25, 868–875 (1954). Article  ADS  CAS 

Google Scholar  * Altemose, V. O. Helium diffusion through glass. _J. Appl. Phys._ 32, 1309–1316 (1961). Article  ADS  CAS  Google Scholar  * Trull, T. W. Diffusion of helium isotopes in

silicate glasses and minerals: Implications for petrogenesis and geochronology. Ph. D. dissertation, Woods Hole Oceanographic Institution and Mass. Inst. Technology, Woods Hole, MA, 399 pp.

(1989). * Shelby, J. E. Diffusion of helium isotopes in vitreous silica. _Phys. Review B_ 4, 2681–2686 (1971). Article  ADS  Google Scholar  * LeClaire, A. D. Some comments on the mass

effect in diffusion. _Phil. Mag._ 14, 1271–1284 (1966). Article  ADS  CAS  Google Scholar  * Razavy, M. _Quantum Theory of Tunneling_, 2nd ed., World Scientific Publ. Co., Ltd., New Jersey,

767 pp., ISBN 9812564888 (2014). * Nier, A. O. & Schlutter, D. J. He-3/He-4 ratios in interplanetary dust particles. _Meteorit._ 29(511), ISSN 0026–1114 (1994). Google Scholar  * Fa, W.

& Jin, Y.-Q. Quantitative estimation of helium-3 spatial distribution in the lunar regolith layer. _Icarus_ 190, 15–23 (2007). Article  ADS  CAS  Google Scholar  * Boiko, G. G. &

Berezhnoi, G. V. Migration paths of helium in α-quartz and vitreous silica from molecular dynamics data. _Glass Phys. and Chem._ 29, 42–48 (2003). Article  CAS  Google Scholar  * Schrier, J.

Helium separation using porous graphene membranes. _J. Phys. Chem. Lett._ 1, 2284–2287 (2010). Article  CAS  Google Scholar  * Schrier, J. & McClain, J. Thermally-driven isotope

separation across nanoporous graphene. _Chem. Phys. Lett._ 521, 118–124 (2012). Article  ADS  CAS  Google Scholar  * Hauser, A. W. & Schwerdtfeger, P. Nanoporous graphene membranes for

efficient 3He/4He separation. _J. Phys. Chem. Lett._ 3, 209–213 (2011). Article  Google Scholar  * Hauser, A. W., Schrier, J. & Schwerdtfeger, P. Helium tunneling through

nitrogen-functionalized graphene pores: pressure- and temperature-driven approaches to isotope separation. _J. Phys. Chem. C_ 116, 10819–10827 (2012). Article  CAS  Google Scholar  * Mandra,

S., Schrier, J. & Ceotto, M. Helium isotope enrichment by resonant tunneling through nanoporous graphene bilayers. _J. Phys. Chem. A_ 118, 6457–6465 (2014). Article  CAS  Google Scholar

  * Shan, Q. _et al_. Transport-mechanism analysis of the reverse leakage current in GaInN light-emitting diodes. _Appl. Phys. Lett._ 99, 253506 (2011). Article  ADS  Google Scholar  *

Kuwahata, K., Hama, T., Kouchi, A. & Watanabe, N. Signatures of quantum-tunneling diffusion of hydrogen atoms on water ice at 10 K. _Phys. Rev. Lett._ 115, 133201 (2015). Article  ADS 

CAS  Google Scholar  * Parra-Murillo, C. A., Madroñero, J. & Wimberger, S. Quantum diffusion and thermalization at resonant tunneling. _Phys. Rev. A_ 89, 053610 (2014). Article  ADS 

Google Scholar  * Shelby, J. E. & Keeton, S. C. Temperature dependence of gas diffusion in glass. _J. Appl. Phys._ 45, 1458–1460 (1974). Article  ADS  CAS  Google Scholar  * Jambon, A.

& Shelby, J. E. Helium diffusion and solubility in obsidians and basaltic glass in the range 200–300 °C. _Earth Planet. Sci. Lett._ 51, 206–214 (1980). Article  ADS  CAS  Google Scholar

  * Craig, H. & Lupton, J. E. Primordial neon, helium, and hydrogen in oceanic basalts. _Earth Planet. Sci. Lett._ 31, 369–385 (1976). Article  ADS  CAS  Google Scholar  * Rison, W.

& Craig, H. Helium isotopes and mantle volatiles in Loihi Seamount and Hawaiian Island basalts and xenoliths. _Earth Planet. Sci. Lett._ 66, 407–426 (1983). Article  ADS  CAS  Google

Scholar  * Kurz, M. D. & Jenkyns, W. J. The distribution of helium in oceanic basalt glasses. _Earth Planet. Sci. Lett._ 53, 41–54 (1981). Article  ADS  CAS  Google Scholar  * Sano, Y.

_et al_. Ten-year helium anomaly prior to the 2014 Mt Ontake eruption. _Sci. Rep._ 5, 13069, https://doi.org/10.1038/srep13069 (2015). Article  ADS  CAS  PubMed  PubMed Central  Google

Scholar  * Padrón, E., _et al_ Diffusive helium emissions as a precursory sign of volcanic unrest. Geology, 41, 539–542; Data Repository item 2013149, https://doi.org/10.1130/G34027.1

(2013). * Bajo, K. _et al_. Construction of a newly designed small-size mass spectrometer for helium isotope analysis: toward the continuous monitoring of 3He/4He ratios in natural fluids.

_Mass Spectrom._ 1, A0009 (2012). Article  ADS  Google Scholar  * McMurtry, G. M. & Hilton, D. R. Towards field measurements of 3He/4He: a key parameter in volcano monitoring.

Goldschmidt 2014 Abstracts, International Geochemical Society, Sacramento, CA, 1657 (abstract) (2014). * McMurtry, G. M., Hilton, D. R. & Blessing, J. E. Development of a field-portable

helium isotope detector for survey and long-term monitoring. International Geochemical Society, Goldschmidt 2016 meeting, Yokohama, Japan (abstract) (2016). * Crane, T. W. & Baker, M. P.

Neutron detectors, in T. D. Reilly, N. Ensslin and H. A. Smith (eds), _Passive Nondestructive Assay of Nuclear Materials_. U. S. Nuclear Regulatory Commission NUREG/CR-5550, Chapt. 13

(1991). * Farley, K. A. _et al_. _In situ_ radiometric and exposure age dating of the Martian surface, supplementary materials. _Science_, https://doi.org/10.1126/science.1247166 (2013). *

Davies, S., Rees, J. A. & Seymour, D. L. Threshold ionization mass spectrometry (TIMS): a complementary quantitative technique to conventional mass resolved mass spectrometry. _Vacuum_

101, 416–422 (2014). Article  ADS  CAS  Google Scholar  * Masuda, J. _et al_. The 3He/4He ratio of the new internal He Standard of Japan (HESJ). _Geochem. J._ 36, 191–195 (2002). Article 

Google Scholar  Download references ACKNOWLEDGEMENTS We thank James Jolly, Mario Williamson, James Babinec and Luis Dasilveira for their helpful assistance with the prototype. We have

benefited from advice and encouragement given by Dr. Gerardo A. Brucker of MKS Instruments, Inc., Granville-Phillips Division. We also thank the two anonymous expert reviewers for comments

that improved the manuscript. The MKS Spectra high-resolution quadrupole mass spectrometer was kindly made available to us by MKS Instruments, Inc. Partial support was provided by a seed

grant to G. M. McMurtry and D. R. Hilton from the DECADE program of the Deep Carbon Observatory, Reservoirs and Fluxes, Carnegie Institute for Research, sponsored by the Alfred P. Sloan

Foundation. Additional support was provided by a grant from the US Geological Survey Innovation Center and from the Volcano Science Center. We thank Shaul Hurwitz, Sara Peek, Debra Bergfeld

and Andrew Hunt of the USGS for their field and lab assistance at Mammoth and Kilauea. This is SOEST Contribution no. 10668. AUTHOR INFORMATION Author notes * David R. Hilton is deceased.

AUTHORS AND AFFILIATIONS * Department of Oceanography, School of Ocean and Earth Science and Technology, University of Hawaii, Manoa, Honolulu, HI, 96822, USA Gary M. McMurtry * Fusion

Energy Solutions of Hawaii, 611 University Avenue, Apt. 301, Honolulu, HI, 96826, USA James R. DeLuze * Scripps Institution of Oceanography, University of California, San Diego, 9500 Gilman

Drive, La Jolla, CA, 92093-0244, USA David R. Hilton * MKS Instruments, Inc., Mass Spectrometry Solutions, 3635 Peterson Way, Santa Clara, CA, 95054, USA James E. Blessing Authors * Gary M.

McMurtry View author publications You can also search for this author inPubMed Google Scholar * James R. DeLuze View author publications You can also search for this author inPubMed Google

Scholar * David R. Hilton View author publications You can also search for this author inPubMed Google Scholar * James E. Blessing View author publications You can also search for this

author inPubMed Google Scholar CONTRIBUTIONS G.M. McMurtry designed the study and prepared the original manuscript. J.R. DeLuze assisted in the experiments, instrument design and corrected

the text. D.R. Hilton provided technical oversight and corrected the text. J.E. Blessing provided the M.K.S. quadrupole M.S. and run software. All authors discussed the results and commented

on the manuscript. CORRESPONDING AUTHOR Correspondence to Gary M. McMurtry. ETHICS DECLARATIONS COMPETING INTERESTS Two of the co-authors, G. M. McMurtry and J. R. DeLuze, have a US utility

patent issued as US 10,005,033 B2, “Isotopic enrichment of helium-3 through glass” on June 26, 2018. Co-author J. E. Blessing represents the Mass Spectrometry Solutions section of MKS

Instruments, Inc., which may have a financial interest in the outcomes of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFO. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the

article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use

is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE McMurtry, G.M., DeLuze, J.R., Hilton, D.R. _et al._ Differential Diffusion of

Helium Isotopes in Glass, Quantum-tunneling 3He Enrichment, and Portable 3He/4He Monitoring of Mantle Processes. _Sci Rep_ 9, 5213 (2019). https://doi.org/10.1038/s41598-019-41360-5 Download

citation * Received: 05 November 2018 * Accepted: 04 March 2019 * Published: 26 March 2019 * DOI: https://doi.org/10.1038/s41598-019-41360-5 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative