News Reader.info

ABSTRACT To investigate long length scale structures using neutron scattering, real space techniques have shown certain advantages over the conventional methods working in reciprocal space.

As one of the real space measurement techniques, spin echo modulated small angle neutron scattering (SEMSANS) has attracted attention, due to its relaxed constraints on sample environment

and the possibility to combine SEMSANS and a conventional small angle neutron scattering instrument. In this report, we present the first implementation of SEMSANS at a pulsed neutron source

and discuss important corrections to the data due to the sample absorption. These corrections allow measurements made with different neutron wavelengths and SEMSANS configurations to be

overlaid and give confidence that the measurements provide an accurate representation of the density correlations in the sample. SIMILAR CONTENT BEING VIEWED BY OTHERS SMALL-ANGLE X-RAY AND

NEUTRON SCATTERING Article 12 October 2021 NUCLEAR PHASE RETRIEVAL SPECTROSCOPY USING RESONANT X-RAY SCATTERING Article Open access 31 March 2025 OPTIMIZING THE DYNAMIC PAIR DISTRIBUTION

FUNCTION METHOD FOR INELASTIC NEUTRON SPECTROMETRY Article 03 March 2023 INTRODUCTION Small angle scattering (SAS), using either X-ray or neutrons, has made important measurements of the

structures of many materials including polymers1, magnetic materials2 and biological materials3, addressing length scales from 1 nm to several hundreds of nm. SAS works in reciprocal space

and measures the deflection of collimated radiation away from its initial trajectory4,5,6,7,8. Hence it becomes more and more challenging as the scattering angle decreases. For neutrons, the

neutron spin provides us with another option to label the neutron’s trajectory change with high precision. In a given magnetic field, the neutron spin will execute a motion called Larmor

precession9, and the accumulated Larmor phase is given by $${\rm{\Phi }}=\frac{\gamma m}{h}\lambda {\int }_{path}\,Bdl\propto FI\cdot \lambda ,$$ where _γ_ is the gyromagnetic ratio of the

neutron, _m_ is its mass, _h_ is the Planck constant, _λ_ is the neutron wavelength and _FI_ is the field integral along the neutron trajectory. Using a neutron spin analyzer, the projection

of the polarization vector that is parallel to the analyzing direction can be selected and analyzed, yielding the cosine of the Larmor phase \(P=\,\cos \,{\rm{\Phi }}\). Any technique that

can correlate the change in the neutron energy or momentum with Φ is called neutron Larmor labeling. The first technique of this type was introduced by F. Mezei in 197210, called neutron

spin echo (NSE). It is typically used to label the neutron energy change in quasi-elastic scattering with high resolution. To label the neutron momentum or trajectory change in elastic

neutron scattering, two methods have been implemented, spin echo small angle neutron scattering (SESANS)11 and spin echo modulated small angle neutron scattering (SEMSANS)12,13,14,15. Though

the similarities and difference between these two techniques have been discussed before14, some important details about data analysis, especially for time-of-flight (TOF) measurements, have

not been discussed. The magnetic field boundary of NSE is perpendicular to the beam direction, which means the Larmor phase is not sensitive to any trajectory change to the first oder. The

principle of SESANS is to introduce a tilted magnetic field boundary with different field directions on the two sides of the field boundary to introduce the sensitivity to the neutron

trajectory change16. There are several ways to implement the tilted field boundary, including radio frequency (RF) flippers17, permalloy films18 and magnetic Wollaston prisms

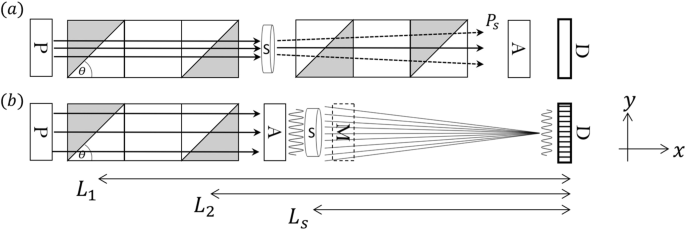
(WP)19,20,21,22. Taking the WP as an example, the SESANS setup is shown in Fig. 1(a). The magnetic field configurations after the sample are flipped compared with the fields before the

sample. With this setup, it is possible to measure the difference of the Larmor phase accumulated before and after the sample. When there is no scattering, no difference in phase will be

measured thus no polarization change will be observed on the detector. But when scattering occurs within the sample, the trajectory after the sample will deviate from its initial path such

that the field integral cannot be balanced any more and hence a net polarization change will be measured. $${P}_{n}(\xi )=\frac{{P}_{s}(\xi )}{{P}_{b}(\xi )}={e}^{\sigma t(G(\xi )-1)}$$ (1)

$$G(\xi )=\frac{1}{\sigma {k}_{0}^{2}}{\int }_{{Q}_{\min }}^{{Q}_{\max }}\frac{d\sigma }{d{\rm{\Omega }}}(Q)\cos \,({Q}_{y}\xi )d{Q}_{y}d{Q}_{z}$$ (2) $$\sigma =\frac{1}{{k}_{0}^{2}}{\int

}_{{Q}_{\min }}^{{Q}_{\max }}\,\frac{d\sigma }{d{\rm{\Omega }}}(Q)d{Q}_{y}d{Q}_{z}$$ (3) The measured polarization of SESANS is well-known as equation (1), where _P__b_, _P__s_ are the

polarization measured with the blank to remove the instrumental errors and sample respectively. _ξ_ is termed spin echo length, which is the length scale accessed in real space. _t_ and _k_0

denote the sample thickness and incoming neutron wave vector respectively. _G_(_ξ_) is the correlation function of the sample, as given in equation (2), which basically is the cosine

Fourier transform of the differential scattering cross section \(\frac{d\sigma }{d{\rm{\Omega }}}(Q)\) with Q being the momentum transfer of neutrons. _Q__min_,_max_ provides the _Q_ range

where the Fourier transform is performed for a real instrument. _σ_ denotes the single neutron scattering cross section, given in equation (3). So SESANS is a 1-D real space technique and it

provides a one to one relation between the density correlation function of the sample and the neutron polarization observed after Larmor labeling. Clearly, any neutron absorbed by the

sample would not contribute to the measured polarization, or to the value of _G_(_ξ_). SESANS is only sensitive to the direction parallel to the gradient of the magnetic field integral (_y_

direction in Fig. 1). As shown by Rekveldt23, both SESANS and SEMSANS will directly yield the pair correlation function even for strongly scattering samples with significant multiple

scattering. This makes them extremely useful for systems with strong scattering to measure inter-particle correlations. This is different from that of SANS, which is typically used for

dilute systems for form factor measurements. PRINCIPLE OF SPIN ECHO MODULATED SMALL ANGLE NEUTRON SCATTERING For SEMSANS, as shown in Fig. 1(b), half the number of Wollaston prisms required

for SESANS are used, with the second WP generating a higher field (_B_2) than the first one (_B_1). Due to the field difference between the two WPs, the Larmor phase (Φ) varies across the

transverse direction (_y_) of the neutron beam, which will introduce a modulation of polarization vectors as \(P(y)=\,\cos \,{\rm{\Phi }}(y)\). After going through the polarization analyzer,

an intensity modulation will be observed on the detector. Due to the divergence of the neutron beam, the modulation might have low visibility. However, by satisfying _B_1_L_1 = _B_2_L_2

with _L_1 and _L_2 being the distances of the WPs to the detector, the induced Larmor phase dispersion on every single point of the detector can be minimized such that a high visibility

intensity modulation can be obtained14. As shown in Fig. 1(b), due to the scattering of the sample, the neutron trajectories will be deviated from their initial paths such that the

visibility of the modulation will be lowered because each pixel on the detector will capture neutrons scattered from different points on the sample14. When tracing back from a specific pixel

of the detector, neutrons with different momentum transfers will be detected and thus Fourier transformed by the modulation, as shown in Fig. 1(b). The trajectory change is encoded and

reflected as a change in the amplitude of the intensity modulation measured by the detector, instead of as a polarization change in SESANS. The ratio of the modulation amplitudes for a

sample and a blank with the same absorption, _A__s_ and _A__b_ respectively, is given by equation (4). The accessible spin echo length in this case is given by \(\xi =\frac{\lambda \omega

{L}_{s}}{2\pi }\) with _ω_ being the frequency of the spatial modulation and _L__s_ being the distance from the sample to the detector, as given in Fig. 1(b). For SEMSANS, polarization is

just a way to produce the intensity modulation at the detector. Therefore, any technique that can produce an intensity modulation can be used for similar purposes. For example, a Talbot-Lau

interferometer with gratings has also been demonstrated to measure the correlation function of a sample13. $${A}_{n}(\xi )=\frac{{A}_{s}}{{A}_{b}}={e}^{\sigma t(G(\xi )-1)}$$ (4) Unlike

SESANS, where sample absorption does not affect the neutron polarization, the absorption of the sample will cause damping of the intensity modulation of SEMSANS. This is especially

troublesome for TOF SEMSANS, where the wavelength dependence of the absorption efficiency will contribute to the correlation function measured, if not considered properly. Though preliminary

data of TOF SEMSANS has been reported in ref.12, the data reproducibility with different magnetic fields is missing and the discussion of the absorption correction is still vague, which

makes it difficult to implement on a real instrument. Since the polarization analyzer can be placed before the sample, a method of combining SANS and SEMSANS24 has been proposed to use the

neutrons usually wasted at the beam stop to further increase the accessible length scales. As the first step, it is critical to have a way of correcting the SEMSANS data such that the

wavelength-dependent absorption efficiency can be removed properly. For SESANS or SEMSANS, equation (1) is true only when all the scattering from the sample can be collected such that a full

Fourier transform from _Q__min_ = 0 to _Q__max_ = ∞ in equation (2) can be obtained. In practice, this is difficult mainly due to: (1) the limited aperture of the detector or polarization

analyzer and (2) the limited acceptance solid angle of the encoding devices. On the other hand, for SEMSANS, the Q range is mainly restricted by (1) the distance of the detector to the

sample, (2) the size of the sample and (3) the divergence of the incident neutron beam. With an infinitely large sample or source, every single point of the detector will provide the same

correlation function. However, for a real sample of finite size, part of the scattering may be missing. This will cause a spatial dependence of the Q range coverage across the detector. So

it is important to keep this in mind when designing an experiment. Since the Q range coverage for SEMSANS has been qualitatively presented and discussed in ref.25, in this report, we will

only show the correction of the SEMSANS data due to the sample absorption, assuming the Fourier transform is relatively complete, which is reasonable since the intensity of the scattering

drops down quickly towards higher Q. The issue regarding the range of the Fourier transform will be discussed quantitatively in a latter article. PRINCIPLE OF ABSORPTION CORRECTION FOR

SEMSANS Following equation (4), the ideal way of conducting a SEMSANS measurement is to introduce a blank sample with the same absorption efficiency but no scattering as the sample of

interest. But in reality, it is difficult and sometime impossible to find such a blank sample. So in many cases, a blank, such as air or solvent, is preferred. For a sample with different

absorption efficiency from the blank, the measured amplitude of the modulation of the sample needs to be renormalized by its absorption efficiency as, $${A}_{n}(\xi

)=\frac{{A}_{s}}{T{A}_{b}}$$ (5) _T_ denotes the attenuation efficiency of the sample with respect to the blank. To measure _T_, the best approach is to introduce a neutron monitor right

after the sample to measure all the neutrons passing through the sample and blank such that $$T=\frac{{N}_{s}(\lambda )}{{N}_{b}(\lambda )},$$ where _N__s_,_b_ are the neutron counts for

sample and blank respectively. For some results we have measured, which will be discussed in the following section, no monitor was implemented. Instead, we used the same position sensitive

detector used for the measurement of the intensity modulation. We sum up the two spin states and integrate the whole detector to obtain _T_ as

$$T=\frac{{N}_{+,s}+{N}_{-,s}}{{N}_{+,b}+{N}_{-,b}},$$ where the superscript “+” and “−” denote the two spin states and _b_, _s_ denote the blank and sample respectively. This method will

give the correct result provided the active area of the detector is large enough to capture all of the attenuated direct beam and the small-angle scattering. The data corrected with these

two approaches will be shown and compared in the following section. When conducting a SEMSANS experiment, to eliminate the inhomogeneity of the beam profile, the intensity modulation of both

neutron spin states (+, −) instead are measured as \({I}_{b,s}(y)=\pm \,{A}_{b,s}\,\sin (\omega y+\varphi )+{\bar{I}}_{b,s}\) and “+” is involved due to the opposite polarization between

the two spin states. _A_ and \(\bar{I}\) are the amplitude and shim intensity of the spatial modulations respectively. By performing \(P=\frac{{N}_{+}-{N}_{-}}{{N}_{+}+{N}_{-}}\), a map of

the polarization modulation can be reconstructed with no dependence on the beam profile as \({P}_{b,s}=\frac{{A}_{b,s}}{{\bar{I}}_{b,s}}\,\sin (\omega y+\varphi )\). The amplitude of the

polarization modulation, which is the same as the visibility of the intensity modulation, is given as \({V}_{b,s}=\frac{{A}_{b,s}}{{\bar{I}}_{b,s}}\). Using these terms, equation (5) can be

rewritten as $${A}_{n}=\frac{{A}_{s}}{T{A}_{b}}=\frac{1}{T}\frac{{V}_{s}{\bar{I}}_{s}}{{V}_{b}{\bar{I}}_{b}}=\frac{{V}_{s}{\rm{\Gamma }}}{{V}_{b}T}$$ (6) _V__s_ and _V__b_ can be obtained by

performing a sinusoidal fit. Γ is the ratio of the shim intensity between the sample and the blank, i.e. \({\rm{\Gamma }}=\frac{{\bar{I}}_{s}}{{\bar{I}}_{b}}\), which can be obtained by

summing up the two spin states over the area where the intensity modulation on the detector is analyzed. The area of interest does not have to be the area of the main beam indicated by the

yellow box in Fig. 2. Instead, it could be smaller than the yellow box providing the sinusoidal fit is reasonably good. Differently, _T_ is obtained by integrating the neutrons over the

whole detector or by using a monitor placed directly behind the sample, as shown in 1(b). Also, the typical way of obtaining _V__s_, _V__b_ is to extract the amplitude of the sinusoidal fit

for a given modulation. Another option is to use standard deviation (SD) of the modulation as a quick way to evaluate the data. In the following section, the analysis with standard deviation

will be performed and compared with fitting. SEMSANS EXPERIMENT AT LARMOR WITH A PULSED BEAM The experiments were conducted on the LARMOR beamline of the ISIS Neutron and Muon Source based

at the Rutherford Appleton Laboratory in Oxfordshire, UK. Superconducting magnetic Wollaston prisms20, instead of the usual RF flippers installed on LARMOR, were used to generate the

intensity modulations on the detector. For the following discussions, there are two experiments involved, labeled as 2016 and 2018. The samples for both experiments are 1 _mm_ thick of

colloidal monodisperse spherical poly(methyl methacrylate) (PMMA) nanoparticles dispersed in deuterated _d_8-dodecane with a volume fraction of 40%. The surfaces of the PMMA particles are

coated with a (12-hydroxystearic acid) PHSA polymer brush to prevent aggregation26. The blank used for the normalization of both experiments is air. To measure the intensity modulation, a

micro-channel plate detector27 was used in TOF mode. The spatial resolution of the detector is 55 _μ_m over an active area of 28 × 28 mm27. Two different analyzers were used during these two

measurements. For 2016, a 3 He analyzer was used and placed after the sample to provide a uniform analyzing power for all the neutron trajectories. For 2018, a supermirror analyzer was

used, which was placed before the sample to avoid the nonuniformity of the analyzing power. The collimation of the beam was defined with two pin holes separated by ~5 _m_ with one upstream

(20 _mm_ × 20 _mm_) and one just in front of the sample (10 _mm_ × 10 _mm_). For both measurements, the tuning of _B_1_L_1 = _B_2_L_2 was achieved by scanning the ratio

\((r=\frac{{B}_{1}}{{B}_{2}})\) while keeping the difference (_B_1 − _B_2) the same. Benefiting from the multiple wavelengths available at LARMOR, a wide range of spin echo length can be

accessed simultaneously at a single setting of magnetic fields in the WPs. Figure 2 shows the intensity modulations of one of the spin states obtained in the 2018 measurements at neutron

wavelength of 6.27 Å. As discussed before, both spin states are measured to eliminate any possible nonuniformity of the beam spatial profile. Then the polarization modulation is integrated

vertically along _z_ within the yellow box for each wavelength. The 1D polarization plots for all the wavelengths are then stacked together into a 2D map for both the air and PMMA, as given

in Fig. 3. The vertical centering of the modulation in Fig. 3 can be shifted by tuning the current in the rectangular field between the WPs. While the modulation in Fig. 3(a) is sharp and

clean, the scattering from the PMMA sample will smear out its visibility, as shown in Fig. 3(b). As the wavelength increases, the modulation will be smeared out more. For each wavelength,

both the fit and the standard deviation (SD) are used to obtain \(\frac{{V}_{s}}{{V}_{b}}\) for the data correction. DATA CORRECTION WITH THE POSITION SENSITIVE DETECTOR For the 2016

experiment, the measurements were conducted at five different magnetic field settings, which are listed in the Fig. 4. The quantity \(\frac{\mathrm{ln}({A}_{n})}{{\lambda }^{2}\cdot t}\) is

plotted such that the wavelength dependence of the total scattering can be removed28. As one can see from Fig. 4(a), these curves at different settings of field do not overlap with each

other, especially at the shortest spin echo length. This is due to the usage of different wavelength bands to achieve the same spin echo length with different settings of fields. During the

experiment, no monitor was implemented after the sample, so the intensity on the whole detector was integrated and used to obtain _T_, as labeled by PSD in the figure. After being corrected

by equation (6), the measurements with different experimental settings in Fig. 4(b) overlap with each other. The PMMA system is well understood and the average diameter of the PMMA particles

can be approximately given by the first crossing point of the curve with its saturation level, which is 215 _nm_26. This is very close to the hydrodynamic diameter of the particles (200 

_nm_) obtained from dynamic light scattering. Also, the feasibility of using the standard deviation for the calculation of the correlation function is also evaluated. As we can see from Fig.

 4(b), after correction, the measurements at the different magnetic fields and sample-to-detector distance overlap with each other well when the modulation amplitudes are obtained by fitting

the data to a sinusoidal function. For the same field setting, the spread of the data points is larger compared when the fitted amplitudes are replaced by the standard deviation of the

modulation. While the error for a measurement with poor statistics can be lowered by forcing the data to comply with a specific fit function, the method of standard deviation assumes no

correlation between the data points and thus comes with a larger error. Also due to the poor statistics at longer wavelength, the error of the data contributes too much to the standard

deviation of the data, which makes it too noisy to use standard deviation. Nevertheless, as an easy and quick way to check the data, standard deviation is still useful provided the

statistics of the measurements are adequate. DATA CORRECTION WITH THE MONITOR To verify the effectiveness of correcting the data by integrating the detector to obtain _T_, the same

experiment was repeated in 2018 with a neutron monitor employed right after the sample. When the SEMSANS measurements were finished, the relative attenuation efficiency of the sample was

measured again with respect to the blank using the monitor. The monitor is made of neutron active scintillator, which was designed to sample a high flux, homogenous neutron beam. As shown in

Fig. 5(a) plot is corrected with _T_ obtained by integrating the whole detector, the same as the previous section. Since the experiments were conducted two years later compared with Fig. 5,

to our knowledge, the correlation function of the two measurements may differ from one another due to, for example, the aging or aggregation of the PMMA particles. Figure 5(b) is corrected

with _T_ obtained using the monitor. For both cases, the curves at different field settings overlap with each well. The difference is observed in the level of the curves at large spin echo

lengths. The data corrected with the detector shows higher values, which means the measured total scattering of the sample is lower if we have to correct the data with the detector. Figure 6

shows the value of _T_ measured by either integrating the whole detector or the monitor. Since the scattering angle increases as wavelength, more neutrons with long wavelength will fall off

the detector of limited size than at short wavelength. Therefore the value _T_ measured by the monitor is consistently higher especially for long wavelength neutrons and yields a lower

value of \(\frac{{\rm{\Gamma }}}{T}\), compared with that of the data measured by integrating the whole detector. This is mainly due to the difference of the solid angle coverage between the

PSD and the monitor. Since the PSD is much further away, it will cover a smaller solid angle, which will miss more of the scattered neutrons especially for long wavelength neutrons. With a

higher value of \(\frac{{\rm{\Gamma }}}{T}\), a higher level of the curve would be expected from \(\frac{\mathrm{ln}({A}_{n})}{{\lambda }^{2}\cdot t}\) as shown in Fig. 5. Since the level of

the curve at long spin echo length is given by _σ_ = _λ_2_t_Δ_ρ_2_ϕ_(1−_ϕ_)_ζ_, where _t_ is the sample thickness, Δ_ρ_ is the difference in scattering length densities between the

particles and solvent _ϕ_ is the volume fraction and _ζ_ denotes the characteristic length scale of the sample. This means for the measurements where this level matters, using the detector

with a restricted size can result in a wrong answer. While for the measurements, where only the correlation distance of the particles matters, either method can be used. To make sure one can

always get the best results, a monitor is always preferred right after the sample. DISCUSSION We have discussed the feasibility of correcting the SEMSANS data to remove the contribution

from the difference of the absorption efficiency between the sample and blank. The data correction is especially critical for TOF SEMSANS due to the wavelength dependence of the absorption

efficiency. By employing the correction, the correlation function measured at various settings of spin echo length can overlap with each other. Though a monitor is always preferred for the

measurement of the attenuation efficiency of the sample, the same high spatial resolution detector, used for the measurement of the modulation, can also be used provided its area is large

enough to capture all the small angle scattered beam. But in reality, a detector with a combination of high spatial resolution and large active size is always difficult. The correction

method we have described is also applicable to any other scattering technique based on the intensity modulation, including the Talbot-Lau method and modulated intensity with zero effort

(MIEZE) for quasi-elastic scattering. For the Fourier transform of both SESANS or SEMSANS, the effect of limited Q range will be presented later. For the correction method discussed here, we

are assuming the scattering is purely elastic and the neutrons will maintain their energy. But for some samples, the neutrons might gain or lose energy by inelastic scattering with the

sample, which is also known as thermalization or moderation. It has been shown that, the thermalization process of cold neutrons within a liquid such as H2O will accelerate neutrons, causing

unexpected faster neutrons29. The percentage of the thermalized neutrons will increase with neutron wavelength. This means that shorter wavelength neutrons may be preferable for experiments

with samples that are good moderators such as H2O. REFERENCES * Kimata, S. _et al_. Molecular basis of the shish-kebab morphology in polymer crystallization. _Sci._ 316, 1014–1017,

https://doi.org/10.1126/science.1140132 (2007). Article  CAS  ADS  Google Scholar  * Mühlbauer, S. _et al_. Skyrmion lattice in a chiral magnet. _Sci._ 323, 915 (2009). Article  ADS  Google

Scholar  * Stuhrmann, H. Neutron small-angle scattering of biological macromolecules in solution. _J. Appl. Crystallogr._ 7, 173–178, https://doi.org/10.1107/S0021889874009071 (1974).

Article  CAS  Google Scholar  * Dewhurst, C. D. _et al_. The small-angle neutron scattering instrument D33 at the Institut Laue–Langevin. _J. Appl. Crystallogr._ 49, 1–14,

https://doi.org/10.1107/S1600576715021792 (2016). Article  CAS  Google Scholar  * Heller, W. T. _et al_. The suite of small-angle neutron scattering instruments at Oak Ridge National

Laboratory. _J. Appl. Crystallogr._ 51, 242–248, https://doi.org/10.1107/S1600576718001231 (2018). Article  CAS  Google Scholar  * Sokolova, A. _et al_. Performance and characteristics of

the BILBY time-of-flight small-angle neutron scattering instrument. _J. Appl. Crystallogr._ 52, 1–12, https://doi.org/10.1107/S1600576718018009 (2019). Article  CAS  Google Scholar  *

Jaksch, S. _et al_. Concept for a time-of-flight small angle neutron scattering instrument at the european spallation source. _Nucl. Instruments Methods Phys. Res. Sect. A: Accel.

Spectrometers, Detect. Assoc. Equip_. 762, 22–30 http://www.sciencedirect.com/science/article/pii/S0168900214004203, https://doi.org/10.1016/j.nima.2014.04.024 (2014). Article  CAS  ADS 

Google Scholar  * Feoktystov, A. V. _et al_. KWS-1 high-resolution small-angle neutron scattering instrument at JCNS: current state. _J. Appl. Crystallogr._ 48, 61–70,

https://doi.org/10.1107/S1600576714025977 (2015). Article  CAS  Google Scholar  * Bloch, F. Nuclear induction. _Phys. Rev._ 70, 460–474 (1946). Article  CAS  ADS  Google Scholar  * Mezei, F.

Neutron spin echo: A new concept in polarized thermal neutron techniques. _Zeitschrift für Physik_ 255, 146–160, https://doi.org/10.1007/BF01394523 (1972). Article  CAS  ADS  Google Scholar

  * Rekveldt, M. T. Novel sans instrument using neutron spin echo. _Nucl. Instruments Methods Phys. Res. Sect. B: Beam Interactions with Mater. Atoms_ 114, 366–370,

https://doi.org/10.1016/0168-583X(96)00213-3 (1996). Article  CAS  ADS  Google Scholar  * Strobl, M. _et al_. Tof-semsans-time-of-flight spin-echo modulated small-angle neutron scattering.

_J. Appl. Phys._ 112, 014503, https://doi.org/10.1063/1.4730775 (2012). Article  CAS  ADS  Google Scholar  * Strobl, M. _et al_. Using a grating analyser for semsans investigations in the

very small angle range. _Phys. B: Condens. Matter_ 407, 4132–4135, https://doi.org/10.1016/j.physb.2012.06.036 (2012). Article  CAS  ADS  Google Scholar  * Li, F. _et al_. Spin echo

modulated small-angle neutron scattering using superconducting magnetic wollaston prisms. _J. Appl. Crystallogr._ 49, 55–63, https://doi.org/10.1107/S1600576715021573 (2016). Article  CAS 

Google Scholar  * Strobl, M. _et al_. Quantitative neutron dark-field imaging through spin-echo interferometry. _Sci. Reports_ 5, 16576, https://doi.org/10.1038/srep16576 (2015). Article 

CAS  ADS  Google Scholar  * Pynn, R. Neutron spin-echo and three-axis spectrometers. J. Phys. E: Sci. Instruments 11, 1133, http://stacks.iop.org/0022-3735/11/i=11/a=015 (1978). Article  CAS

  ADS  Google Scholar  * Plomp, J. _Spin-echo development for a time of flight neutron reflectometer_. Thesis (2009). * Bouwman, W. G., Kraan, W. & Rekveldt, M. T. Spin echo small angle

neutron scattering experiment. _Phys. B: Condens. Matter_ 267–268, 79–83, https://doi.org/10.1016/S0921-4526(99)00031-9 (1999). Article  ADS  Google Scholar  * Parnell, S. R. _et al_. Spin

echo small angle neutron scattering using a continuously pumped 3he neutron polarisation analyser. _Rev. Sci. Instruments_ 86, 023902, https://doi.org/10.1063/1.4909544 (2015). Article  CAS

  ADS  Google Scholar  * Li, F. _et al_. Superconducting magnetic wollaston prism for neutron spin encoding. _Rev. Sci. Instruments_ 85, 053303, https://doi.org/10.1063/1.4875984 (2014).

Article  CAS  ADS  Google Scholar  * Li, F. _Larmor labeling of neutron spin using superconducting Wollaston prisms_. Thesis (2016). * Li, F., Parnell, S. R., Wang, T., Baxter, D. V. &

Pynn, R. Magnetic field optimization and design of a superconducting neutron wollaston prism. _J. Physics: Conf. Ser._ 711, 012015 (2016). Google Scholar  * Rekveldt, M. T. _et al_. _Elastic

Neutron Scattering Measurements Using Larmor Precession of Polarized Neutrons_, 87–99, https://doi.org/10.1007/3-540-45823-9_9 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2003).

Chapter  Google Scholar  * Bouwman, W. G., Duif, C. P., Plomp, J., Wiedenmann, A. & Gähler, R. Combined sans–sesans, from 1 nm to 0.1 mm in one instrument. _Phys. B: Condens. Matter_

406, 2357–2360, http://www.sciencedirect.com/science/article/pii/S0921452610011348. https://doi.org/10.1016/j.physb.2010.11.069. Proceedings of the 8th International Workshop on Polarised

Neutrons for Condensed Matter Investigation (2011). Article  CAS  ADS  Google Scholar  * Kusmin, A., Bouwman, W. G., vanWell, A. A. & Pappas, C. Feasibility and applications of the

spin-echo modulation option for a small angle neutron scattering instrument at the european spallation source. _Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect.

Assoc. Equip._ 856, 119–132, https://doi.org/10.1016/j.nima.2016.12.013 (2017). Article  CAS  ADS  Google Scholar  * Washington, A. L. _et al_. Inter-particle correlations in a hard-sphere

colloidal suspension with polymer additives investigated by spin echo small angle neutron scattering (sesans). _Soft Matter_ 10, 3016–3026, https://doi.org/10.1039/C3SM53027B (2014). Article

  CAS  PubMed  ADS  Google Scholar  * Tremsin, A. S. _et al_. Detection efficiency, spatial and timing resolution of thermal and cold neutron counting mcp detectors. _Nucl. Instruments

Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip._ 604, 140–143, https://doi.org/10.1016/j.nima.2009.01.041 (2009). Article  CAS  ADS  Google Scholar  * Andersson, R.,

van Heijkamp, L. F., de Schepper, I. M. & Bouwman, W. G. Analysis of spin-echo small-angle neutron scattering measurements. _J. Appl. Crystallogr._ 41, 868–885,

https://doi.org/10.1107/S0021889808026770 (2008). Article  CAS  Google Scholar  * Do, C. _et al_. Understanding inelastically scattered neutrons from water on a time-of-flight small-angle

neutron scattering (sans) instrument. _Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip_. 737, 42–46,

http://www.sciencedirect.com/science/article/pii/S0168900213015696, https://doi.org/10.1016/j.nima.2013.11.030 (2014). Article  CAS  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS

We would like to acknowledge Gøran Nilsen and Mark Devonport for their support with the 3He system, Freddie Akeroyd, Winfried Kockelmann and Anton Tremsin for their support with the MCP

detector. We are also grateful to Andrew Schofield for the preparation of the PMMA sample. The authors would like to thank the United Kingdom Science and Technology Facilities Council (STFC)

for the award of beam time. FL also would like to acknowledge the support from Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the US Department of Energy. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Neutron Sciences Directorate, Oak Ridge National Laboratory, Oak Ridge, TN, 37830, USA Fankang Li & Roger Pynn * Faculty of Applied Sciences, Delft

University of Technology, Mekelweg 15, Delft, JB 2629, The Netherlands Steven R. Parnell & Jeroen Plomp * ISIS Pulsed Neutron and Muon Source, STFC, Rutherford Appleton Laboratory,

Chilton, Oxon, OX11 0QX, UK Robert Dalgliesh & Adam Washington * Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN, 47408, USA Roger Pynn Authors * Fankang

Li View author publications You can also search for this author inPubMed Google Scholar * Steven R. Parnell View author publications You can also search for this author inPubMed Google

Scholar * Robert Dalgliesh View author publications You can also search for this author inPubMed Google Scholar * Adam Washington View author publications You can also search for this author

inPubMed Google Scholar * Jeroen Plomp View author publications You can also search for this author inPubMed Google Scholar * Roger Pynn View author publications You can also search for

this author inPubMed Google Scholar CONTRIBUTIONS F.L. conducted the experiment, came up with the data correction method and prepared the manuscript. S.R.P., R.D. and A.W. conducted the

experiment and contributed to the data correction method. J.P. contributed to experiment and the data correction method. R.P. conceived and conducted the experiments and contributed to the

data correction method. All authors reviewed the manuscript. CORRESPONDING AUTHOR Correspondence to Fankang Li. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing

interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Li, F., Parnell,

S., Dalgliesh, R. _et al._ Data Correction of Intensity Modulated Small Angle Scattering. _Sci Rep_ 9, 8563 (2019). https://doi.org/10.1038/s41598-019-44493-9 Download citation * Received:

04 January 2019 * Accepted: 25 April 2019 * Published: 12 June 2019 * DOI: https://doi.org/10.1038/s41598-019-44493-9 SHARE THIS ARTICLE Anyone you share the following link with will be able

to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative