News Reader.info

ABSTRACT When two magnetic skyrmions – whirl-like, topologically protected quasiparticles – form a bound pair, a biskyrmion state with a topological charge of _N_Sk = ±2 is constituted.

Recently, especially the case of two partially overlapping skyrmions has brought about great research interest. Since for its formation the individual skyrmions need to posses opposite

in-plane magnetizations, such a biskyrmion cannot be stabilized by the Dzyaloshinskii-Moriya-interaction (DMI), which is the interaction that typically stabilizes skyrmions in

non-centrosymmetric materials and at interfaces. Here, we show that these biskyrmions can be stabilized by the dipole-dipole interaction in centrosymmetric materials in which the DMI is

forbidden. Analytical considerations indicate that the bound state of a biskyrmion is energetically preferable over two individual skyrmions. As a result, when starting from two skyrmions in

a micromagnetic simulation, a biskyrmion is formed upon relaxation. We propose a scheme that allows to control this biskyrmion formation in nanodisks and analyze the individual steps.

SIMILAR CONTENT BEING VIEWED BY OTHERS COLLECTIVE SKYRMION MOTION UNDER THE INFLUENCE OF AN ADDITIONAL INTERFACIAL SPIN-TRANSFER TORQUE Article Open access 24 June 2022 3D QUASI-SKYRMIONS IN

THICK CYLINDRICAL AND DOME-SHAPE SOFT NANODOTS Article Open access 02 March 2022 PARTICLE-SIZE DEPENDENT STRUCTURAL TRANSFORMATION OF SKYRMION LATTICE Article Open access 11 November 2020

INTRODUCTION Magnetic skyrmions1,2,3 are whirl-like magnetic quasiparticles on the sub-micrometer scale, first observed in MnSi2 as periodic arrays (so-called skyrmion crystals or lattices).

Later, also isolated skyrmions have been found in ferromagnetic Fe0.5Co0.5Si films4. Each skyrmion is characterized by a topological charge $${N}_{{\rm{S}}{\rm{k}}}=\frac{1}{4\pi }\int

{\boldsymbol{m}}({\boldsymbol{r}})\cdot [\frac{{\rm{\partial }}{\boldsymbol{m}}({\boldsymbol{r}})}{{\rm{\partial }}x}\times \frac{{\rm{\partial

}}{\boldsymbol{m}}({\boldsymbol{r}})}{{\rm{\partial }}y}]{{\rm{d}}}^{2}r$$ (1) of ±1 [_M_(_R_) is the magnetization], which imposes an energy barrier that protects a skyrmion from

annihilating to the ferromagnetic groundstate. Their high stability and small sizes make skyrmions candidates for the carriers of information in future storage devices5,6. For example,

skyrmions can be written and deleted, driven by electric currents and read in thin films6,7,8,9,10,11. An object which is closely related to the skyrmion is the biskyrmion, a term that

describes two skyrmions in a bound state. Like the skyrmion12 it was initially proposed in nuclear physics13,14. In the context of magnetism the term ‘biskyrmion’ has been used for two

skyrmions in a bilayer quantum Hall system15, for two asymmetric skyrmions in the cone phase of a chiral helimagnet which exhibit an attractive interaction16,17, and – as observed for the

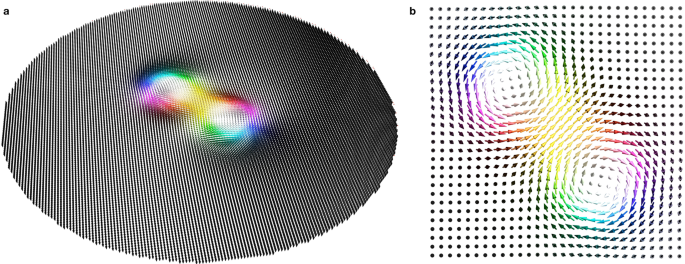
first time in 201418 – a composition of two partially overlapping skyrmions with opposite in-plane magnetizations (Fig. 1b)18,19,20,21,22,23. Still, all of these objects are geometrically

distinct. In the remainder of this paper the term ‘biskyrmion’ refers always to the latter object: a pair of partially overlapping skyrmions with a helicity difference of _π_ that has

attracted an enormous research interest since its initial discovery. Although merged, each skyrmion forming the biskyrmion can still be identified and their shifted centers indicate a merely

partial overlap. For this reason, each skyrmion contributes with its topological charge of ±1 to the biskyrmion’s topological charge of _N_Sk = ±2. Periodic arrays of such biskyrmions

(biskyrmion crystals) have first been observed in the centrosymmetric layered manganite La2−2_x_Sr1+2_x_Mn2O718; other centrosymmetric biskyrmion hosts followed recently19,20,21,22. If

_individual_ biskyrmions could be stabilized, they could be used to store information just like conventional skyrmions. However, up to now, individual biskyrmions have only been predicted in

frustrated magnets23 — even the existence of conventional skyrmions in these materials24,25,26 remains to be proven experimentally. These considerations suggest to investigate

centrosymmetric materials with dominating dipole-dipole interaction, like in the experimental observations of biskyrmion crystals, to find also individual biskyrmions. In these materials the

constituents of biskyrmions — skyrmionic bubbles — have been found already decades ago27,28. In this Paper, we propose a scheme for creating biskyrmions in a controlled manner. In a first

step, we derive an attractive skyrmion-skyrmion interaction which is necessary for the formation of a biskyrmion, using an analytical model. Thereafter, we show by micromagnetic simulations

for a nanodisk geometry that two Bloch skyrmions with opposite in-plane magnetizations can be written at opposite sides of a nanodisk. We simulate the resultant motion of such skyrmions upon

relaxation and derive their equations of motion analytically. After relaxation we find that both skyrmions have merged to a stable biskyrmion state (Fig. 1). The importance of the

skyrmions’ helicities for this process is discussed. We summarize our findings and give an outlook. RESULTS ANALYTICAL SUPERPOSITION OF TWO SKYRMIONS As presented in the introduction, it is

an established fact that non-collinear spin textures like skyrmions can be stabilized by the dipole-dipole interaction3. Therefore, it is well conceivable that also two skyrmions with

reversed in-plane magnetizations can be stabilized in the same sample by this mechanism. The question is now how these skyrmions interact. As we will show, already considering a short-range

approximation of the dipole-dipole interaction leads to the conclusion that the two skyrmions attract each other, thereby allowing to form a biskyrmion. This finding is later confirmed by

micromagnetic simulations where the full dipole-dipole interaction is considered and a biskyrmion state is metastabilized. To find the attractive interaction between two skyrmions with

opposite in-plane magnetizations, we superpose such two (fixed) skyrmions at a distance of Δ_r_ analytically. For simplicity we neglect shape deformations of the skyrmions (such deformations

are accounted for by the micromagnetic simulations later in this paper). The magnetic textures _M_(_R_) = (sinΘcosΦ, sinΘsinΦ, cosΘ) are imposed onto a two-dimensional square lattice with

lattice constant _a_. The spherical coordinates of the magnetic moments of an individual skyrmion read Φ = arctan(_my_/_x_) + _γ_ and \({\rm{\Theta }}=2\arctan

(\sqrt{{x}^{2}+{y}^{2}}/{r}_{0})\); _r_0 determines the size of the skyrmion. The helicity _γ_ of the skyrmion manifests itself in the in-plane components via Φ = _mϕ_ + _γ_. Here, _ϕ_ is

the polar angle of the position vector with respect to the skyrmion’s center and _m_ = +1 is the vorticity, which defines the sense of in-plane spin rotation. In case of a Bloch skyrmion we

have _m_ = 1 and _γ_ = ±_π_/2, i. e., the polar angle of the spin orientation Φ has a fixed offset to the polar angle _ϕ_ of the position _R_ with respect to the skyrmion’s center. The

topological charge _N_Sk = _p_ · _m_ = ±1 of a skyrmion depends on the skyrmion’s polarity _p_ = ±1. In this Paper, we consider skyrmions in a ferromagnetic surrounding, magnetized along

−_z_, which gives a polarity and topological charge of +1. One way to superpose two skyrmions is adding their polar angles and multiplying the arguments of their arctan function for the

azimuthal angle, $$\begin{array}{rcl}{\rm{\Phi }} & = & \arctan \,(\frac{y-{\rm{\Delta }}y/2}{x-{\rm{\Delta }}x/2})+\arctan \,(\frac{y+{\rm{\Delta }}y/2}{x+{\rm{\Delta

}}x/2})+({\gamma }_{d}-\alpha ),\\ {\rm{\Theta }} & = & 2\arctan \,[\frac{1}{{r}_{0}^{2}}\sqrt{{(x-{\rm{\Delta }}x/2)}^{2}+{(y-{\rm{\Delta }}y/2)}^{2}}\cdot \sqrt{{(x+{\rm{\Delta

}}x/2)}^{2}+{(y+{\rm{\Delta }}y/2)}^{2}}].\end{array}$$ (2) The condition |_M_| = 1 holds for all _R_. Here, Δ_R_ = (Δ_x_, Δ_y_, 0) = Δ_r_(cos_α_, sin_α_, 0) is the displacement vector of

the two skyrmions with helicities _γ__d_ and _γ__d_ + _π_. For an inter-skyrmion distance of Δ_r_ ≫ _r_0 we find two isolated skyrmions, for Δ_r_ ≈ 2_r_0 the solution is a biskyrmion state

with two skyrmions overlapping partially, and for Δ_r_ = 0 a higher-order skyrmion is formed. In any case, the total topological charge is _N_Sk = +2. ATTRACTIVE SKYRMION-SKYRMION

INTERACTION We clarify now which term in the lattice Hamiltonian causes an attractive interaction of the two skyrmions, what can lead to the formation of a biskyrmion. The exchange

interaction \({H}_{{\rm{ex}}}=-\,\frac{1}{2}\sum _{ij}\,{J}_{ij}{{\boldsymbol{m}}}_{i}\cdot {{\boldsymbol{m}}}_{j}\) is independent of Δ_r_ and independent of the skyrmions’ sizes and

shapes. Hence, the exchange interaction alone will not stabilize a biskyrmion. This finding is in line with the fact that even conventional skyrmions cannot be stabilized by a bare exchange

interaction, unless further (frustrated) exchange interactions are considered; then, the interaction constants _J__ij_ have different signs for nearest and second-nearest neighbor spins. The

same requirement holds for biskyrmions23. In most materials, skyrmions are stabilized by the Dzyaloshinskii-Moriya interaction (DMI)29,30 \({H}_{{\rm{DMI}}}=\frac{1}{2}\sum

_{ij}\,{{\boldsymbol{D}}}_{ij}\cdot ({{\boldsymbol{m}}}_{i}\times {{\boldsymbol{m}}}_{j})\) that originates from spin-orbit coupling and a broken inversion symmetry. The DMI vectors _D__ij_ 

= −_D__ji_ whose directions are prescribed by the crystal symmetry determine the type of metastable spin texture31. For all types of DMI the energy contributions of the two skyrmions with

reversed in-plane magnetizations — what is necessary for the formation of the here considered biskyrmion — cancel. As a result, _H_DMI is independent of Δ_r_ and does not allow for the

formation of a biskyrmion. Even more detrimental, at least one of the two skyrmions would annihilate in a simulation. An interaction that is present in all magnetic materials, but often

‘overshadowed’ by the DMI in non-centrosymmetric materials, is the dipole-dipole interaction $${H}_{{\rm{dp}}}=-\frac{1}{2}\sum _{ij}\,\frac{{\mu }_{0}}{4\pi

|{{\boldsymbol{r}}}_{ij}{|}^{5}}[3({{\boldsymbol{m}}}_{i}\cdot {{\boldsymbol{r}}}_{ij})({{\boldsymbol{m}}}_{j}\cdot {{\boldsymbol{r}}}_{ij})-{{\boldsymbol{m}}}_{i}\cdot

{{\boldsymbol{m}}}_{j}].$$ (3) In case the DMI is forbidden, like in centrosymmetric materials, this interaction can stabilize not only skyrmions32,33,34,35 but also biskyrmions, as will be

presented later in this paper by micromagnetic simulations. To establish an intuitive understanding of the attractive skyrmion-skyrmion interaction, which is necessary for the formation of a

biskyrmion, we consider a short-range approximation of the dipole-dipole interaction for the calculations in this section. Note however, that this approximation is accompanied by a loss of

information36: Even the lowest energy state of the considered model would relax to a collinear ferromagnetic configuration if only the short-range approximation was considered in a

simulation in which shape relaxation is allowed. Since Derrick’s theorem37 implies the absence of local energy minima for non-collinear spin textures for this reduced type of dipole-dipole

interaction38, we cannot make statements on the metastability of a certain configuration. However, comparing the energies of states described by the model in Eq. (2) allows to extract an

attractive skyrmion-skyrmion interaction. The actual proof of metastability are the micromagnetic simulations of the three-dimensional system with the full dipole-dipole interaction shown

later in this paper. A three-dimensional consideration is essential since non-collinear spin textures are only metastable once the sample is thicker than a critical value28,39. To extract

the attractive interaction we consider in this section only nearest-neighbor interactions in a two-dimensional square lattice. In this case the second term in Eq. (3) merely rescales the

exchange interaction, thereby rendering only the first term relevant $${H}_{{\rm{dp}},{\rm{approx}}}\propto -\,\sum _{ij}\,({{\boldsymbol{m}}}_{i}\cdot

{\hat{{\boldsymbol{r}}}}_{ij})({{\bf{m}}}_{j}\cdot {\hat{{\boldsymbol{r}}}}_{ij}),$$ (4) where \({\hat{{\boldsymbol{r}}}}_{ij}\) is a unit vector which is parallel to either

\({{\boldsymbol{e}}}_{x}\) or \({{\boldsymbol{e}}}_{y}\). This interaction can be interpreted as a special easy-plane anisotropy. It favors parallel spins energetically. Such an alignment is

approximately fulfilled for the overlap region of the two skyrmions (that is the center of the biskyrmion). As a result, two skyrmions in centrosymmetric materials attract each other. We

find that partially overlapping Bloch skyrmions (_γ_ = ±_π_/2) at a displacement angle of _α_ = ±_π_/4 or ±3_π_/4 have the lowest energy of all states described by Eq. (2) with respect to

the short-range approximation of the dipole-dipole interaction. The energy minimum occurs at an inter-skyrmion distance of Δ_r_ ≈ 2_r_0, which is a biskyrmion state (Fig. 2a). The helicity

dependence (Fig. 2b) has a cosine shape making the Bloch skyrmion energetically most favorable. This helicity dependence is not unique to the biskyrmion state; a similar dependence is found

for a single skyrmion. The _α_ dependence (Fig. 2c; global rotation of the texture) originates from the underlying lattice. As a consequence it has a period of _π_/2 with respect to _α_ for

the square lattice. Different lattices have energy minima at other angles, e. g. _α_ = ±_π_/6, ±3_π_/6 and ±5_π_/6 for a hexagonal lattice. So far, we have shown that two skyrmions with

reversed in-plane magnetizations attract each other in centrosymmetric systems without DMI but with dipole-dipole interaction. The resulting biskyrmion is expected to be of Bloch type and to

form at an angle of 45° with respect to the underlying lattice. In the following, micromagnetic simulations will be used to analyze how these two specific skyrmions can be stabilized in a

three-dimensional sample considering the full dipole-dipole interaction. We will show that all three results from the analytic model are confirmed in the simulation: the skyrmions attract

each other to form a biskyrmion characterized by _γ__e_ = ±_π_/2 and _α_ = ±_π_/4, ±3_π_/4. SETUP FOR THE MICROMAGNETIC SIMULATIONS To support the above analytical considerations, we

performed micromagnetic simulations for a thin magnetic nanodisk with out-of-plane anisotropy. These disks have been in the focus of skyrmion-related research in many recent

publications40,41,42,43,44,45. The considered disk and its surfaces exhibit negligibly small DMI, so that only the dipole-dipole interaction (included in the demagnetization field) could

stabilize a biskyrmion. The micromagnetic simulations were performed using the Mumax3 code46,47. Therein, the Landau-Lifshitz-Gilbert equation (LLG)48,49,50 with parameters similar to those

in ref.35 is solved for each discretized magnetic moment _M__i_; see Methods. Initially, two energetically degenerate metastable skyrmions with helicities ±_π_/2 are ‘written’ symmetrically

to the nanodisk’s center. Upon relaxation they are pushed to the center by their attractive interaction and the confinement potential of the nanodisk. When the skyrmions reach the

energetically optimal distance, a biskyrmion has formed. We proceed by discussing the individual steps in detail and begin with the mechanism for writing the skyrmions. GENERATION OF

ISOLATED SKYRMIONS The vanishing DMI complicates a controlled writing of skyrmions in centrosymmetric materials, since there is no energetically preferred chirality: injecting spins oriented

along _Z_ via spin torque, as commonly done in DMI-dominated systems6, produces a topologically trivial bubble (the in-plane spin components point toward the disk’s center; they are

oriented nearly parallel). Evidently, in order to write two skyrmions off-center without DMI the aimed-for texture has to be induced explicitly. In other words, deterministic instead of

stochastic writing has to be considered. This is especially important since the two skyrmions need to have opposite helicities. We consider two smaller disks attached to the nanodisk (Fig. 

3a). These additional disks host stable in-plane vortex configurations51,52, similar to refs.53,54,55,56. The opposite helicities of the vortices, which are switchable e. g., by a magnetic

field57,58,59,60, determine the helicity of the two emerging Bloch skyrmions. If an electric current _J_write is applied in perpendicular direction (here: _J_write = 7 × 108A/cm−2_E__z_

applied for 200 ps), the spin of the flowing electrons is aligned with the vortex (as long as the coupling is sufficiently large) and injected into the underlying nanodisk; there a skyrmion

is formed via spin torque. The writing process is visualized in Fig. 3b–g. Starting from a ferromagnetic state, a skyrmionium-like configuration (a skyrmion with reversed skyrmion-like

magnetization in its center61,62,63) is written (b–d). Since the ‘central’ reversed skyrmion is very small, it quickly annihilates (<100 ps) so that a skyrmion with a topological charge

of _N_Sk = +1 remains at each side of the disk (e). On the time scale of 1ns their sizes relax (f, g). While the writing mechanism considered here appears convenient, other approaches are

suited for an experimental realization as well; in the following, we give an incomplete list. Merons (vortices with out-of-plane spins in their center) in the writing devices work equally

well. The same holds for skyrmions. All of the considered textures have a similar in-plane magnetization which seems to be the most important component for skyrmion generation in

centrosymmetric materials; due to the fact that the dipole-dipole interaction is achiral, a suitable in-plane magnetization has to be ‘imprinted’ in order to ‘generate’ a topological charge.

In a recent publication63 we have presented a mechanism for writing skyrmioniums via a photosensitive switch64: a laser triggers a radial current in a ring of a heavy metal, thereby

generating an in-plane toroidal spin polarization via the spin Hall effect. This toroidal spin profile is then injected into the magnetic nanodisk, very similar to the vortex-writing device

but for a ring geometry instead of a disk geometry. Depending on the chosen parameters, this method works for writing skyrmions as well. The sign of the applied bias voltage controls the

spin polarization’s orientation and thus the writing of either +_π_/2 or −_π_/2 Bloch skyrmions. As a third option, one may consider spatiotemporally tuned electron sources65. The type of

induced Bloch skyrmion can be controlled via the propagation direction of the electrons (beam applied from above or below the nanodisk). MOTION OF A SINGLE SKYRMION Before discussing the

formation of biskyrmions, we address the motion of a single skyrmion within the nanodisk. After relaxation of shape and size, a skyrmion starts to move toward the center of the nanodisk in a

counter-clockwise spiral trajectory (orange in Fig. 4a–c). Initially, the skyrmion is accelerated but is subsequently decelerated when the skyrmion’s center is close to the nanodisk’s

center. The helicity of the skyrmion remains unchanged during the evolution. The spiral trajectory is understood by considering the Thiele equation66,67 $$b\,{\boldsymbol{G}}\times

{\boldsymbol{v}}-b\underline{D}\alpha {\boldsymbol{v}}+{F}_{{\rm{int}}}(r)\frac{{\boldsymbol{r}}}{r}=0.$$ (5) In this effective ‘center-of-mass-like’ description of magnetic quasiparticles

with velocity _V_ all internal degrees of freedom have been integrated out. The spatial details of the skyrmion are ‘condensed’ in the gyromagnetic coupling vector _G_ = −4_πN_Sk_E__z_ and

in the dissipative tensor \(\underline{D}\) with elements \({D}_{ij}=\int {{\rm{\partial }}}_{i}{\boldsymbol{m}}({\boldsymbol{r}})\cdot {{\rm{\partial

}}}_{j}{\boldsymbol{m}}({\boldsymbol{r}})\,{{\rm{d}}}^{2}r\). Only _D__xx_ = _D__yy_ are nonzero. _b_ = _M__s__d__z_/_γ__e_ is determined by the saturation magnetization _M__s_, the disk

thickness _d__z_ and the gyromagnetic ratio of an electron _γ__e_. Due to the disk geometry the force _F_int, that covers interactions of the considered quasiparticle with other

quasiparticles or with the edge of the sample, is radially symmetric. The Thiele equation in polar coordinates $$4\pi {N}_{{\rm{Sk}}}b(r\dot{\varphi

}{{\boldsymbol{e}}}_{r}-\dot{r}{{\boldsymbol{e}}}_{\varphi })-\alpha {D}_{xx}b(\dot{r}{{\boldsymbol{e}}}_{r}+r\dot{\varphi }{{\boldsymbol{e}}}_{\varphi

})+{F}_{{\rm{int}}}(r){{\boldsymbol{e}}}_{r}=0$$ (6) yields $$\begin{array}{rcl}\dot{r} & = & \frac{{F}_{{\rm{int}}}(r)}{{(\alpha {D}_{xx})}^{2}b+{(4\pi {N}_{{\rm{Sk}}})}^{2}b}\alpha

{D}_{xx},\\ \dot{\varphi } & = & \frac{{F}_{{\rm{int}}}(r)}{{(\alpha {D}_{xx})}^{2}b+{(4\pi {N}_{{\rm{Sk}}})}^{2}b}\frac{-4\pi {N}_{{\rm{Sk}}}}{r}.\end{array}$$ (7) Since

_F_int(_r_) < 0, a skyrmion moves to the nanodisk’s center along a counter-clockwise spiral trajectory (\(\dot{r} < 0\), \(\dot{\varphi } > 0\)). When it approaches the center, the

angular velocity decreases since _F_int(_r_) drops faster to 0 than 1/_r_. The transverse component of the spiral motion is a consequence of the skyrmion’s topological charge. Like any

quasiparticle with nontrivial real-space topology a skyrmion does not move parallel to the propelling force — let it be due to a current or the skyrmion–edge interaction3,8,9,31,67,68 — and

thus exhibits a skyrmion Hall effect. The corresponding transverse force is similar to the Magnus force for classical particles3,69. FORMATION OF BISKYRMIONS The formation of a biskyrmion

starts with two Bloch skyrmions with opposite helicities of _γ_ = ±_π_/2, as stabilized in Fig. 3. Since both skyrmions have identical dissipative tensors \(\underline{D}\) and topological

charges _N_Sk = +1, the equations of motion (7) hold for both quasiparticles. They move on a spiral trajectory towards the nanodisk’s center. However, the skyrmion-skyrmion interaction has

to be considered in _F_int. This force changes sign when both skyrmions come close to each other, corresponding to the energy minimum in Fig. 2a; it is zero at a finite distance of the two

skyrmions. This behavior is well visible in the results of micromagnetic simulations (Fig. 5). After the writing period (relaxation after ≈1 ns as presented in Fig. 3), both skyrmions start

to exhibit a spiral motion to the center as in the case of a single skyrmion. Once both skyrmions start to overlap the spiral motion stops and a biskyrmion is formed. During the formation

process the topological charge remains _N_Sk = +2 within an error of less than 1.5% (the topological charge is not integer due to the discreteness of the underlying lattice). The biskyrmion

configuration is remarkably stable. The energy drops significantly once the two skyrmions are close to each other (Fig. 5d). This drop corresponds to the energy minimum established in the

analytic model (Fig. 2a). In the final phase of the propagation the biskyrmion aligns with one of the crystallographic directions _α_ = 45°, 135°, 225° or 315°, visible as energy minimum in

Fig. 2c (here: _α_ = 135°). Once the system is close to the energy minimum _F_int is far from being rotational symmetric and the equations of motion derived from the Thiele equation do not

hold anymore. By comparing the energy scales of Figs. 2a,c it becomes apparent that the reorientation of the biskyrmion plays a role after the optimal distance of the two skyrmions has been

reached. The distinguished axis of the biskyrmion can in principle be imposed by the initial positions of the skyrmions. If the two writing disks are closer together the biskyrmion can end

for example at _α_ = 45° (Fig. S1 of the Supplementary Information). Starting with two skyrmions with _identical_ helicity (i. e. by switching one of the two writing vortices) a mostly

static behavior is observed (Fig. S2 of the Supplementary Information). This is readily explained by the stronger repulsion of skyrmions with the same helicity in comparison to those with

opposite helicities. Due to the disk geometry both skyrmions experience a force towards the center, resulting in a zero of _F_int at larger distances compared to the biskyrmion system. The

(final) steady state — two skyrmions without considerable overlap — has a sizably higher energy than the biskyrmion state (cf. Fig. S2d and Fig. 5d). Starting from this particular

configuration a biskyrmion does not form since one skyrmion would have to reverse its helicity. That, however, requires to overcome an energy barrier similar to that in Fig. 2b,

corresponding to a Néel skyrmion state. In refs.16,17 it was shown that asymmetric skyrmion tubes (e. g. in the cone phase of chiral magnetic materials) can exhibit an attractive interaction

despite their equal helicities. The resulting non-overlapping pair of skyrmions is stabilized by a different mechanism and at a larger inter-skyrmion distance compared to the type of

biskyrmion discussed in the present paper. Nevertheless, the skyrmion-skyrmion pair was labeled ‘biskyrmion’ in ref.16 due to the topological equivalence (_N_Sk = ±2) of both textures. Yet,

both are geometrically distinct objects. DISCUSSION Here, we have demonstrated that the dipole-dipole interaction in centrosymmetric magnetic systems can stabilize _isolated biskyrmions_, in

the sense of a pair of partially overlapping skyrmions with reversed in-plane magnetizations. We propose methods for writing two Bloch skyrmions with opposite helicities at opposite sides

of a nanodisk. After spiral propagation of each skyrmion towards the nanodisk’s center, an _isolated biskyrmion_ is formed due to the attractive interaction that originates in the

dipole-dipole interaction. These ingredients provide a step towards utilizing biskyrmions as carriers of information in spintronics devices. To the best of our knowledge, only biskyrmion

_lattices_ have been found experimentally so far18,19,20,21,22, and even for them the interpretation of the presented Lorentz transmission electron microscopy images is under serious debate.

In two recent publications it was shown that tubes of topologically trivial bubbles (called type-II or hard bubbles) can appear as biskyrmion-like features when observed under an

angle70,71. Since thin magnetic disks are considered in the present work, potential real-space images can hardly be misinterpreted, and therefore our prediction may be decisive for showing

that biskyrmions can exist at all. Besides their potential for applications, biskyrmions are also worth being investigated from a fundamental point of view. Their nontrivial real-space

topology, manifested in the topological charge of _N_Sk = ±2, imposes emergent electrodynamic effects: just like conventional skyrmions, biskyrmions exhibit a skyrmion Hall effect3,8,9,67,68

and a topological Hall effect3,10,11,72,73,74,75,76,77,78. In other words, under the effect of a spin-polarized current the biskyrmion and the current electrons are deflected into

transverse directions. Our study motivates future in-depth analyses of similarities and differences of these Hall effects for skyrmions and biskyrmions. One fundamental aspect that

distinguishes biskyrmions from skyrmions is their missing rotational symmetry. The orientation of a biskyrmion could be exploited to store multiple bits per biskyrmion. Here, the underlying

cubic lattice yields four energetically degenerate orientations _α_ and allows for quaternary instead of binary logic. It is conceivable to store data in an array of nanodisks instead of in

a racetrack device. METHODS For the micromagnetic simulations the Landau-Lifshitz-Gilbert equation48,49,50 $${\dot{{\boldsymbol{m}}}}_{i}=-\,{\gamma }_{e}{{\boldsymbol{m}}}_{i}\times

{{\boldsymbol{B}}}_{i,{\rm{eff}}}+{\alpha }_{g}{{\boldsymbol{m}}}_{i}\times {\dot{{\boldsymbol{m}}}}_{i}+{\gamma }_{e}\varepsilon \beta [({{\boldsymbol{m}}}_{i}\times

{{\boldsymbol{s}}}_{i})\times {{\boldsymbol{m}}}_{i}]$$ (8) is solved using Mumax346,47. The first term describes the precession of each magnetic moment around its instantaneous effective

magnetic field \({{\boldsymbol{B}}}_{{\rm{eff}}}^{i}=-\,{\delta }_{{{\boldsymbol{m}}}_{i}}F/{M}_{s}\). This field, derived from the free energy density _F_, takes into account exchange

interaction, uniaxial anisotropy, Zeeman energy, and the demagnetization field accounting for the dipole-dipole interaction. The second term, introduced phenomenologically, considers that

the magnetic moments tend to align along their effective magnetic field. The strength of this damping is quantified by the Gilbert damping constant _α__g_. The third term accounts for the

coupling of the magnetic moments with injected spin-polarized currents. The in-plane torque coefficient _εβ_ = _ħPj_/2_ed__z__M__s_ depends on the current’s spin polarization _P_ and the

current density _j_. The spatial distribution of the injected spins {_S__i_} is given by the vortex textures in the writing disks. An out-of-plane torque has been neglected since it is

usually small and merely rescales the external magnetic field. _γ__e_ = 1.760 × 1011 T−1s−1 is the gyromagnetic ratio of an electron. We use parameters that stabilize stray-field skyrmions,

similar to those in ref.35: exchange _A_ = 15 pJ/m, uniaxial anisotropy in _z_ direction _K__z_ = 1.2 MJ/m3, external field _B_ = −40 mT_E__z_ (along the ferromagnetic orientation),

saturation magnetization _M__s_ = 1.4 MA/m, and Gilbert damping _α__g_ = 0.3. The disk has a radius of 150 nm and a thickness of _d__z_ = 3 nm. For the simulations we used discrete

magnetization cells of size 1 nm × 1 nm × 1 nm. The DMI has been set to zero. We checked that a small DMI constant (interfacial DMI _D_ = 0.1 mJ/m2) does not qualitatively affect the results

of the simulations shown in Fig. 5; for larger values of _D_ one of the two skyrmions would annihilate and a biskyrmion would not form. As stated in the main text, a spin-polarized current

of  _J_write_P_ = 7 × 108 A/cm−2_E__z_ with a spin polarization orientation {_S__i_}, given by an in-plane vortex texture $${{\boldsymbol{s}}}_{i}=\pm (\,-\,y,x\mp {\rm{\Delta

}}x/2,0)/\sqrt{{({x}_{i}\pm {\rm{\Delta }}x/2)}^{2}+{y}^{2}},$$ (9) writes well-defined skyrmions into the nanodisk, if the current is applied for 200 ps. The two signs correspond to the

left and right writing disks, respectively. The writing disks have a radius of 25 nm each and their centers are at a distance of 120 nm. The writing disks and the process of spin

polarization have not been simulated explicitly but are condensed into the spin-polarization parameter _P_ which scales the necessary applied current density. ACCESSION CODES The code Mumax3

is accessible at https://github.com/mumax/3/releases/tag/v3.9.3. REFERENCES * Bogdanov, A. N. & Yablonskii, D. Thermodynamically stable vortices in magnetically ordered crystals. the

mixed state of magnets. _Zh. Eksp. Teor. Fiz_ 95, 178 (1989). Google Scholar  * Mühlbauer, S. _et al_. Skyrmion lattice in a chiral magnet. _Science_ 323, 915–919,

https://doi.org/10.1126/science.1166767 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. _Nat.

Nanotechnol._ 8, 899–911, https://doi.org/10.1038/nnano.2013.243 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Yu, X. _et al_. Real-space observation of a two-dimensional skyrmion

crystal. _Nature_ 465, 901–904, https://doi.org/10.1038/nature09124 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Parkin, S. S. P. Shiftable magnetic shift register and method of

using the same US Patent 6,834,005 (2004). * Sampaio, J., Cros, V., Rohart, S., Thiaville, A. & Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions

in nanostructures. _Nat. Nanotechnol._ 8, 839, https://doi.org/10.1038/nnano.2013.210 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Romming, N. _et al_. Writing and deleting single

magnetic skyrmions. _Science_ 341, 636–639, https://doi.org/10.1126/science.1240573 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Jiang, W. _et al_. Direct observation of the skyrmion

Hall effect. _Nat. Phys._ 13, 162–169, https://doi.org/10.1038/nphys3883 (2017). Article  CAS  Google Scholar  * Litzius, K. _et al_. Skyrmion Hall effect revealed by direct time-resolved

x-ray microscopy. _Nat. Phys._ 13, 170–175, https://doi.org/10.1038/nphys4000 (2017). Article  CAS  Google Scholar  * Maccariello, D. _et al_. Electrical detection of single magnetic

skyrmions in metallic multilayers at room temperature. _Nat. Nanotechnol_. 13, 233–237 https://doi.org/10.1038/s41565-017-0044-4 (2018). Article  ADS  CAS  PubMed  Google Scholar  *

Hamamoto, K., Ezawa, M. & Nagaosa, N. Purely electrical detection of a skyrmion in constricted geometry. _Appl. Phys. Lett._ 108, 112401, https://doi.org/10.1063/1.4943949 (2016).

Article  ADS  CAS  Google Scholar  * Skyrme, T. H. R. A non-linear field theory. _Proc. Royal Soc. Lond. A: Math. Phys. Eng. Sci._ 260, 127–138 (1961). Article  ADS  MathSciNet  CAS  Google

Scholar  * Biedenharn, L., Sorace, E. & Tarlini, M. Topological concepts in nuclear physics: The deuteron as a bi-skyrmion. In _Symmetries in Science II_, 51–59 (Springer, 1986). *

Schramm, A. J., Dothan, Y. & Biedenharn, L. C. A calculation of the deuteron as a biskyrmion. _Phys. Lett. B_ 205, 151–155, https://doi.org/10.1016/0370-2693(88)91638-3 (1988). Article 

ADS  CAS  Google Scholar  * Hasebe, K. & Ezawa, Z. Grassmannian fields and doubly enhanced skyrmions in the bilayer quantum Hall system at _v_ = 2. _Phys. Rev. B_ 66, 155318,

https://doi.org/10.1103/PhysRevB.66.155318 (2002). Article  ADS  CAS  Google Scholar  * Leonov, A., Monchesky, T., Loudon, J. & Bogdanov, A. Three-dimensional chiral skyrmions with

attractive interparticle interactions. _J. Physics: Condens. Matter_ 28, 35LT01, https://doi.org/10.1088/0953-8984/28/35/35LT01 (2016). Article  CAS  Google Scholar  * Du, H. _et al_.

Interaction of individual skyrmions in a nanostructured cubic chiral magnet. _Phys. Rev. Lett._ 120, 197203, https://doi.org/10.1103/PhysRevLett.120.197203 (2018). Article  ADS  CAS  PubMed

  Google Scholar  * Yu, X. _et al_. Biskyrmion states and their current-driven motion in a layered manganite. _Nat. Commun._ 5, 3198, https://doi.org/10.1038/ncomms4198 (2014). Article  ADS

  CAS  PubMed  Google Scholar  * Wang, W. _et al_. A centrosymmetric hexagonal magnet with superstable biskyrmion magnetic nanodomains in a wide temperature range of 100–340 K. _Adv. Mater._

28, 6887–6893, https://doi.org/10.1002/adma.201600889 (2016). Article  CAS  PubMed  Google Scholar  * Peng, L. _et al_. Real-space observation of nonvolatile zero-field biskyrmion lattice

generation in MnNiGa magnet. _Nano Lett._ 17, 7075–7079, https://doi.org/10.1021/acs.nanolett.7b03792 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Zuo, S. _et al_. Direct observation

of the topological spin configurations mediated by the substitution of rare-earth element y in MnNiGa alloy. _Nanoscale_ 10, 2260–2266, https://doi.org/10.1039/C7NR08997J (2018). Article 

CAS  PubMed  Google Scholar  * Peng, L. _et al_. Multiple tuning of magnetic biskyrmions using _in situ_ L-TEM in centrosymmetric MnNiGa alloy. _J. Physics: Condens. Matter_ 30, 065803,

https://doi.org/10.1088/1361-648X/aaa527 (2018). Article  ADS  Google Scholar  * Zhang, X. _et al_. Skyrmion dynamics in a frustrated ferromagnetic film and current-induced helicity

locking-unlocking transition. _Nat. Commun._ 8, 1717, https://doi.org/10.1038/s41467-017-01785-w (2017). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Okubo, T., Chung, S.

& Kawamura, H. Multiple-q states and the skyrmion lattice of the triangular-lattice heisenberg antiferromagnet under magnetic fields. _Phys. Rev. Lett._ 108, 017206,

https://doi.org/10.1103/PhysRevLett.108.017206 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Leonov, A. & Mostovoy, M. Multiply periodic states and isolated skyrmions in an

anisotropic frustrated magnet. _Nat. Commun._ 6, 8275, https://doi.org/10.1038/ncomms9275 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Göbel, B., Mook, A., Henk, J. & Mertig, I.

Antiferromagnetic skyrmion crystals: Generation, topological Hall, and topological spin Hall effect. _Phys. Rev. B_ 96, 060406(R), https://doi.org/10.1103/PhysRevB.96.060406 (2017). Article

  ADS  Google Scholar  * Malozemoff, A. & Slonczewski, J. _Magnetic Domain Walls in Bubble Materials_ (Academic press, 1979). * Eschenfelder, A. H. _Magnetic bubble technology_

(Springer-Verlag Berlin Heidelberg New York, 1980). * Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. _J.Phys. Chem. Solids_ 4, 241–255,

https://doi.org/10.1016/0022-3697(58)90076-3 (1958). Article  ADS  CAS  Google Scholar  * Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. _Physical Review_ 120, 91,

https://doi.org/10.1103/PhysRev.120.91 (1960). Article  ADS  CAS  Google Scholar  * Göbel, B., Mook, A., Henk, J., Mertig, I. & Tretiakov, O. A. Magnetic bimerons as skyrmion analogues

in in-plane magnets. _Phys. Rev. B_ 99, 060407(R), https://doi.org/10.1103/PhysRevB.99.060407 (2019). Article  ADS  Google Scholar  * Lin, Y., Grundy, P. & Giess, E. Bubble domains in

magnetostatically coupled garnet films. _Appl. Phys. Lett._ 23, 485–487, https://doi.org/10.1063/1.1654968 (1973). Article  ADS  CAS  Google Scholar  * Takao, S. A study of magnetization

distribution of submicron bubbles in sputtered Ho-Co thin films. _J. Magn. Magn. Mater._ 31, 1009–1010, https://doi.org/10.1016/0304-8853(83)90772-2 (1983). Article  ADS  Google Scholar  *

Jiang, W. _et al_. Blowing magnetic skyrmion bubbles. _Science_ 349, 283–286, https://doi.org/10.1126/science.aaa1442 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Büttner, F.,

Lemesh, I. & Beach, G. S. Theory of isolated magnetic skyrmions: From fundamentals to room temperature applications. _Sci. Reports_ 8, 4464, https://doi.org/10.1038/s41598-018-22242-8

(2018). Article  ADS  CAS  Google Scholar  * Aharoni, A. _et al_. _Introduction to the Theory of Ferromagnetism_, vol. 109 (Clarendon Press, 2000). * Derrick, G. Comments on nonlinear wave

equations as models for elementary particles. _J. Math. Phys._ 5, 1252–1254 (1964). Article  ADS  MathSciNet  CAS  Google Scholar  * Rajaraman, R. _Solitons and instantons_ (North Holland,

1987). * Gioia, G. & James, R. D. Micromagnetics of very thin films. _Proc. Royal Soc. London. Ser. A: Math. Phys. Eng. Sci._ 453, 213–223, https://doi.org/10.1098/rspa.1997.0013 (1997).

Article  ADS  CAS  Google Scholar  * Guslienko, K. Y. Skyrmion state stability in magnetic nanodots with perpendicular anisotropy. _IEEE Magn. Lett._ 6, 4000104,

https://doi.org/10.1109/LMAG.2015.2413758 (2015). Article  Google Scholar  * Vidal-Silva, N., Riveros, A. & Escrig, J. Stability of Néel skyrmions in ultra-thin nanodots considering

Dzyaloshinskii-Moriya and dipolar interactions. _J. Magn. Magn. Mater._ 443, 116–123, https://doi.org/10.1016/j.jmmm.2017.07.049 (2017). Article  ADS  CAS  Google Scholar  * Riveros, A.,

Vidal-Silva, N., Tejo, F. & Escrig, J. Analytical and numerical Ku-B phase diagrams for cobalt nanostructures: Stability region for a Bloch skyrmion. _J. Magn. Magn. Mater._ 460,

292–296, https://doi.org/10.1016/j.jmmm.2018.04.018 (2018). Article  ADS  CAS  Google Scholar  * Guslienko, K. Y. Néel skyrmion stability in ultrathin circular magnetic nanodots. _Applied

Physics Express_ 11, 063007, https://doi.org/10.7567/APEX.11.063007 (2018). Article  ADS  Google Scholar  * Tejo, F., Riveros, A., Escrig, J., Guslienko, K. & Chubykalo-Fesenko, O.

Distinct magnetic field dependence of Néel skyrmion sizes in ultrathin nanodots. _Sci. Reports_ 8, 6280, https://doi.org/10.1038/s41598-018-24582-x (2018). Article  ADS  CAS  Google Scholar

  * Castro, M. A. & Allende, S. Skyrmion core size dependence as a function of the perpendicular anisotropy and radius in magnetic nanodots. _J. Magn. Magn. Mater._ 417, 344–348,

https://doi.org/10.1016/j.jmmm.2016.05.095 (2016). Article  ADS  CAS  Google Scholar  * Vansteenkiste, A. & Van de Wiele, B. MuMax: a new high-performance micromagnetic simulation tool.

_J. Magn. Magn. Mater._ 323, 2585–2591, https://doi.org/10.1016/j.jmmm.2011.05.037 (2011). Article  ADS  CAS  Google Scholar  * Vansteenkiste, A. _et al_. The design and verification of

MuMax3. _AIP Adv._ 4, 107133, https://doi.org/10.1063/1.4899186 (2014). Article  ADS  CAS  Google Scholar  * Landau, L. D. & Lifshitz, E. On the theory of the dispersion of magnetic

permeability in ferromagnetic bodies. _Phys. Z. Sowjetunion_ 8, 101–114 (1935). MATH  Google Scholar  * Gilbert, T. L. A phenomenological theory of damping in ferromagnetic materials. _IEEE

Transactions on Magn._ 40, 3443–3449, https://doi.org/10.1109/TMAG.2004.836740 (2004). Article  ADS  CAS  Google Scholar  * Slonczewski, J. C. Current-driven excitation of magnetic

multilayers. _J. Magn. Magn. Mater._ 159, L1–L7, https://doi.org/10.1016/0304-8853(96)00062-5 (1996). Article  ADS  CAS  Google Scholar  * Cowburn, R., Koltsov, D., Adeyeye, A., Welland, M.

& Tricker, D. Single-domain circular nanomagnets. _Phys. Rev. Lett._ 83, 1042, https://doi.org/10.1103/PhysRevLett.83.1042 (1999). Article  ADS  CAS  Google Scholar  * Shinjo, T., Okuno,

T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. _Science_ 289, 930–932, https://doi.org/10.1126/science.289.5481.930 (2000).

Article  ADS  CAS  PubMed  Google Scholar  * Sun, L. _et al_. Creating an artificial two-dimensional skyrmion crystal by nanopatterning. _Phys. Rev. Lett._ 110, 167201,

https://doi.org/10.1103/PhysRevLett.110.167201 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Miao, B. _et al_. Experimental realization of two-dimensional artificial skyrmion crystals

at room temperature. _Phys. Rev. B_ 90, 174411, https://doi.org/10.1103/PhysRevB.90.174411 (2014). Article  ADS  CAS  Google Scholar  * Gilbert, D. A. _et al_. Realization of ground-state

artificial skyrmion lattices at room temperature. _Nat. Commun._ 6, 8462, https://doi.org/10.1038/ncomms9462 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Loreto, R. _et al_.

Creation, transport and detection of imprinted magnetic solitons stabilized by spin-polarized current. _J. Magn. Magn. Mater._ 455, 25–31, https://doi.org/10.1016/j.jmmm.2017.04.074 (2018).

Article  ADS  CAS  Google Scholar  * Taniuchi, T., Oshima, M., Akinaga, H. & Ono, K. Vortex-chirality control in mesoscopic disk magnets observed by photoelectron emission microscopy.

_J. Appl. Phys._ 97, 10J904, https://doi.org/10.1063/1.1862032 (2005). Article  CAS  Google Scholar  * Gaididei, Y., Sheka, D. D. & Mertens, F. G. Controllable switching of vortex

chirality in magnetic nanodisks by a field pulse. _Appl. Phys. Lett._ 92, 012503, https://doi.org/10.1063/1.2829795 (2008). Article  ADS  CAS  Google Scholar  * Konoto, M. _et al_. Formation

and control of magnetic vortex chirality in patterned micromagnet arrays. _J. Appl. Phys._ 103, 023904, https://doi.org/10.1063/1.2828177 (2008). Article  ADS  CAS  Google Scholar  *

Yakata, S., Miyata, M., Nonoguchi, S., Wada, H. & Kimura, T. Control of vortex chirality in regular polygonal nanomagnets using in-plane magnetic field. _Appl. Phys. Lett._ 97, 222503,

https://doi.org/10.1063/1.3521407 (2010). Article  ADS  CAS  Google Scholar  * Bogdanov, A. & Hubert, A. The stability of vortex-like structures in uniaxial ferromagnets. _J. Magn. Magn.

Mater._ 195, 182–192, https://doi.org/10.1016/S0304-8853(98)01038-5 (1999). Article  ADS  CAS  Google Scholar  * Zhang, X. _et al_. Control and manipulation of a magnetic skyrmionium in

nanostructures. _Phys. Rev. B_ 94, 094420, https://doi.org/10.1103/PhysRevB.94.094420 (2016). Article  ADS  CAS  Google Scholar  * Göbel, B., Schäffer, A. F., Berakdar, J., Mertig, I. &

Parkin, S. S. P. Electrical writing, deleting, reading, and moving of magnetic skyrmioniums in a racetrack device. _arXiv preprint:1902.06295_ (2019). * Yang, Y. _et al_. Ultrafast

magnetization reversal by picosecond electrical pulses. _Science Advances_ 3, e1603117, https://doi.org/10.1126/sciadv.1603117 (2017). Article  ADS  CAS  PubMed  PubMed Central  Google

Scholar  * Schäffer, A. F., Dürr, H. A. & Berakdar, J. Ultrafast imprinting of topologically protected magnetic textures via pulsed electrons. _Appl. Phys. Lett._ 111, 032403,

https://doi.org/10.1063/1.4991521 (2017). Article  ADS  CAS  Google Scholar  * Thiele, A. Steady-state motion of magnetic domains. _Phys. Rev. Lett._ 30, 230,

https://doi.org/10.1103/PhysRevLett.30.230 (1973). Article  ADS  Google Scholar  * Göbel, B., Mook, A., Henk, J. & Mertig, I. Overcoming the speed limit in skyrmion racetrack devices by

suppressing the skyrmion Hall effect. _Phys. Rev. B_ 99, 020405(R), https://doi.org/10.1103/PhysRevB.99.020405 (2019). Article  ADS  Google Scholar  * Zang, J., Mostovoy, M., Han, J. H.

& Nagaosa, N. Dynamics of skyrmion crystals in metallic thin films. _Phys. Rev. Lett._ 107, 136804, https://doi.org/10.1103/PhysRevLett.107.136804 (2011). Article  ADS  CAS  PubMed 

Google Scholar  * Everschor-Sitte, K. & Sitte, M. Real-space Berry phases: Skyrmion soccer. _J. Appl. Phys._ 115, 172602, https://doi.org/10.1063/1.4870695 (2014). Article  ADS  CAS 

Google Scholar  * Loudon, J. C. _et al_. Do images of biskyrmions show type-ii bubbles? _Adv. Mater_. 1806598, https://doi.org/10.1002/adma.201806598 (2019). Article  Google Scholar  * Yao,

Y. _et al_. Magnetic hard nanobubble: A possible magnetization structure behind the bi-skyrmion. _Appl. Phys. Lett._ 114, 102404, https://doi.org/10.1063/1.5083971 (2019). Article  ADS  CAS

  Google Scholar  * Bruno, P., Dugaev, V. & Taillefumier, M. Topological Hall effect and Berry phase in magnetic nanostructures. _Phys. Rev. Lett._ 93, 096806,

https://doi.org/10.1103/PhysRevLett.93.096806 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Neubauer, A. _et al_. Topological Hall effect in the A phase of MnSi. _Phys. Rev. Lett._

102, 186602, https://doi.org/10.1103/PhysRevLett.102.186602 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Hamamoto, K., Ezawa, M. & Nagaosa, N. Quantized topological Hall effect

in skyrmion crystal. _Phys. Rev. B_ 92, 115417, https://doi.org/10.1103/PhysRevB.92.115417 (2015). Article  ADS  CAS  Google Scholar  * Göbel, B., Mook, A., Henk, J. & Mertig, I.

Unconventional topological Hall effect in skyrmion crystals caused by the topology of the lattice. _Phys. Rev. B_ 95, 094413, https://doi.org/10.1103/PhysRevB.95.094413 (2017). Article  ADS

  Google Scholar  * Göbel, B., Mook, A., Henk, J. & Mertig, I. Signatures of lattice geometry in quantum and topological Hall effect. _New J. Phys._ 19, 063042,

https://doi.org/10.1088/1367-2630/aa709b (2017). Article  ADS  CAS  Google Scholar  * Göbel, B., Mook, A., Henk, J. & Mertig, I. The family of topological Hall effects for electrons in

skyrmion crystals. _The Eur. Phys. J. B_ 91, 179, https://doi.org/10.1140/epjb/e2018-90090-0 (2018). Article  ADS  MathSciNet  CAS  Google Scholar  * Nakazawa, K., Bibes, M. & Kohno, H.

Topological Hall effect from strong to weak coupling. _J. Phys. Soc. Jpn._ 87, 033705, https://doi.org/10.7566/JPSJ.87.033705 (2018). Article  ADS  Google Scholar  Download references

ACKNOWLEDGEMENTS B.G. is thankful to Alexander F. Schäffer regarding discussions about Mumax and possible alternative writing approaches. This work is supported by Priority Program SPP 1666

and SFB 762 of Deutsche Forschungsgemeinschaft (DFG). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Max-Planck-Institut für Mikrostrukturphysik, Halle (Saale), 06120, Germany Börge Göbel 

& Ingrid Mertig * Martin-Luther-Universität Halle-Wittenberg, Institut für Physik, Halle (Saale), 06099, Germany Jürgen Henk & Ingrid Mertig Authors * Börge Göbel View author

publications You can also search for this author inPubMed Google Scholar * Jürgen Henk View author publications You can also search for this author inPubMed Google Scholar * Ingrid Mertig

View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS B.G. initiated the project and performed the calculations. B.G. wrote the manuscript with

the help of J.H. All authors discussed the results and commented on the manuscript. CORRESPONDING AUTHOR Correspondence to Börge Göbel. ETHICS DECLARATIONS COMPETING INTERESTS The authors

declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY VIDEO 1 SUPPLEMENTARY VIDEO 2 SUPPLEMENTARY VIDEO 3 SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is

licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Göbel, B., Henk, J. & Mertig, I. Forming individual

magnetic biskyrmions by merging two skyrmions in a centrosymmetric nanodisk. _Sci Rep_ 9, 9521 (2019). https://doi.org/10.1038/s41598-019-45965-8 Download citation * Received: 28 February

2019 * Accepted: 17 June 2019 * Published: 02 July 2019 * DOI: https://doi.org/10.1038/s41598-019-45965-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read

this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative