News Reader.info

ABSTRACT Waves with tailored shape and vectorial non-homogeneous polarization are of much interest due to the many prospects for relevant applications in the classical and quantum domains.

Such vector beams can be generated naturally via conical diffraction in optically biaxial crystals. The recent strongly revived attention to this phenomenon is motivated by modern

applications such as optical trapping, polarimetry or super-resolution imaging, partly enabled by new configurations increasing the beam complexity, like those with several crystals in

cascade. However, up to now all beams generated by conical diffraction conserve at their sharpest plane the underlying circular shape connected with the planar section of light cones. Here

we show that a proper manipulation in wave-vector space within a conical diffraction cascade produces vector beams with highly peculiar non-circular forms, leading to an interesting and

reconfigurable platform for easily shaping all structured wave properties, increasing complexity and information content. The experimental observations are confirmed by numerical integration

of a paraxial model incorporating the effects of the wave-vector space manipulation. SIMILAR CONTENT BEING VIEWED BY OTHERS STRUCTURING TOTAL ANGULAR MOMENTUM OF LIGHT ALONG THE PROPAGATION

DIRECTION WITH POLARIZATION-CONTROLLED META-OPTICS Article Open access 29 October 2021 DUAL-FUNCTIONAL METALENSES FOR THE POLARIZATION-CONTROLLED GENERATION OF FOCALIZED VECTOR BEAMS IN THE

TELECOM INFRARED Article Open access 26 June 2023 SHAPING LIGHT IN 3D SPACE BY COUNTER-PROPAGATION Article Open access 09 September 2021 INTRODUCTION The shaping and structuring of light

beams in terms of intensity, phase and polarization distribution is presently attracting wide attention with applications extending from 3D micro-manipulation and imaging, to classical and

quantum communication1,2. Among the most important custom light fields one counts vector beams that possess a spatially varying light polarization across the beam, as well as beam exhibiting

phase singularities and an optical angular momentum (OAM), such as optical vortices. Besides their strong fundamental interest, such tailored light fields are emerging for an increasing

number of applications. These include optical manipulation or tweezing3,4, the exploiting of OAM for mode division multiplexing in optical communication5 or for quantum information6,7,

super-resolution imaging8, as well as other key enabling technologies in fields including metrology, optical machining, biomedicine, chemistry, and several others1,9. Internal conical

diffraction (CD, also called internal conical refraction) is a natural phenomenon leading to vector beams of circular shape possessing a fractional OAM. This peculiar effect has intrigued

the scientific community since its prediction by W. R. Hamilton nearly 200 years ago and the first experimental observation by H. Lloyd soon after. The CD phenomenon is observed when a

sufficiently tightly focused beam is incident on an optically biaxial crystal (BC) with its wave-vector \(\mathbf {k}\) parallel to one of the optical axes of the crystal10. For this

singular \(\mathbf {k}\)-direction, the Poynting vector directions are degenerate and lie on the surface of a slanted cone with circular base inside the crystal. The section of this cone can

be easily visualized in the plane of tighter focusing of the incident wave (focal image plane, FIP), where one observes two closely spaced circularly shaped bright rings (double rings)

separated by a dark ring (called Poggendorff ring). Two diametrically opposite points always possess orthogonal linear polarizations, leading to the vector beam character10,11,12. An elegant

geometrical explanation on how the Poynting vector directions on the cone depend on the local electric (\(\mathbf {E}\)) and electric displacement vectors (\(\mathbf {D}\)) of the wave is

given in Born and Wolf’s book13. In the last two decades research on CD has been strongly relaunched. This is due on one hand to an improved theoretical understanding of the phenomenon

following its paraxial diffraction theory11 and on the other hand to its potential for several modern photonics applications in the framework of structured light10 among which one may cite

optical trapping14,15, beam shaping16,17, free-space multiplexing for communication18, polarimetry19,20,21, super-resolution imaging22 or OAM management23,24,25. A major recent development

in the field of CD consists in the study of cascaded configurations, where two or more crystals are put in series with their optical axes being aligned26,27,28,29. Such a cascaded CD leads

to a multiplication of the number of observed rings in the FIP, for _N_ crystals one gets \(2^{N-1}\) double rings26. The cascade still has as free parameters the relative rotation angles

\(\gamma _n\) (around the common optical axis) of the _n_th crystal with respect to the first in the cascade. For instance, for \(N=2\) the relative intensities in the two double rings

depend on this angle29, for \(\gamma _2=0\) (parallel crystals) only the external of the two double rings survives, while for \(\gamma _2=\pi\) (antiparallel crystals) only the internal one

survives. For a single crystal the radius of the CD double ring corresponds to the product \(\mathcal {R}=\alpha L\) of the half-angle of aperture \(\alpha\) of the CD cone (depending on the

material birefringence) and the crystal length _L_. Importantly, for two BC in cascade of the same kind (same \(\alpha\)) of lengths \(L_1\) and \(L_2\) the external and internal double

rings have a radius \(\mathcal {R}_{ext} \propto L_1+L_2\) and \(\mathcal {R}_{int} \propto |L_1-L_2|\), respectively26,29. Obviously, if the lengths of the two crystals are identical, the

internal double-ring will degenerate into a central spot. There is however an elegant way introduced recently by Peet30 to modify these radii by a technique called variable two-crystals

cascade. A spherical lens is intercalated between the two cascaded crystals in such a way as to image the FIP near the first crystal into a second FIP near the second BC. It was shown that

the magnification factor _M_ of this imaging modifies the relative values of the observed double ring radii according to \(\mathcal {R}_{ext} \propto M L_1+L_2\) and \(\mathcal {R}_{int}

\propto |M L_1-L_2|\)30. This make the effect much more versatile and allows the continuous tuning of the actual cascade parameters despite using crystals of fixed lengths. With respect to

the intensity distribution, if the input wave has circular polarization the intensity along the rings is homogeneous. An inhomogeneous azimuthal distribution can be achieved by linearly

polarizing the light at the input or output10 or, more drastically, by scrambling the polarization between two or more BCs in cascade17, in which case also polarization patterns of increased

complexity are obtained. Nevertheless, despite for all the above described developments, the CD patterns obtained so far always possess an intrinsic circular shape. This form is associated

to the section of the CD cone with a plane perpendicular to the central light wavevector and the optical axis of the BCs. In this work we show that the circular symmetry can be dramatically

broken by a proper manipulation in the wave-vector space between the BCs in a cascade. This leads to CD patterns with highly increased complexity, both in terms of the shapes and of the

polarization distribution. The resulting vector beams can be modified in an extremely versatile way by changing the positions of the elements inserted in the cascade that will be described

below. Our unexpected experimental observations are shown to be in very good agreement with the predictions of a Fourier domain theoretical model based on paraxial diffraction theory that

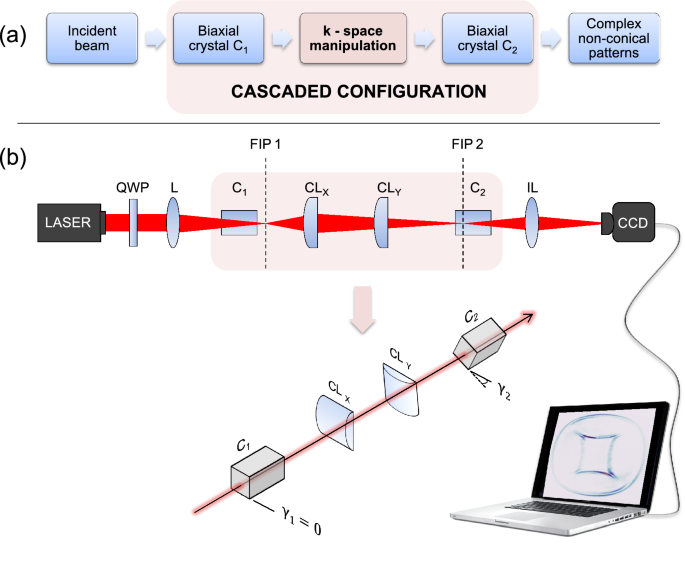
takes into account the applied wave-vector manipulation. PRINCIPLE, OPTICAL SET-UP AND MODELING The concept underlying our approach is illustrated in Fig. 1a. The key aspect is in the

manipulation of the transverse wave-vector space (_k_-space) that effectively splits this 2D space into two 1D spaces. As seen in the experimental set-up of Fig. 1b, this manipulation is

done with the help of two crossed cylindrical lenses CL\(_x\) and CL\(_y\). The linear polarized He–Ne laser beam (wavelength \(\lambda =633\) nm) is transformed to circular polarization by

the quarter-wave plate (QWP) and focused by the spherical lens L (focal length \(f = 200\) mm) to the first BC (C\(_1\)). The CD in this crystal can be observed as a sharp round and

azimuthally homogeneous double ring at the first focal image plane (FIP1). Importantly, both cylindrical lenses (CL) image this plane into a same plane (the second focal image FIP2) near the

position of the second BC (C\(_2\)), however with different magnification factors \(M_x\) and \(M_y\), respectively. The choice of identical focal lengths for the two CL would leave only

limited versatility for the selection of the \(M_x\) and \(M_y\) values and it is better to choose different focal lengths, in our case \(f_x = 100\) mm for CL\(_x\) and \(f_y = 75\) mm for

CL\(_y\). The cascaded CD pattern is formed in FIP2 and is imaged by the imaging spherical lens IL (\(f = 100\) mm) on the CCD camera. In our experiments KGd(WO4)2 is chosen for both BCs

with lengths \(L_1=22.6\) mm for C\(_1\) and \(L_2=17.6\) mm for C\(_2\). The angles \(\gamma _1\) (chosen = 0) and \(\gamma _2\) give the relative orientation of the two BCs around the

common optical axis, as shown in Fig. 1b. Before discussing the experimental results, we present briefly the main features of the theoretical model utilized to numerically calculate the

expected cascaded CD patterns. The model builds on Berry’s paraxial theory for cascaded CD26 by including the effects of the _k_-space manipulation. It is useful to use normalized

coordinates in both real and wave-vector space so that the polar coordinate radius _r_ in real space becomes \(\rho \equiv r/w\), and the small transverse wave-vector \(k_t\) in _k_-space

(with respect to the exact optical axis direction) becomes \(\kappa \equiv k_t w\), with _w_ being the 1/e intensity width of the input wave at its focal point17,26. We consider an incident

paraxial wave field, whose Fourier transform of the electric displacement vector at the position of FIP1 is \(\mathbf {D}_0(\kappa , \phi )\) with \(\phi\) being the azimuthal angle in polar

coordinates. The distribution of the \(\mathbf {D}\)-field in real space after going through the whole cascade is obtained as $$\begin{aligned} \mathbf {D}(\rho , \varphi ) = \frac{1}{2\pi

} \ \int _{0}^{2\pi } \int _{0}^\infty e^{\iota \kappa \rho \cos (\phi - \varphi )} \mathbf{U _{\hbox {tot}}}\mathbf {D}_0(\kappa , \phi ) \kappa \ d\kappa \ d\phi , \end{aligned}$$ (1)

where \(\varphi\) is the azimuthal angle in real space. Note that here the above real space \(\mathbf {D}\)-field is calculated at the plane FIP1 at which the input field \(\mathbf {D}_0\)

and the width _w_ are defined. It corresponds to the field at FIP2 back imaged to the plane FIP1 by the CL pair. Therefore a forward imaging of this field to plane FIP2 must be performed in

order to compare with the experimental images obtained at the CCD camera. The key element in the above integral is the transfer matrix \(\mathbf{U _{\hbox {tot}}}\) that contains the effect

of the cascade on each plane wave component composing the input beam, i.e. the effects of the two BCs and of all the optical elements in the path. For our situation this transfer function

can be expressed as $$\begin{aligned} \mathbf{U _{\hbox {tot}}}(\kappa , \phi ) = \mathbf{U _{2}}(\kappa ' , \phi ' , \rho _2,\gamma _2) \cdot \ \mathbf{U _{1}}(\kappa , \phi ,

\rho _1, \gamma _1), \end{aligned}$$ (2) where the matrices \(\mathbf{U} _i\) (_i_ = 1, 2) are given as $$\begin{aligned} \mathbf{U} _i(\kappa , \phi , \rho _i, \gamma _i) = \exp \left(

-\iota \kappa \rho _i \begin{bmatrix} \cos (\phi - \gamma _i) &{} \sin (\phi - \gamma _i) \\ \sin (\phi - \gamma _i) &{} -\cos (\phi - \gamma _i) \end{bmatrix}\right) ,

\end{aligned}$$ (3) with \(\rho _i \equiv \alpha L_i / w\) being the normalized strength parameters for the CD in the two crystals, proportional to their lengths \(L_i\). The essential

element in Eq. (2) is the transformation in the wave-vector space coordinates from \((\kappa , \phi )\) to \((\kappa ', \phi ')\) between the two transfer matrices U\(_1\) and

U\(_2\), which reflects the applied _k_-space manipulation. It can be easily shown that the needed transformations are $$\begin{aligned} \kappa ' = \kappa \sqrt{\frac{\cos ^2 \phi

}{M_x^2}+\frac{\sin ^2 \phi }{M_y^2}} \end{aligned}$$ (4) and $$\begin{aligned} \phi ' = \arctan \left[ \frac{M_x}{M_y} \left( \frac{-\sin \phi }{-\cos \phi } \right) \right] .

\end{aligned}$$ (5) In the latter case one needs to take care of the correct quadrant for the arctangent function in accordance with the signs of numerator and denominator inside the round

brackets. The calculations that will be shown below for the two-crystal cascade case are obtained by numerical integration of Eqs. (1) and (2) with an input electric displacement field

\(\mathbf {D}_0=1/\sqrt{2} \exp (-\kappa ^2/2)(1,i)^T\) corresponding to a circularly polarized gaussian beam. The used strength parameters \(\rho _1=17.9\) and \(\rho _2=13.9\) reflect the

experimental focusing conditions and the crystal lengths. The obtained real space complex output field \(\mathbf {D}\) is forward imaged to the plane FIP2 and its local relative intensity is

calculated by its square module (\(I \propto |\mathbf {D}|^2\)). RESULTS AND DISCUSSION We consider first the case where the two BCs are either parallel (\(\gamma _1=\gamma _2=0\)) or

antiparallel (\(\gamma _2=\pi\)), the results are shown in the first two columns of Fig. 2 for magnifications \(M_x=1.25\) and \(M_y=0.325\). Figure 2a (experiments) and b (theory) show the

parallel case. Clearly the pattern is dominated by an internal structure of strongly non-circular shape looking rather like a rotated diamonds symbol in playing cards. This structure has a

reversed curvature, it is convex rather than concave if looked from inside. A very faint external structure can also be recognized both in experiments and theory. For the antiparallel case

(Fig. 2c,d) the situation is reversed. Here the external structure dominates with only spurious presence of the internal one. This oval external structure is always concave and importantly,

cannot be described by the equation of an ellipse, which would be expected by the deformed imaging of a circle with our optical system. Moving radially, both internal and external structures

present two intensity maxima separated by a Poggendorff-like zero-intensity region. In conventional and cascaded CD without _k_-space manipulation, the external of each double ring is the

most intense. This remains true for the oval outer structure with the stronger features on the outside. However, the internal convex structure presents the most intense features on the

inside, which is again an opposite behavior. Obviously in our case the internal structure takes the role of the internal double ring in normal cascaded CD and the external the one of the

external double ring. However, besides for the form, two other major differences exist. The first is that for normal cascaded CD only the external double ring is present for the parallel

case and vice versa, which is exactly contrary to the present situation. The reason is the switch of the transverse wave-vector components signs at the CLs. The second difference is the fact

that in the present case, unlike for normal cascaded CD, the second structure, though very faint, does not vanish completely. This is due to the fact that the destructive interference

leading to this disappearance is not fully complete for our anisotropic imaging case. We can also notice that the light polarization on the pattern is always linear but has a complex

distribution (see red arrows in theoretical pictures). Any two points connected by a central inversion possess orthogonal polarizations. We also note that, unlike in the case where the

patterns would be circular, the intensity distribution within the pattern is highly inhomogeneous. Nevertheless, a symmetry with respect to a horizontal and a vertical axis through the

center is present throughout for the cases of Fig. 2a–d. However, this symmetry is lost when the second BC is no longer parallel or antiparallel to the first one, as seen in Fig. 2e,f, where

\(\gamma _2=\pi /2\). Clearly both structures become roughly equally important and the maximum of intensities are shifted towards one of the diagonals. We attribute this shift to the

artificial chirality introduced into the system by the rotation of the second BC. A comparison of the local polarizations in Fig. 2b,d,f shows the crucial role of the angle \(\gamma _2\) on

the polarizations. The shapes of the CD structures can be easily modified by changing the _k_-space manipulation between the BCs and some examples are given in Fig. 3. The first column (Fig.

 3a,b) displays a situation more strongly stretched in _x_-direction (larger \(M_x\) and smaller \(M_y\)). Here the internal and external structures basically merge to give an upper region

with essentially vertical polarization and a lower one with nearly horizontal polarization, the two being joint by two weak “rings” with polarizations near \(\pm 45^\circ\). The central

column (Fig. 3c,d) corresponds to a case where the anisotropic imaging squeezes both directions. Here the pattern is more gentle and all structures are concave, as is the case (not shown) of

a stretching in both directions. The light distribution is still strongly inhomogeneous and the lack of symmetry with respect to the horizontal and vertical axes are less evident, but still

present. In our calculations (bottom rows of Figs. 2 and 3) the _x_ and _y_ axes are scaled as \(x=-M_x \rho \cos \varphi\) and \(y=-M_y \rho \sin \varphi\), what takes into account the

imaging between the calculated pattern at FIP1 and the observed one at FIP2. The positions of the points of intersection of the obtained structures with these axes merit a discussion. Let’s

call \(\pm X_{\pm }\) and \(\pm Y_{\pm }\) the four intersections of the external (subscript +) and internal structure (subscript −) with the _x_-axis and the _y_-axis, respectively. It can

be easily verified that these intersection points satisfy well the relations $$\begin{aligned} X_{\pm }=M_x \rho _1 \pm \rho _2; \; Y_{\pm }=M_y \rho _1 \pm \rho _2. \end{aligned}$$ (6) For

instance for the case in Fig. 2 these expressions give \(X_+ = 36.3\), \(X_- = 8.5\), \(Y_+ = 19.7\) and \(Y_- = -8.1\) in accordance with the numerical calculations. Similarly, for the case

of Fig. 3c,d one has \(X_+ = 21.1\), \(X_- = -6.0\), \(Y_+ = 18.1\) and \(Y_- = -9.7\). In general the most striking patterns are obtained when either \(X_-\) or \(Y_-\) is negative, but

not both. It is worth noting that the above expressions (6) for \(X_{\pm }\) and \(Y_{\pm }\) are a generalization of the one given by Peet30 for the radii of the double rings in variable

two-crystal cascade by intercalation of a spherical lens. Unfortunately our formulas hold only for the intersection points on the main axes and such simple expressions cannot be given for

points lying obliquely on the structures. Following the above argumentation it is interesting to investigate the case where either \(X_-=0\) or \(Y_-=0\), but not both. This is a partially

1D degenerate situation (degeneration only along one of the two axes) and is a unique feature possible with our _k_-space manipulation that treats the two 1D transverse spaces separately.

The 1D degeneration is obtained if \(M_x F=1\) or \(M_y F=1\), with the factor _F_ defined as \(F \equiv \rho _1/ \rho _2\). In our experiments \(F=L_1/L_2 = 1.284\) and a corresponding 1D

degenerated case (along _x_) is shown in Fig. 3e,f. The obtained CD pattern is composed of an external oval and of a complex internal structure resembling a calligraphic letter \({\mathcal

{I}}\). Unlike for the other patterns in Fig. 3 that exhibit always linear polarization everywhere, here in the very center of the internal structure components of different polarizations

and phases collide and interfere, leading locally to a significant degree of ellipticity. However, away from the degenerate zone the local polarization is still linear also in this exemple.

The technique is obviously not limited to the case of two crystals specifically discussed above and the cascade can be extended to _N_ crystals with intermediate manipulations in _k_-space.

Similar to the case of a conventional _N_-crystals cascade, CD patterns formed by a total of \(2^{N-1}\) structures can be expected in this case. Two calculated examples for the case of a

cascade of three mutually crossed crystals with wave-vector space manipulation between each pair of them are shown in Fig. 4. The simulations are performed using Eq. (1) and the proper

generalization of Eqs. (2), (4) and (5). Here the CD strength parameters of the three BCs are chosen to be \(\rho _1=12.0\), \(\rho _2=9.3\) and \(\rho _3=7.3\) with nearly equal ratios

\(F_{12} \approx F_{23}\) with \(F_{ij} \equiv \rho _i/ \rho _j\). A set of two crossed cylindrical lenses is assumed to be placed between each pair of BCs giving magnifications \(M_{x1}\)

and \(M_{y1}\) between the focal image planes FIP1 and FIP2 (near the first and second crystal), and magnifications \(M_{x2}\) and \(M_{y2}\) between FIP2 and a third focal image plane FIP3

near the last crystal in the cascade. The calculated intensity images depicted on Fig. 4 are those observable at FIP3. The case of Fig. 4a showing four structures looking like orbits with

two of them intersecting each other is obtained for \(M_{x1}=2.50\), \(M_{y1}=4.30\) and \(M_{x2}=1.25\), \(M_{y2}=0.325\). Remarkably, the mere permutation of the \(M_{x1}\) and \(M_{y1}\)

values with the \(M_{x2}\) and \(M_{y2}\) ones leads to a completely different beam shape. This situation is shown in Fig. 4b, where one observes an internal Maltese cross-like shape formed

by the two intersecting convex internal structures, combined with two concave external ones. The above permutation of the magnification values corresponds in practice to exchanging the

cylindrical lenses between the first and second BC with those between the second and the third. The fact that this operation leads to fully different patterns is related to the lack of

commutation of the matrices within the integral (1) associated to a generalization of Eq. (2). Similarly to the relationships (6), the eight intersection points \(\pm X_{\pm \pm }\) and

\(\pm Y_{\pm \pm }\) of the four structures with the _x_- and _y_-axes are found here by $$\begin{aligned} X_{\pm \pm } = M_{x2}(M_{x1} \rho _1 \pm \rho _2) \pm \rho _3 \end{aligned}$$ (7)

and $$\begin{aligned} Y_{\pm \pm } = M_{y2}(M_{y1} \rho _1 \pm \rho _2) \pm \rho _3. \end{aligned}$$ (8) The generalization of these expressions to a longer cascade of _N_ crystals is

straightforward. As it can be easily verified, it is worth noting that the ordering and the signs of the eight values \(X_{++}\), \(X_{+-}\), \(X_{-+}\), \(X_{--}\), \(Y_{++}\), \(Y_{+-}\),

\(Y_{-+}\) and \(Y_{--}\) give a direct qualitative guidance on the kind of structure that can be expected for a given set of parameters. CONCLUSION We have shown that a proper wave-vector

space manipulation within a CD cascade leads to highly structured vector beams with striking non-circular shapes. Our experiments performed with a cascade of two biaxial crystals agree very

well with the predictions of a corresponding paraxial diffraction model. The generalization to a longer cascade is straightforward and leads to a further increase in the CD pattern

complexity. It is also worth mentioning that the addition of intermediate polarization scrambling by electro-optic elements can lead to a switching of the sub-structures in a way similar to

the one proposed in an earlier work17, with speeds potentially of the order of GHz. The fast commutation of such highly complex structures is therefore feasible, which may be used also to

address resonant phenomena, for instance in connection with optical trapping. Furthermore, the structured beams obtained by the technique described here may lead to multi-chamber and

dynamically reconfigurable bottle beams, as an extension to the single chamber bottle beams already demonstrated earlier with CD31. Therefore, we believe that the richness and complexity of

these naturally created vector beams and the versatility to tailor their properties by just a few parameters allows for a new platform for fundamental and applied studies of structured

light. Finally, it is worth mentioning that CD beams present generally very interesting features in terms of the OAM of light23,24,32. As cylindrical lenses are known to modify the OAM, we

expect the present technique to highly enrich the opportunities for its tailoring and its manipulation. DATA AVAILABILITY The datasets generated and/or analysed during the current study are

available from the corresponding author on reasonable request. REFERENCES * Rubinsztein-Dunlop, H. _et al._ Roadmap on structured light. _J. Opt._ 19, 013001 (2016). Article  ADS  Google

Scholar  * Shen, Y., Yang, X., Naidoo, D., Fu, X. & Forbes, A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. _Optica_ 7, 820–831 (2020). Article 

ADS  CAS  Google Scholar  * Dholakia, K. & Čižmár, T. Shaping the future of manipulation. _Nat. Photonics_ 5, 335–342 (2011). Article  ADS  CAS  Google Scholar  * Taylor, M. A., Waleed,

M., Stilgoe, A. B., Rubinsztein-Dunlop, H. & Bowen, W. P. Enhanced optical trapping via structured scattering. _Nat. Photonics_ 9, 669–673 (2015). Article  ADS  CAS  Google Scholar  *

Bozinovic, N. _et al._ Terabit-scale orbital angular momentum mode division multiplexing in fibers. _Science_ 340, 1545–1548 (2013). Article  ADS  CAS  Google Scholar  * Mair, A., Vaziri,

A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. _Nature_ 412, 313–316 (2001). Article  ADS  CAS  Google Scholar  * Molina-Terriza, G.,

Torres, J. P. & Torner, L. Twisted photons. _Nat. Phys._ 3, 305–310 (2007). Article  CAS  Google Scholar  * Maurer, P. _et al._ Far-field optical imaging and manipulation of individual

spins with nanoscale resolution. _Nat. Phys._ 6, 912–918 (2010). Article  CAS  Google Scholar  * Shen, Y. _et al._ Optical vortices 30 years on: OAM manipulation from topological charge to

multiple singularities. _Light Sci. Appl._ 8, 90 (2019). Article  ADS  Google Scholar  * Turpin, A., Loiko, Y. V., Kalkandjiev, T. K. & Mompart, J. Conical refraction: Fundamentals and

applications. _Laser Photonics Rev._ 10, 750–771 (2016). Article  ADS  Google Scholar  * Berry, M. V. Conical diffraction asymptotics: Fine structure of Poggendorff rings and axial spike.

_J. Opt. A Pure Appl. Opt._ 6, 289–300 (2004). Article  ADS  Google Scholar  * Berry, M. V., Jeffrey, M. R. & Lunney, J. G. Conical diffraction: Observations and theory. _Proc. R. Soc. A

Math. Phys. Eng. Sci._ 462, 1629–1642 (2006). ADS  MathSciNet  CAS  MATH  Google Scholar  * Born, M. & Wolf, E. _Principles of Optics_, chap. XV—Optics of crystals, 60th Anniversary

Edition, 7th ed. (Cambridge University Press, 2019). * O’Dwyer, D. P., Ballantine, K. E., Phelan, C. F., Lunney, J. G. & Donegan, J. F. Optical trapping using cascade conical refraction

of light. _Opt. Express_ 20, 21119–21125 (2012). Article  ADS  Google Scholar  * Turpin, A. _et al._ Blue-detuned optical ring trap for Bose–Einstein condensates based on conical refraction.

_Opt. Express_ 23, 1638–1650 (2015). Article  ADS  CAS  Google Scholar  * Peet, V. Biaxial crystal as a versatile mode converter. _J. Opt._ 12, 095706 (2010). Article  ADS  Google Scholar 

* Mohammadou, S., Mohamadou, B. & Montemezzani, G. Complex beam shaping by cascaded conical diffraction with intercalated polarization transforming elements. _Opt. Express_ 25,

25392–25406 (2017). Article  ADS  CAS  Google Scholar  * Turpin, A., Loiko, Y., Kalkandjiev, T. K. & Mompart, J. Free-space optical polarization demultiplexing and multiplexing by means

of conical refraction. _Opt. Lett._ 37, 4197–4199 (2012). Article  ADS  CAS  Google Scholar  * Sun, X. _et al._ Unitary transformation for poincaré beams on different parts of poincaré

sphere. _Sci. Rep._ 10, 1–10 (2020). ADS  CAS  Google Scholar  * Novikova, T. _et al._ Metrology of replicated diffractive optics with Mueller polarimetry in conical diffraction. _Opt.

Express_ 15, 2033–2046 (2007). Article  ADS  Google Scholar  * Peinado, A. _et al._ Optimization, tolerance analysis and implementation of a Stokes polarimeter based on the conical

refraction phenomenon. _Opt. Express_ 23, 5636–5652 (2015). Article  ADS  CAS  Google Scholar  * Caron, J. _et al._ Conical diffraction illumination opens the way for low phototoxicity

super-resolution imaging. _Cell Adhes. Migr._ 8, 430–439 (2014). Article  MathSciNet  Google Scholar  * O’Dwyer, D. P. _et al._ Generation of continuously tunable fractional optical orbital

angular momentum using internal conical diffraction. _Opt. Express_ 18, 16480–16485 (2010). Article  ADS  Google Scholar  * Brenier, A. Evolution of vortices created by conical diffraction

in biaxial crystals versus orbital angular momentum. _Opt. Mater._ 110, 110504 (2020). Article  CAS  Google Scholar  * Turpin, A., Rego, L., Picón, A., San Román, J. & Hernández-García,

C. Extreme ultraviolet fractional orbital angular momentum beams from high harmonic generation. _Sci. Rep._ 7, 1–10 (2017). Article  Google Scholar  * Berry, M. V. Conical diffraction from

an N-crystal cascade. _J. Opt._ 12, 075704 (2010). Article  ADS  Google Scholar  * Phelan, C. F., Ballantine, K. E., Eastham, P. R., Donegan, J. F. & Lunney, J. G. Conical diffraction of

a Gaussian beam with a two crystal cascade. _Opt. Express_ 20, 13201–13207 (2012). Article  ADS  CAS  Google Scholar  * Grant, S. D. & Abdolvand, A. Left- and right-circularly polarized

light in cascade conical diffraction. _Opt. Lett._ 37, 5226–5228 (2012). Article  ADS  CAS  Google Scholar  * Turpin, A., Loiko, Y. V., Kalkandjiev, T. K. & Mompart, J. Multiple rings

formation in cascaded conical refraction. _Opt. Lett._ 38, 1455–1457 (2013). Article  ADS  Google Scholar  * Peet, V. Variable two-crystal cascade for conical refraction. _Opt. Lett._ 40,

2405–2408 (2015). Article  ADS  CAS  Google Scholar  * Turpin, A. _et al._ Optical vault: A reconfigurable bottle beam based on conical refraction of light. _Opt. Express_ 21, 26335–26340

(2013). Article  ADS  CAS  Google Scholar  * Brenier, A., Majchrowski, A. & Michalski, E. Light propagation properties of the Bi\(_2\)ZnOB\(_2\)O\(_6\) acentric biaxial crystal: Angular

orbital momentum from conical diffraction. _Opt. Mater._ 91, 286–291 (2019). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This research work was funded by the

Lorraine Université d’Excellence (LUE) initiative. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Université de Lorraine, CentraleSupélec, LMOPS, 57000, Metz, France Muhammad Waqar Iqbal, 

Nicolas Marsal & Germano Montemezzani * Chair in Photonics, CentraleSupélec, LMOPS, 57000, Metz, France Muhammad Waqar Iqbal, Nicolas Marsal & Germano Montemezzani Authors * Muhammad

Waqar Iqbal View author publications You can also search for this author inPubMed Google Scholar * Nicolas Marsal View author publications You can also search for this author inPubMed 

Google Scholar * Germano Montemezzani View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS The concept, experiments and theoretical model were

conceived by all the authors. M.W.I. performed the experiments and the numerical calculations. All authors analysed the results and wrote and reviewed the manuscript. CORRESPONDING AUTHOR

Correspondence to Muhammad Waqar Iqbal. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature

remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the

article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your

intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence,

visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Iqbal, M.W., Marsal, N. & Montemezzani, G. Non-circularly shaped conical

diffraction. _Sci Rep_ 12, 7317 (2022). https://doi.org/10.1038/s41598-022-10749-0 Download citation * Received: 05 February 2022 * Accepted: 07 April 2022 * Published: 05 May 2022 * DOI:

https://doi.org/10.1038/s41598-022-10749-0 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative