News Reader.info

ABSTRACT Orbitally shaking bioreactors (OSRs) have recently been increasingly applied in the biopharmaceutical industry because they can provide a suitable environment for mammalian cell

growth and protein expression. Fluid dynamics information is crucial for analyzing or optimizing of different types of bioreactors. Considering that the structure has an important influence

on the fluid dynamics in a bioreactor, it necessary to design or optimize its structure by the computational fluid dynamics (CFD) approach. The aim of this study is to optimize the wall

structure of a hollow cylinder OSR proposed in our previous work. Based on previous research, the influences of the hollow wall of the OSR on fluid dynamics and the volumetric mass transfer

coefficient (\(k_{L}a\)) were analysed by the established CFD model. The results showed that the mixing performance of OSR could be improved by decreasing the installation height of the

hollow wall. An installation height of 30 mm was found to be most favourable for mixing. The reliability of the CFD model was verified by comparing the liquid wave height and liquid wave

shape between the simulation and experiment. The shear stress in the hollow cylinder OSR was proven gentle for mammalian cell cultivation. SIMILAR CONTENT BEING VIEWED BY OTHERS VALIDATION

OF COMPUTATIONAL FLUID DYNAMICS OF SHAKE FLASK EXPERIMENTS AT MODERATE VISCOSITY BY LIQUID DISTRIBUTIONS AND VOLUMETRIC POWER INPUTS Article Open access 13 February 2024 CHARACTERIZING THE

EFFECT OF IMPELLER DESIGN IN PLANT CELL FERMENTATIONS USING CFD MODELING Article Open access 18 March 2025 CFD SIMULATION OF IMPELLER SHAPE EFFECT ON THE SOLID CLOUD VOLUME IN THE SOLID AND

LIQUID STIRRED VESSEL Article Open access 24 February 2025 INTRODUCTION Bioreactors are critical equipment used for mammalian cell culture. Currently, stirred tank bioreactors (STRs) and

orbital shaken bioreactors (OSRs) are common types of bioreactors widely used in either laboratory or pilot-scale mammalian cell cultivations1,2,3. In recent years, OSRs have become

increasingly popular because of their simple stirring principle, low cost, simple operation and suitability for disposable experiments4,5. Moreover, the orbital shaking motion of OSRs could

prevents sedimentation and enhance gas exchange, avoiding the damagingly high shear rates relative to STRs6. As an important disposable bioreactor, improving the mixing performance of OSRs

is necessary. Research has shown that different structures of OSRs have different effects on mixing performance7,8. For example, introducing a vertical baffle on a wall is an effective way

to improve turbulence characteristics and mixing performance9. A helical track was proven valid for increasing viable cell density in suspension cultivation10. A vaulted “bump” was proposed

on the bottom wall, and the result showed that the mass transfer rate was enhanced significantly and that cell accumulation near the centre of the bottom wall could be avoided, which is

preferable for suspension cultivation with a high viable cell density11. Computational fluid dynamics (CFD) simulation is a reliable numerical analysis technology12,13. Compared to

traditional experimental techniques, CFD simulation can save capital and labour and be used in many different situations14,15. Considering that it can provide a deeper understanding of

bioreactor fluid dynamics and reduce the number of models, CFD simulation has been seen as a valuable tool for analysing bioreactors, such as STRs and OSRs16,17,18. In a previous study19, we

proposed a new type of OSR with a hollow cylindrical wall. For this kind of OSR, the ratio of the outer cylinder diameter to the intercylinder diameter is the key structural parameter. In

that prototype study, the value d\(_{i}\)/d was optimized, and a suitable value of 0.4 was suggested18. However, the mass transfer capability was still low in some specific regions, which

strongly indicated that the structure of the hollow cylindrical wall could be further optimized. Thus, the aim of this study is to continue focusing on the OSR with a hollow cylindrical wall

and analysing the effect of the installation height of the hollow structure on the mixing performance, volumetric mass transfer coefficient (\(k_{L}a\)) and shear stress in the OSR by the

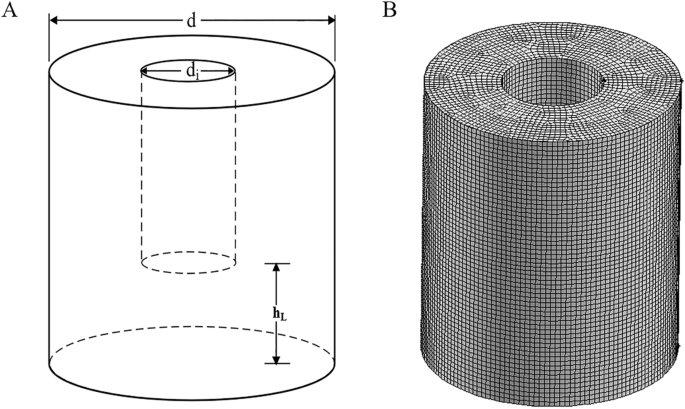
CFD method. MATERIALS AND METHODS BIOREACTOR The OSR with a hollow cylindrical wall was orbitally shaken on an ES-X shaker (Kühner AG, Biersfelden, Switzerland) with a shaking diameter of 50

mm. In this study, the total volume of the hollow cylindrical OSRs was approximately 24 L, the height of the vessel was 0.35 m, the outer diameter (d) was 0.3 m, and the inner diameter

(d\(_{i}\)) was 0.12 m. All experiments and simulations in this paper were carried out under the conditions of a filling volume of 8 L and shaking speed of 100 rpm. The installation height

of the intercylinder wall from the bottom was represented by h\(_{\mathrm {L}}\) (see Fig. 1). LIQUID WAVE CAPTURING The moving gas-liquid interface was captured by a camera from an Apple

Mobile Phone (iPhone 12, Apple Inc., California, USA) at a slow motion model with 240 fps. The phone was fixed on the shaking platform to keep it relatively stationary with the hollow OSRs.

To see the liquid more clearly, a certain amount of Methyl Red (1 M/L) and hydrochloric acid (1 M/L) was added before performing the capturing experiment. CFD MODEL Reynolds mean mass and

momentum conservation equations are used to control fluid flow (Eqs. (1), (2) and (3)): $$\begin{aligned} \frac{\partial \rho }{\partial t}+\triangledown \left( \rho V \right)= & {} 0

\end{aligned}$$ (1) $$\begin{aligned} \frac{\partial }{\partial t}\left( \rho V \right) +\triangledown \left( \rho VV \right)= & {} -\triangledown p+\triangledown \left( \tau \right)

+\rho \vec {g}+\vec {F} \end{aligned}$$ (2) $$\begin{aligned} \triangledown= & {} \frac{\partial }{\partial x} +\frac{\partial }{\partial y}+\frac{\partial }{\partial z} \end{aligned}$$

(3) where \(\rho \) refers to the density of the fluid (\(\mathrm {kg \, m^{-3}}\)), _p_ refers to the pressure (Pa), \(\tau \) refers to the shear stress (Pa), \(\rho \vec {g}\) and \(\vec

{F}\) refer to gravity and the external force, respectively, and _V_ represents the linear velocity vector. The shear stress can be obtained from Eq. (4): $$\begin{aligned} \tau =\sqrt{\tau

_{xy}^{2}+\tau _{yz}^{2} +\tau _{xz}^{2}} \end{aligned}$$ (4) where \(\tau _{xy} \), \(\tau _{yz}\), \(\tau _{xz}\) represent the three directions of shear stress. The three shear components

are determined as follows (Eqs. (5), (6) and (7)): $$\begin{aligned} \tau _{xy}= & {} \mu \left( \frac{\partial V_{x}}{\partial y}+\frac{\partial V_{y}}{\partial x} \right)

\end{aligned}$$ (5) $$\begin{aligned} \tau _{yz}= & {} \mu \left( \frac{\partial V_{y}}{\partial z}+\frac{\partial V_{z}}{\partial y} \right) \end{aligned}$$ (6) $$\begin{aligned} \tau

_{xz}= & {} \mu \left( \frac{\partial V_{x}}{\partial z}+\frac{\partial V_{z}}{\partial x} \right) \end{aligned}$$ (7) where \(\mu \) is the dynamic viscosity. THE VOLUMETRIC MASS

TRANSFER COEFFICIENT MODEL The volumetric mass transfer coefficient (\(k_{L}a\)) is crucial for the bioreactor, which analyzes key parameter of the oxygen transfer rate. The computed value

of \(k_{L}a\) was obtained by simulating the mass transfer coefficient ( \(k_{L}\)) and specific interface area (_a_) respectively. The specific interface area (_a_) can be obtained from Eq.

(8): $$\begin{aligned} a=\frac{A}{V_{L}} \end{aligned}$$ (8) where the _A_ is the interface area (m2) which could be obtained by the volume of fraction (VOF) model (see Table 1), and the

\(V_{L}\) is the filling volume (L). The mass transfer coefficient (\(k_{L}\)) can be obtained from Eq. (9): $$\begin{aligned} k_{L}=K\cdot \sqrt{D_{L}}\cdot \left( \frac{\varepsilon

}{\upsilon } \right) ^{\frac{1}{4}} \end{aligned}$$ (9) where \(K=\) 0.4 is the model constant, \(D_{L}\) is the diffusion coefficient of oxygen in the water \(\left( \mathrm {m^{2} \,

h^{-1}}\right) \), \(\varepsilon \) is the energy dissipation rate \(\left( \mathrm {m^{2} \, s^{-1}}\right) \) and \(\upsilon \) is the kinematic viscosity of water \(\left( \mathrm {m^{2}

\, s^{-1}}\right) \). ORBITALLY SHAKING MOVEMENT The orbital shaking motion naturally induces a homogeneous, rotating centrifugal force on the fluid20. This centrifugal force is considered

by adding the source term to the Navier-Stokes equations in the CFD model. The centrifugal forces in Eqs. (10) and (11) are given as follows: $$\begin{aligned} F_{x}= & {} \omega

^{2}R_{s}\cdot \mathrm {cos}\left( \omega t \right) \end{aligned}$$ (10) $$\begin{aligned} F_{y}= & {} \omega ^{2}R_{s}\cdot \mathrm {sin}\left( \omega t \right) \end{aligned}$$ (11)

where \(F_{x}\) and \(F_{y}\) represent the centrifugal force \(\left( \mathrm {m \, s^{-2}} \right) \) in the x and y directions, respectively. \(R_{s}\) represents the radius of shaking

(m), and \(\omega \) represents the angular velocity of shaking \(\left( \mathrm {rad \, s^{-1}} \right) \). SIMULATION CONDITIONS All simulations in this paper were performed in ANSYS

FLUENT 16.0 (ANSYS Inc., Canonsburg, PA, USA). In this paper, the volume of fluid (VOF) model was used to obtain the gas-liquid interface. The VOF model was employed to track the moving

gas-liquid interface21. The \(\mathrm {k-\omega -SST}\) turbulence model was used to enclose the governing equations of the fluid motion22. All the boundary conditions were set to the wall.

The PISO algorithm was used to solve the velocity and pressure. The time step size was 0.0001 seconds. The maximum courant number was 0.25. The grid for this hollow OSR was generated using

Gambit 2.4.6 (ANSYS Inc., Canonsburg, PA, USA). RESULTS AND DISCUSSION MODEL VALIDATION To test the influence of the mesh number on the simulated result, four different mesh numbers of

\(\mathrm {2.2\times 10^{6}}\), \(\mathrm {3.4\times 10^{6}}\), \(\mathrm {5.1\times 10^{6}}\) and \(\mathrm {7.0\times 10^{6}}\) were used to calculate the liquid height for the hollow OSR

with an h\(\mathrm {_{L}}\) of 0 mm. As the results show (Fig. 2), the liquid height curve would almost not change when the mesh number exceeded \(\mathrm {3.4\times 10^{6}}\), which

indicated that this mesh number (\(\mathrm {3.4\times 10^{6}}\)) was already sufficient to obtain stable and trustable simulation results. Thus, a mesh number of \(\mathrm {3.4\times

10^{6}}\) was used for all the simulations in this article. To validate the established CFD model, the calculated liquid wave height was compared with its measured values by a wave capturing

experiment. As shown in Fig. 3, the simulated and measured liquid wave shapes were similar. However, the simulated gas-liquid interface was found to be smoother than the experimental

observation. This drawback might be decreased by adopting a higher-order turbulence but with a penalty of a longer simulation time. By comparing the curves of the liquid wave in the

simulated and measured results, the wave height difference was found to be less than 15\(\%\), which indicated that the established CFD model was acceptable for use in analysing the fluid

dynamics of OSRs with hollow structures. FLOW FIELD The fluid velocity is the basic information for the flow field of a bioreactor, and it determines whether other derived fluid parameters

relevant to cell cultivation are correct. To generally understand the characteristics of this type of bioreactor, the fluid velocity distribution of the cylindrical OSR with an inner hollow

wall for the installation height of 30 mm (h\(_{\mathrm {L}}\) = 30 mm) is shown in Fig. 4. The maximum fluid velocity was found to be approximately 1.6 \(\mathrm {m \, s^{-1}}\) at the wave

front near the vessel wall, which was slightly higher than its theoretical maximum value of 1.57 \(\mathrm {m \, s^{-1}}\) from Eq. (12)2, which may be caused by local turbulence23.

$$\begin{aligned} V_{max}=2\pi rN \end{aligned}$$ (12) where \(V_{max}\) represents the theoretical maximum fluid velocity, _r_ represents the radius of the hollow cylindrical OSRs, and _N_

represents the shaking speed. Three vortices could be observed from the vertical section (A\(_{1}\)-A\(_{1}\)) in Fig. 4. The bulk fluid would be driven from the bottom of the bioreactor to

the top along those vortices. A vortex was located on the left side of the vertical section and was in an underdeveloped state. This might be because the amount of fluid was not sufficient

on this side. There is another subtle reason for this phenomenon, which was that the wave front was located at the left side with the maximum fluid velocity to transfer the mixing energy to

other fluid particles. Therefore, it is reasonable that only a limited amount of fluid particles can follow the wave front closely, which causes the fluid volume to be smaller near the wave

front. Two vortices were located at the wave crest side (right side). The larger one could drive fluid flowing along a larger circle (bottom to top) and was crucial for global fluid mixing

in OSRs. For the smaller vortex, it could increase the mixing intensity at the corner of the bioreactor where mixing is not good and even the “velocity dead zone” occurs easily. Therefore,

the existence of a smaller vortex was favourable for increasing the local mixing efficiency, which might explain why the velocity at the side corner of the wave trough is lower than that at

the side corner of the wave crest. It can be observed that the maximum velocity is near the wall of the hollow OSRs, and the fluid near the vessel wall has a high velocity because of the

high Froude numbers (\(F_{r}=V^{2}/\left( gl_{0} \right) \), where _V_ represents fluid velocity, _g_ represents gravity acceleration, and \(l_{0}\) represents characteristic length)24. The

Froude number is the key dimensionless driving parameter, which represents the driving capability25. The maximum velocity was located on the wall side of the wave trough rather than the wave

crest side. The mass transfer between the right and left vortices was also observed by the moving fluid in the middle of the bioreactor bottom. As Fig. 4A\(_{1}\)–A\(_{1}\) shows, the

percentage of fluid volume with different range velocities and fluid moving orientations are important for the energy exchange process. To analyse the mixing properties in horizontal planes,

the fluid velocity distributions were calculated on three different horizontal planes with different heights. As shown in Fig. 4B\(_{1}\)-B\(_{1}\), B\(_{2}\)-B\(_{2}\) and

B\(_{3}\)-B\(_{3}\), there was only one large vortex on the horizontal plane, and the vortex centre was almost identical to the plane centre.The high fluid velocity was found near the vessel

wall due to the high wall velocity, and the low fluid velocity was located at the vortex centre.It should be noted that the maximum fluid velocity also occurred at the wave front, as

mentioned before. EFFECT OF THE HOLLOW VESSEL WALL ON THE FLOW FIELD To analyse the effect of hollow vessel wall on the fluid dynamics of OSRs, simulations were conducted on several

cylindrical hollow OSRs with different installation heights with shaking speed of 100 rpm and filling volume of 8 L. In detail, the hollow vessel wall was installed at different positions

with h\(_{\mathrm {L}}\) = 0 mm (Fig. 5A), h\(_{\mathrm {L}}\) = 30 mm (Fig. 5B), h\(_{\mathrm {L}}\) = 60 mm (Fig. 5C), h\(_{\mathrm {L}}\) = 90 mm (Fig. 5D), and h\(_{\mathrm {L}}\) = 120

mm (Fig. 5E) away from the vessel bottom. In Fig. 5, it can be observed that there are three vortices in each vertical section. Similarly, a vortex lies on the side of the wave trough side

(the left side of the vertical section), which has not yet fully formed. The other two vortices were located on the wave crest side (the right side of the vertical section). The maximum

velocity can be observed at the wall of the trough for each case. For all the maximum velocities, the maximum value of 0.26 m/s was found at the hollow OSR with h\(_{\mathrm {L}}\) = 30 mm.

In fact, the magnitude of the bulk fluid velocity was also higher in the hollow OSR with h\(_{\mathrm {L}}\) = 30 mm (Fig. 5B) than in other cases. For the installation height of

h\(_{\mathrm {L}}\) = 120 mm (Fig. 5E), the flow field did not seem to change compared with the OSR without the hollow wall structure. The reason might be that there was only a small part of

the hollow cylinder contacting the moving fluid in the OSR with h\(_{\mathrm {L}}\) = 120 mm, which indicated that the hollow structure has almost no influence on fluid moving with 100 rpm

shaking speed and 8 L filling volume. With decreasing h\(_{\mathrm {L}}\), the contact area between the hollow structure and the moving fluid increased, and the fluid field started to

change. When h\(_{\mathrm {L}}\) decreased from 120 mm (Fig. 5E) to 60 mm (Fig. 5C), the fluid velocity in the vertical centre decreased gradually, which was caused by the hollow bottom

suppressing the fluid motion. This kind of resistance effect could inhibit the energy exchange process from the left vortex to the right vortex and was unfavourable for bulk mass transfer.

However, as h\(_{\mathrm {L}}\) decreased from 60 mm (Fig. 5C) down to 30 mm (Fig. 5B), the fluid velocity suddenly increased at the bioreactor centre part, and the region worked like a

“mass transfer tube” with a high speed, which was helpful for uniform mixing in the OSR. However, when the value of h\(_{\mathrm {L}}\) decreased to zero, the mass exchange among those

vortices at two sides was completely cut off, and some quite low fluid velocity region occurred near the hollow bottom, which probably meant that the nutrient supply would be insufficient at

the local region easily. For the vortices at the two sides, the magnitude of the fluid velocity increased steadily as h\(_{\mathrm {L}}\) decreased from h\(_{\mathrm {L}}\) = 120 mm to

h\(_{\mathrm {L}}\) = 30 mm, which might be caused by the hollow structure decreasing pushing more fluid into a high velocity state. However, the exchange among those vortices was completely

cut off when the value of h\(_{\mathrm {L}}\) decreased to zero, which caused the low fluid velocity near the hollow structure. Fig. 6 shows that the fluid velocity distributions were

similar. There was a large radial vortex on each section, and the maximum velocity was located at the wall, but the low fluid velocity occurred at the middle region near the vortex centre.

EFFECT OF THE HOLLOW VESSEL WALL EFFECT ON THE VOLUMETRIC MASS TRANSFER COEFFICIENT The volumetric mass transfer coefficient (\(k_{L}a\)) is crucial parameter for cell cultivation with a

high viable cell density. To compare the \(k_{L}a\) in the bioreactor with different installation heights, the mass transfer coefficient (\(k_{L}\)) and the specific interface area (_a_)

were simulated at different installation heights. As shown in Fig. 7, the values of \(k_{L}\) were nearly a constant for all the studied cases. Under the constant temperature cell culture

conditions (37), \(k_{L}\) will only depends on the turbulent dissipation rate (\(\varepsilon \)). Although different installation heights had different effects on the flow field, the value

of \(\varepsilon \) changed slightly at a fixed shaking speed (see Table 1). Therefore, the values of \(k_{L}\) almost did not change at different installation heights. The values of liquid

height (\(\Delta h\)) were calculated as shown in Table 1. The values of \(\Delta h\) remained almost constant at approximately 140 mm, which was slightly higher than the OSR without a

hollow baffle, suggesting that the liquid height mainly depended on the shaking speed. Thus, it could be concluded that the hollow baffle had limited influence on the liquid height and even

the slope of the wave shape. Due to the constant value of the filling volume, the value of the specific interface area only depends on the interface area. The values of _A_ remained almost

constant at approximately 0.07 \(\mathrm {m^{2}}\) for all the used installation heights (see Table 1), which was probably caused by the Froude number being the same at the fixed shaking

speed of 100 rpm. In detail, there was little difference in _A_ for different installation heights, and the reason for this could be that the interaction between the hollow wall and liquid

wave led to some interface area loss. As shown in Fig. 7, the values of \(k_{L}a\) and _a_ did not fluctuate greatly. In detail, the values of \(k_{L}a\) and _a_ had a consistent change

trend at different installation heights. When the value of the h\(_{\mathrm {L}}\) increased from h\(_{\mathrm {L}}\) = 0 mm to h\(_{\mathrm {L}}\) = 30mm, the magnitudes of the \(k_{L}a\)

and _a_ decreased slightly. However, the magnitudes of the \(k_{L}a\) and _a_ increased steadily as h\(_{\mathrm {L}}\) increased from h\(_{\mathrm {L}}\) = 30 mm to h\(_{\mathrm {L}}\) = 

120 mm. EFFECT OF THE HOLLOW CYLINDER OSR ON SHEAR STRESS Cell damage is a very important problem in bioreactors, but it is normally difficult to analyse26,27,28,29. Cell damage easily

occurs in a fluid environment with large shear stress values30. It was reported that a shear stress of 0.4 Pa was a critical value for CHO cells to suffer shear force31. To evaluate the

hydrodynamic stress environment in the hollow cylindrical OSRs, the shear stress distribution was calculated at a filling volume of 8 L and shaking speed of 100 rpm for the case with

h\(_{\mathrm {L}}\) = 30 mm (Fig. 8). The reason why the case with an hL of 30 mm was chosen was that the fluid velocity magnitude was higher and the mixing process was intense, as analysed

above. By observing the two horizontal Sections A\(_{1}\)-A\(_{1}\) and A\(_{2}\)-A\(_{2}\), the maximum shear stress was located at the outermost edge of the section for both cases. In

addition, it could also be seen that the shear stress in horizontal Section A\(_{2}\)-A\(_{2}\) was larger than that in Section A\(_{1}\)-A\(_{1}\). This might be because Section

A\(_{2}\)-A\(_{2}\) was closer to the vessel bottom than Section A\(_{1}\)-A\(_{1}\), and the fluid particles would be accelerated more easily near the vessel bottom wall. Meanwhile, the

maximum shear stress was found to be approximately 0.2 Pa in the whole vessel, which was lower than the critical value of 0.4 Pa of CHO cells, and large shear stress was located near the

wall of the vessel. The results suggested that the fluid environment of the hollow OSR was still gentle for mammalian cell cultivation. CONCLUSION This study was based on the

three-dimensional CFD model, and the reliability of the CFD model was verified by experiments. In this study, we analysed the influence of hollow cylindrical walls on the flow field at a

shaking speed of 100 rpm and a filling volume of 8 L. The results showed that the influence of hollow cylindrical walls at different installation heights on the \(k_{L}a\) was slight.

However,the results showed that the influence of hollow cylindrical walls at different installation heights on the flow field was different. When the installation height was 30 mm, the

low-speed zone in the middle region could be greatly reduced, and the mixing of the flow field could also be improved to promote the exchange of matter and energy. At the same time, it was

also concluded that the shear stress of the whole flow field was below 0.2 Pa, which was lower than the critical value of 0.4 Pa for CHO cells, indicating that the hollow bioreactor could

provide a gentle shear stress environment for mammalian cell cultivation. DATA AVAILIBILITY The datasets that pertain to the current study can be made available from the corresponding author

on reasonable request. ABBREVIATIONS * _A_ : Interface area (\(\mathrm {m^{2}}\)) * _a_ : The specific interface area (\(\mathrm {m^{-1}}\)) * CFD: Computational fluid dynamics * d: Outer

diameter (m) * d\(_{i}\) : Inner diameter (m) * \(\varepsilon \) : The energy dissipation rate \(\left( \mathrm {m^{2} \, s^{-1}}\right) \) * \(F_{x}\) : Centrifugal force in the x direction

(N) * \(F_{y}\) : Centrifugal force in the y direction (N) * \(\mathrm {g}\) : Gravity acceleration (\(\mathrm {m \, s^{-2}}\)) * \(\Delta h\) : Liquid height (m) * h\(_{\mathrm {L}}\) :

Installation height of inter cylinder wall (m) * k\(_{L}a\) : The volumetric mass transfer coefficient (\(\mathrm {h^{-1}}\)) * k\(_{L}\) : The mass transfer coefficient (\(\mathrm {m \,

h^{-1}}\)) * \(l_{0}\) : Characteristic length (m) * N: Shaking speed (rpm) * OSRs: Orbitally shaking bioreactors * _r_ : Radius of the hollow cylindrical OSRs (m) * \(R_{s}\) : Radius of

shaking (m) * STRs: Stirred tank bioreactors * _V_ : Fluid velocity (\(\mathrm {m \, s^{-1}}\)) * \(V_{max}\) : Theoretical maximum fluid velocity (\(\mathrm {m \, s^{-1}}\)) * \(V_{L}\) :

The filling volume (L) * VOF: Volume of fluid model * \(\omega \) : Angular velocity of shaking (\(\mathrm {rad \, s^{-1}}\)) REFERENCES * Weuster-Botz, D. High-throughput fermentation

process design with single-use stirred-tank bioreactors. _J. Biotechnol._ 136, 279–280. https://doi.org/10.1016/j.jbiotec.2008.07.599 (2008). Article  Google Scholar  * Kaiser, S. C.,

Kraume, M. & Eibl, D. Development of the travelling wave bioreactor—A concept study. _Chemie Ingenieur Technik_ 85, 136–143. https://doi.org/10.1002/cite.201200127 (2013). Article  CAS 

Google Scholar  * Rodriguez, G., Anderlei, T., Micheletti, M. & Eibl, D. On the measurement and scaling of mixing time in orbitally shaken bioreactors. _Biochem. Eng. J._ 82, 10–21.

https://doi.org/10.1016/j.bej.2013.10.021 (2013). Article  CAS  Google Scholar  * Shiue, A., Chen, S. C., Jeng, J. C. & Zhu, L. K. Mixing performance analysis of orbitally shaken

bioreactors. _Appl. Sci._ 10, 5597–5620. https://doi.org/10.1016/j.bej.2013.04.008 (2020). Article  CAS  Google Scholar  * Monteil, D. T., Tontodonati, G., Ghimire, S. & Hacker, D. L.

Disposable 600-ml orbitally shaken bioreactor for mammalian cell cultivation in suspension. _Biochem. Eng. J._ 76, 6–12. https://doi.org/10.1016/j.bej.2013.04.008 (2013). Article  CAS 

Google Scholar  * Bouvard, J., Herreman, W. & Moisy, F. Mean mass transport in an orbitally shaken cylindrical container. _Phys. Rev. Fluids_ 2, 1–17.

https://doi.org/10.1103/PhysRevFluids.2.084801 (2017). Article  Google Scholar  * Zhu, L. K., Han, W., Song, B. & Wang, Z. L. Characterizing the fluid dynamics in the flow fields of

cylindrical orbitally shaken bioreactors with different geometry sizes. _Eng. Life Sci._ 18, 570–578. https://doi.org/10.1007/s12110-009-9068-2 (2017). Article  Google Scholar  * Sucosky,

P., Osorio, D., Brown, J. & Neitzel, G. P. Fluid mechanics of a spinner-flask bioreactor. _Biotechnol. Bioeng._ 85, 34–46. https://doi.org/10.1002/bit.10788 (2004). Article  CAS  PubMed

  Google Scholar  * Lu, Z. M., Li, C. T., Brown, J. B. & Neitzel, G. P. Effect of baffle structure on flow field characteristics of orbitally shaken bioreactor. _Bioprocess Biosyst.

Eng._ 44, 563–573. https://doi.org/10.1007/s00449-020-02469-4 (2021). Article  CAS  PubMed  Google Scholar  * Zhang, X., Stettler, M., Reif, O., Kocourek, A. & DeJesus, M. Shaken helical

track bioreactors: Providing oxygen to high-density cultures of mammalian cells at volumes up to 1000 l by surface aeration with air. _New Biotechnol._ 25, 68–75.

https://doi.org/10.1016/j.nbt.2008.03.001 (2008). Article  CAS  Google Scholar  * Wang, L., Isobe, R., Okano, Y., Kino-Oka, M. & Matsuda, H. Bayesian optimization for hydrodynamic

characterization of a cylindrical orbitally shaken bioreactor with a bump at the bottom. _J. Chem. Eng. Jpn._ 54, 493–499. https://doi.org/10.1252/jcej.21we047 (2021). Article  CAS  Google

Scholar  * Kaiser, S. C., Kraume, M. & Eibl, D. Development of the travelling wave bioreactor. Part I: Design studies based on numerical models. _Chemie Ingenieur Technik_ 88, 77–85.

https://doi.org/10.1002/cite.201500092 (2016). Article  CAS  Google Scholar  * Discacciati, M., Hacker, D., Quarteroni, A. & Quinodoz, S. Numerical simulation of orbitally shaken viscous

fluids with free surface. _Int. J. Numer. Methods Fluids._ 71, 294–315. https://doi.org/10.1002/fld.3658 (2013). Article  ADS  MathSciNet  MATH  Google Scholar  * Luo, H. P. &

Al-Dahhan, M. H. Verification and validation of CFD simulations for local flow dynamics in a draft tube airlift bioreactor. _Chem. Eng. Sci._ 66, 907–923.

https://doi.org/10.1016/j.ces.2010.11.038 (2011). Article  CAS  Google Scholar  * Pruvost, J., Legrand, J. & Legentilhomme, P. Numerical investigation of bend and torus flows, part I:

Effect of swirl motion on flow structure in u-bend. _Chem. Eng. Sci._ 59, 3345–3357. https://doi.org/10.1016/j.ces.2004.03.040 (2004). Article  CAS  Google Scholar  * Rathore, A. S., Sharma,

C. & Persad, A. Use of computational fluid dynamics as a tool for establishing process design space for mixing in a bioreactor. _Biotechnol. Prog._ 28, 382–391.

https://doi.org/10.1002/btpr.745 (2012). Article  CAS  PubMed  Google Scholar  * Sharma, C., Malhotra, D. & Rathore, A. S. Review of computational fluid dynamics applications in

biotechnology processes. _Biotechnol. Prog._ 27, 1497–1510. https://doi.org/10.1002/btpr.689 (2011). Article  CAS  PubMed  Google Scholar  * Xia, J. Y., Wang, S. J., Zhang, S. L. &

Zhong, J. J. Computational investigation of fluid dynamics in a recently developed centrifugal impeller bioreactor. _Biochem. Eng. J._ 38, 406–413. https://doi.org/10.1016/j.bej.2007.08.006

(2008). Article  CAS  Google Scholar  * Zhu, L. K., Song, B. Y. & Wang, Z. L. Developing an orbitally shaken bioreactor featuring a hollow cylinder vessel wall. _J. Chem. Technol.

Biotechnol._ 94, 2212–2218. https://doi.org/10.1002/jctb.6005 (2019). Article  CAS  Google Scholar  * Horstmann, G. M., Herreman, W. & Weier, T. Linear damped interfacial wave theory for

an orbitally shaken upright circular cylinder. _J. Fluid Mech._ 891, 1–35. https://doi.org/10.1017/jfm.2020.163 (2020). Article  MathSciNet  MATH  Google Scholar  * Hirt, C. W. &

Nichols, B. D. Volume of fluid (VOF) method for the dynamics of free boundaries. _J. Comput. Phys._ 39, 201–225. https://doi.org/10.1016/0021-9991(81)90145-5 (1981). Article  ADS  MATH 

Google Scholar  * Menter, F. R. 2-equation eddy-viscosity turbulence models for engineering applications. _AIAA J._ 32, 1598–1605. https://doi.org/10.1016/0021-9991(81)90145-5 (1994).

Article  ADS  Google Scholar  * Stoots, C. M. & Calabrese, R. V. Mean velocity-field relative to a rushton turbine blade. _AIChE J._ 41, 1–11. https://doi.org/10.1002/aic.690410102

(1995). Article  CAS  Google Scholar  * Weheliye, W., Calabrese, R. V. & Ducci, A. On the fluid dynamics of shaken bioreactors-flow characterization and transition. _AIChE J._ 59,

334–344. https://doi.org/10.1002/aic.13943 (2013). Article  CAS  Google Scholar  * Buchs, J., Maier, U., Milbradt, C. & Zoels, B. Power consumption in shaking flasks on rotary shaking

machines: I. Power consumption measurement in unbaffled flasks at low liquid viscosity. _Biotechnol. Bioeng._ 68, 589–593.

https://doi.org/10.1002/(SICI)1097-0290(20000620)68:6<589::AID-BIT1>3.0.CO;2-J (2000). Article  CAS  PubMed  Google Scholar  * Cherry, R. S. & Papoutsakis, E. T.

Physical-mechanisms of cell-damage in microcarrier cell-culture bioreactors. _Biotechnol. Bioeng._ 32, 1001–1014. https://doi.org/10.1002/bit.260320808 (1988). Article  CAS  PubMed  Google

Scholar  * Kunas, K. T. & Papoutsakis, E. T. Damage mechanisms of suspended animal-cells in agitated bioreactors with and without bubble entrainment. _Biotechnol. Bioeng._ 36, 476–483.

https://doi.org/10.1002/bit.22263 (1990). Article  CAS  PubMed  Google Scholar  * Liu, Y., Li, F. X., Hu, W. W., Wiltberger, K. & Ryll, T. Effects of bubble-liquid two-phase turbulent

hydrodynamics on cell damage in sparged bioreactor. _Biotechnol. Prog._ 30, 48–58. https://doi.org/10.1002/btpr.1790 (2014). Article  CAS  PubMed  Google Scholar  * Lu, G. Z., Thompson, B.

G. & Gray, M. R. Physical modeling of animal-cell damage by hydrodynamic-forces in suspension-cultures. _Biotechnol. Bioeng._ 40, 1277–1281. https://doi.org/10.1002/bit.260401018 (1992).

Article  CAS  PubMed  Google Scholar  * Ducci, A. & Weheliye, W. H. Orbitally shaken bioreactors-viscosity effects on flow characteristics. _AIChE J._ 60, 3951–3968.

https://doi.org/10.1002/aic.14608 (2014). Article  CAS  Google Scholar  * Sorg, R., Tanzeglock, T., Soos, M. & Morbidelli, M. Minimizing hydrodynamic stress in mammalian cell culture

through the lobed Taylor-Couette bioreactor. _Biotechnol. J._ 6, 1504–1515. https://doi.org/10.1002/biot.201000477 (2011). Article  CAS  PubMed  Google Scholar  Download references FUNDING

This study was funded by Research cooperation project between Shenzhen university and National Taipei University of Technology-000003020328, Regional Joint Fund of Basic and Applied Basic

Research Fund of Guangdong Province-013376, and Open Project of State Key Laboratory of Management and Control of Complex Systems at the institute of Automation of Chinese Academy of

Sciences (No.20200107), National Natural Science Foundation of China (Grant Nos. 62003216), National Natural Science Foundation-Aerospace Joint Fund(Grant Nos. U2037205), Shenzhen Stability

Support Plan A (Grant Nos. 20200812104451001), Shenzhen Stability Support Plan A (Grant Nos. 20200814105908002) and Basic and Applied Basic Research Fund of Guangdong Province (Grant Nos.

2019A1515111115). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Shenzhen Key Laboratory of High Performance Nontraditional Manufacturing, College of Mechatronics and Control Engineering,

Shenzhen University, Shenzhen, 518060, China Likuan Zhu, Weiqing Chen & Chunyang Zhao Authors * Likuan Zhu View author publications You can also search for this author inPubMed Google

Scholar * Weiqing Chen View author publications You can also search for this author inPubMed Google Scholar * Chunyang Zhao View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS L.K.Z. designed the experiments and wrote the manuscript. W.Q.C. conducted the simulation and experiment. C.Y.Z. analyzed the simulated and experimental

data. CORRESPONDING AUTHOR Correspondence to Chunyang Zhao. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are

included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons

licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of

this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zhu, L., Chen, W. & Zhao, C. Analysis of hollow wall effect

on the fluid dynamics in the orbitally shaken bioreactors. _Sci Rep_ 12, 9596 (2022). https://doi.org/10.1038/s41598-022-13441-5 Download citation * Received: 26 February 2022 * Accepted:

24 May 2022 * Published: 10 June 2022 * DOI: https://doi.org/10.1038/s41598-022-13441-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative