News Reader.info

ABSTRACT Charge density wave (CDW) ordering has been an important topic of study for a long time owing to its connection with other exotic phases such as superconductivity and magnetism. The

\(R{\textrm{Te}}_{3}\) (_R_ = rare-earth elements) family of materials provides a fertile ground to study the dynamics of CDW in van der Waals layered materials, and the presence of

magnetism in these materials allows to explore the interplay among CDW and long range magnetic ordering. Here, we have carried out a high-resolution angle-resolved photoemission spectroscopy

(ARPES) study of a CDW material \({\textrm{Gd}}{\textrm{Te}}_{3}\), which is antiferromagnetic below \(\sim \mathrm {12~K}\), along with thermodynamic, electrical transport, magnetic, and

Raman measurements. Our ARPES data show a two-fold symmetric Fermi surface with both gapped and ungapped regions indicative of the partial nesting. The gap is momentum dependent, maximum

along \({\overline{\Gamma }}-\mathrm{\overline{Z}}\) and gradually decreases going towards \({\overline{\Gamma }}-\mathrm{\overline{X}}\). Our study provides a platform to study the dynamics

of CDW and its interaction with other physical orders in two- and three-dimensions. SIMILAR CONTENT BEING VIEWED BY OTHERS A BROKEN TRANSLATIONAL SYMMETRY STATE IN AN INFINITE-LAYER

NICKELATE Article 25 July 2022 ELECTRONIC LANDSCAPE OF KAGOME SUPERCONDUCTORS _A_V3SB5 (_A_ = K, RB, CS) FROM ANGLE-RESOLVED PHOTOEMISSION SPECTROSCOPY Article Open access 10 November 2023

CHARGE ORDER LANDSCAPE AND COMPETITION WITH SUPERCONDUCTIVITY IN KAGOME METALS Article 03 November 2022 INTRODUCTION Charge density wave (CDW)1,2 in quantum materials have been a subject of

numerous research works for a number of decades because of its relevance in understanding several physical properties and also its competition or coexistence with exotic phases like

superconductivity and magnetism3,4,5,6,7,8,9,10,11,12,13,14. CDW ordering is a phenomenon associated with Fermi surface (FS) instabilities, where a periodic lattice distortion leads to the

spatial modulation of carrier density2. One example is the Peierls distortion in one-dimension15,16, in which the lattice periodicity can be doubled by electronically disturbing the system

with a wave vector that is double the Fermi wave number, resulting into a gap opening at the Brillouin zone (BZ) boundaries nested by the same wave vector (FS nesting). With increase in

dimensions, the FS nesting tends to be imperfect so that certain regions of the FS remain ungapped, leading to a metallic nature17,18. The mechanism of CDW in such higher-dimensional

materials is still of great interest as it can differ from material to material, can have different origin, and also depends on crystal growth conditions19,20,21,22. The orthorhombic

crystalline family of van der Waals layered materials \(R{\textrm{Te}}_{3}~(R~=~\mathrm {rare-earth~elements})\) has been broadly studied for the presence of CDW23,24,25,26,27. The CDW

ordering takes place at a high temperature, and materials with heavier rare-earth elements exhibit a second CDW transition at a lower temperature28,29. In addition, the existence of long

range magnetic ordering in these compounds provides ground to study the interplay among magnetic and CDW orders30,31. \(R-\textrm{Te}\) slabs are sandwiched in between planar bi-layers of

\(\textrm{Te}-\textrm{Te}\), where the neighboring \(\textrm{Te}-\textrm{Te}\) are connected through weak van der Waals interaction, thereby easing the exfoliation of these layered materials

to the two-dimensional limit32,33,34,35. Angle-resolved photoemission spectroscopy (ARPES)36,37 has been a useful tool to directly probe the energy-momentum dispersion in quantum materials.

It has been extensively used to study the electronic structure of \(R{\textrm{Te}}_{3}\) in the investigation of FS and CDW induced gap17,38,39,40,41,42,43,44,45,46,47. The gap size is

found to depend on momentum, and the maximum gap changes as a function of the rare-earth element _R_, which can be modeled by a nesting driven sinusoidal CDW40. Among the materials under

this family, \({\textrm{Gd}}{\textrm{Te}}_{3}\) has been reported to have very high electronic mobility33 and steep band dispersion at the Fermi level45. It can be thinned down to ultrathin

limit using mechanical exfoliation that allows to study the thickness dependence of the CDW ordering32,33. Properties such as CDW ordering, magnetic ordering, and pressure induced

superconductivity28,31,48 make this system interesting in order to explore more on the electronic properties. In this communication, by utilizing high-resolution ARPES measurements, we study

the electronic structure of layered van der Waals material \({\textrm{Gd}}{\textrm{Te}}_{3}\). Our thermodynamic and electrical transport measurements show that the material is

antiferromagnetic (AFM), with the magnetic transition occurring below \(\sim \mathrm {12~K}\). The CDW transition occurs well above room temperature, at around \(\sim \mathrm {375~K}\). Our

ARPES results show two-fold symmetric FS with spectral intensity absent around certain regions of the FS, especially around \({\overline{\Gamma}}-\mathrm{\overline{M}}\) to

\({\overline{\Gamma}}-\mathrm{\overline{Z}}\), indicating the presence of gap at the Fermi level. Some regions of the FS near the \(\mathrm {\overline{X}}\) point remain gapless, implying

partial nesting. This gap is strongly direction dependent, with a gap maximum along \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) and gradually decreasing towards

\({\overline{\Gamma}}-\mathrm{\overline{X}}\). The room temperature Raman spectroscopy measurement shows the presence of CDW amplitude mode in the bulk as well as ultrathin samples up to 4L

(\(\sim \mathrm {5~nm}\)). Our results indicate that this material is excellent for studying the dynamics and interaction of CDW with other physical parameters in both three- and

two-dimensional limits. RESULTS CRYSTAL STRUCTURE AND BULK PROPERTIES MEASUREMENTS \({\textrm{Gd}}{\textrm{Te}}_{3}\) crystallizes in a layered orthorhombic structure (space group Number 63)

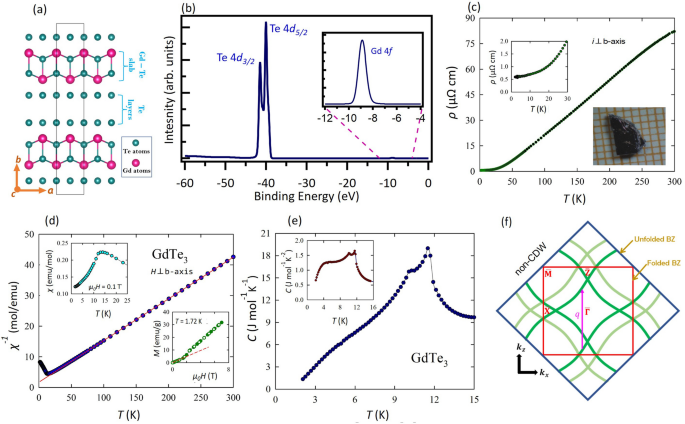
with lattice parameters \(a \approx c \approx \mathrm {4.33~{\text{\AA }}}\) and \(b = \mathrm {25.28~\text{\AA }}\), close to the values reported in literature33. In Fig. 1a, we present

the side view of the crystal structure of \({\textrm{Gd}}{\textrm{Te}}_{3}\), where pink balls represent the gadolinium atoms and teal colored balls represent the tellurium atoms. The

crystal structure is composed of \(\mathrm {Gd - Te}\) slabs sandwiched in between the \(\textrm{Te}\) bi-layers. Neighboring \(\textrm{Te}\) layers are bonded by weak van der Waals

interaction, and the natural cleaving plane is parallel to the _ac_ plane—the (010) plane. In Fig. 1b, we show the spectroscopic core level spectrum, where peaks associated with

\(\textrm{Te}\) 4_d_ and \(\textrm{Gd}\) 4_f_ can be clearly identified. \({\textrm{Gd}}{\textrm{Te}}_{3}\) exhibits a CDW phase transition, with the transition temperature well above room

temperature (\(\sim \mathrm {377~K}\))28. In addition, it also undergoes an AFM transition at a low temperature of \(\sim \mathrm {12~K}\)31,33,49. Our heat capacity (_C_) measurements also

show an anomaly near \(\mathrm {375~K}\) (see Supplementary Note 1 & Supplementary Fig. 1] that arises due to the incommensurate charge density wave formation27. The room temperature

Raman spectrum for the bulk crystal shows a CDW amplitude mode along with other phonon modes, in concert with the literature32,51, establishing the presence of room-temperature CDW in the

material. The mode remains prominent when the bulk crystal is thinned down to 4-layered samples via gold-assisted mechanical exfoliation, which suggests this material to be an excellent

platform to study the interplay of CDW and long-range orders down to the two-dimensional limit as well [see Supplementary Note 2 & Supplementary Fig. 2]. Figure 1c displays the

temperature dependence of the electrical resistivity (\(\rho\)) of \({\textrm{Gd}}{\textrm{Te}}_{3}\) measured with electrical current flowing in the crystallographic _ac_-plane. In concert

with the previous reports28,31,33, single crystals of \({\textrm{Gd}}{\textrm{Te}}_{3}\) investigated in the present study exhibit very good metallic-type charge conductance. The ratio of

the resistivity values measured at \(\mathrm {300~K}\) and \(\mathrm {2~K}\) is as large as \(\textrm{140}\), thus indicating high crystalline quality of the samples. On approaching the room

temperature, the \(\rho (T)\) curve clearly changes its slope signaling the proximity of the CDW transition. Figure 1d displays the temperature dependence of the inverse magnetic

susceptibility (\(\chi ^{-1}\)) measured for magnetic field applied perpendicular to the crystallographic _b_-axis. Above about \(\mathrm {30~K}\), \(\chi ^{-1}(T)\) exhibits a straight line

behavior that can be approximated by the Curie-Weiss formula with the effective magnetic moment \(\mu _{eff} = \mathrm {7.67~\mu _B}\) and the paramagnetic Curie temperature \(\theta _p =

\mathrm {-12.6~K}\). The value of \(\mu _{eff}\) is close to the theoretical prediction for \(\textrm{Gd}^{3+}\) ion. The negative value of \(\theta _p\) reflects the predominance of AFM

exchange interactions, which bring about the long range AFM ordering below about \(\mathrm {12~K}\) (see the upper inset to Fig. 1d). The AFM nature of the electronic ground state in

\({\textrm{Gd}}{\textrm{Te}}_{3}\) is further corroborated by the characteristic behavior of the magnetization isotherm taken at \(T = \mathrm {1.72~K}\) (see the lower inset in Fig. 1d)

with a clear metamagnetic transition near \(\mathrm {1.5~T}\). Overall, the magnetic data collected in our study agrees very well with those reported in the literature30,33,49. We also

observed a distinct lambda-shaped anomaly at around \(\mathrm {11.6~K}\) in _C_(_T_) graph, followed by a subsequent feature observed at \(\mathrm {10~K}\) (Fig. 1e), similar to previous

reports31,33,49. EXPERIMENTAL OBSERVATION OF THE CDW GAP In Fig. 1e, we present a schematic of the non-CDW FS of \(R\textrm{Te}_3\). The bands crossing the Fermi level come from the _p_

orbitals of the atoms within the \(\textrm{Te}\) layers. The two-dimensional unfolded band structure (dark green bands referred to as main bands hereafter) corresponds to ”true” square

lattice with one \(\textrm{Te}\) atom in the primitive unit cell. Such unit cell can be obtained by \(\sqrt{2}\) times reduction and \({45}^{\circ }\) rotation of the unit cell of the whole

crystal structure. To account for the three-dimensional lattice symmetry, the FS is acquired by considering the folding of the bands in the \(\textrm{Te}\) plane leading to the folded BZ

represented by the red square in Fig. 1e. The band folding is reflected on the observed band structure, where the mismatch between bands lead to their occurrence as the low intensity shadow

bands 40,42. In Fig. 1e, \(q = \frac{5}{7}c^*\) represents a nesting condition, where the wave vector nests two sets of the main bands, which would still be present if we only consider the

two-dimensional unit cell of the \(\textrm{Te}\) plane without folding. The constant energy contours obtained at the FS and at various binding energies using a photon source of energy

\(\mathrm {90~eV}\) (\(T = \mathrm {8~K}\)) are presented in Fig. 2. The BZ represented by the dashed red lines is obtained from the (010) surface projection of the three-dimensional BZ. As

seen in Fig. 2a, the FS is metallic, in agreement with the metallic nature observed in the transport measurements, and is two-fold symmetric. Strong photoemission intensity is observed at

the Fermi level along and around the \({\overline{\Gamma}}-\mathrm{\overline{X}}\) direction. However, the intensity for the main bands along the

\({\overline{\Gamma}}-\mathrm{\overline{M}}\) and \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions is missing. On going to lower binding energy of about \(\mathrm {100~meV}\), the

intensity of the main bands starts to fill up towards the \({\overline{\Gamma}}-\mathrm{\overline{M}}\) line, however, a gap still exists along the

\({\overline{\Gamma}}-\mathrm{\overline{M}}\) and \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions. The main band intensity only fills up along the

\({\overline{\Gamma}}-\mathrm{\overline{M}}\) line at around \(\sim \mathrm {140~meV}\) binding energy and along the \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) line at \(\sim \mathrm

{310~meV}\) binding energy. These results indicate that a gap exists at the Fermi level along the \({\overline{\Gamma}}-\mathrm{\overline{M}}\) and

\({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions. Similar nature of the gap was obtained in different set of measurements performed using \(\mathrm {68~eV}\) incident photon energy,

in which the main band intensity appears along the \({\overline{\Gamma}}-\mathrm{\overline{M}}\) and \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions, only around the binding

energies of \(\sim \mathrm {150~meV}\) and \(\sim \mathrm {320~meV}\) binding energies, respectively [see Supplementary Note 3 & Supplementary Fig. 3]. In Fig. 2h, we present the

theoretically calculated FS (without considering CDW), which is similar to the one presented in Fig. 1e. To compare with the theoretical FS, we present the experimental energy contour in

Fig. 1e, which is integrated up to \(\sim \mathrm {300~meV}\) binding energy. Main bands as well as the shadow bands (from the folding), as previously described, can be observed. In addition

to the low intensity bands coming from the folding of the three-dimensional BZ, we also observe other faint bands (shown by magenta colored arrows and traced by magenta colored curves) that

are not captured in the calculations [Also see Supplementary Note 4 and Supplementary Fig. 4]. These bands arise as a result of the CDW ordering. In order to quantify the gap along the

\({\overline{\Gamma}}-\mathrm{\overline{M}}\) and \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions, we took cuts along these directions and analyzed the corresponding band

dispersion. In Fig. 3a, we present the dispersion map along \({\overline{\Gamma}}-\mathrm{\overline{M}}\) obtained using a photon source of \(\mathrm {68~eV}\) at a temperature of \(\mathrm

{8~K}\). From the band dispersion, there exists a gap along this direction line with the absence of photoemission signal in the FS. The second derivative plot of the band dispersion

presented in Fig. 3b shows that the bands extend up to the binding energy of about \(\sim \mathrm {150~meV}\), and a clear gap exists above this binding energy along the

\({\overline{\Gamma}}-\mathrm{\overline{M}}\) direction. The gap of about \(\mathrm {150~meV}\) below the Fermi level can also be seen from the Fermi fit of the leading edge in the energy

distribution curve (Fig. 3c) taken within the momentum window represented by the magenta colored solid line in Fig. 3a. Next, we turn our attention to explore the gap along

\({\overline{\Gamma}}-\mathrm{\overline{Z}}\). From the dispersion map (Fig. 3d), its second derivative (Fig. 3e), and the Fermi fit of the leading edge in energy distribution curve (Fig. 

3f), it is clear that a gap below the Fermi level of about \(\sim \mathrm {320~meV}\) exists along this direction. The dispersion maps for \(\mathrm {90~eV}\) incident photon energy are

presented in the Supplementary Fig. 5 [also see Supplementary Note 5], which show that gaps along the \({\overline{\Gamma}}-\mathrm{\overline{M}}\) and

\({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions are \(\sim \mathrm {140~meV}\) and \(\sim \mathrm {310~meV}\), respectively, as observed in the energy contours presented in Fig. 2.

The calculated band structures along these directions well reproduce the experimental data barring the CDW induced gap as the calculations are carried out for the non-CDW case. ARPES can

only probe up to the Fermi energy, so the value of the total gap size can not be obtained from the ARPES measurements. Along \({\overline{\Gamma}}-\mathrm{\overline{X}}\) and

\(\mathrm{\overline{M}}-\mathrm{\overline{X}}\), however, bands cross the Fermi level [Fig. 3g,h; also see Supplementary Note 6 & supplementary Fig. 6], which is in accordance with the

photoemission intensity observed along this direction in the energy contours in Fig. 2. MOMENTUM DEPENDENCE OF THE CDW GAP BELOW THE FERMI LEVEL From the observations in Figs. 2 and 3, we

get the idea that the spectral intensity corresponding to the main bands appears at lower and lower binding energies as we move from \({\overline{\Gamma}}-\mathrm{\overline{X}}\) to

\({\overline{\Gamma}}-\mathrm{\overline{Z}}\). In Fig. 4, we analyze this momentum dependence of the gap below the Fermi level in measurements using a photon energy of \(\mathrm {68~eV}\) as

a function of counter-clockwise angle from the \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) direction. \(\mathrm {0^{\circ }}\) corresponds to the

\({\overline{\Gamma}}-\mathrm{\overline{Z}}\) direction and a \(\mathrm {45^{\circ }}\) counter-clockwise rotation means we are looking at the \({\overline{\Gamma}}-\mathrm{\overline{M}}\)

direction. Figure 4b represents the leading edges in the integrated energy distribution curves for dispersion maps corresponding to different angles defined in Fig. 4a. It is clear that the

leading edge shifts towards the Fermi level when we take the dispersion map away from the \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) direction towards the

\({\overline{\Gamma}}-\mathrm{\overline{X}}\) direction, indicative of reducing gap below the Fermi level. At an angle of \(\mathrm {62~^{\circ }}\), the gap size surpasses the limits of the

experimental energy resolution, therefore, it can be anticipated that the gap vanishes at greater angles [also see Supplementary Note 7 & Supplementary Fig. 7]. In Fig. 4c, we plot the

gap below the Fermi level as a function of the counter-clockwise angle from \({\overline{\Gamma}}-\mathrm{\overline{Z}}\), where with angle, the gap gradually reduces from around \(\mathrm

{320~meV}\) at \(\mathrm {0^{\circ }}\) to around \(\mathrm {150~meV}\) at \(\mathrm {45^{\circ }}\), i.e., \({\overline{\Gamma}}-\mathrm{\overline{M}}\) direction and reaches out of

experimental resolution at angles greater than \(\mathrm {62^{\circ }}\). DISCUSSION Given the existence of CDW ordering and AFM ordering in \(R\textrm{Te}_3\) materials, in which 4_f_

electrons coming from the _R_-element may bring electronic correlations into play, these materials are excellent platforms to study the interplay among electronic interactions, CDW, and

long-range magnetic orders. The layered nature of the crystal structure with very weak van der Waals interaction provides opportunity to study such interplay in both three- and

two-dimensions as mechanically exfoliating the crystals to the two-dimensional limit is easy. In this study, we studied bulk crystals of one of such materials \(\textrm{Gd}\textrm{Te}_3\),

which exhibits CDW transition at \(\sim \mathrm {375~K}\) and the magnetic ordering onsets below \(\sim \mathrm {12~K}\)10,28,31,33,49. The \(\textrm{Gd}~4f\) states are well below the Fermi

level as seen in the spectroscopic core level measurement. We were able to obtain thin flakes of \(\textrm{Gd}\textrm{Te}_3\) via mechanical exfoliation, which still showed prominent CDW

amplitude peak in the Raman spectrum taken at room temperature, indicating the presence of high-temperature CDW in the ultrathin limit as well. In fact, the CDW transition temperature is

expected to increase with lowering of the sample thickness32. The FS obtained from ARPES measurement is two-fold symmetric. This two-fold symmetry instead of four-fold symmetry is as a

result of slightly greater _c_ than _a_ (\(c-a\sim \mathrm {0.01~\text{\AA }}\)33), and this changes possible two degenerate CDWs along _a_ and _c_ axes in favor of a single CDW along _c_

direction with a CDW wave-vector \(q_{CDW} = \frac{2}{7}c^*\)23,26,28. This wave vector connects the inner and outer diamond sheets in the FS, formed by the unfolded and folded band

structures, respectively. An equivalent wave vector \(q = c^*-q_{CDW} = \frac{5}{7}c^*\) nests the FS made by the main bands coming from a ”true” two-dimensional plane of \(\textrm{Te}\)

atoms and therefore would be present even if the effects of the band folding scenario are not considered28,38,50. In our experimental data, the FS features coming from the shadow folded

bands seem to be present even at the FS, however, the main band intensity is only along and around the \({\overline{\Gamma}}-\mathrm{\overline{X}}\) direction and absent going away from this

direction around \({\overline{\Gamma}}-\mathrm{\overline{M}}\) and \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) directions. Therefore, our study shows that the CDW gap in

\(\textrm{Gd}\textrm{Te}_3\) is governed by the nesting condition \(q = \frac{5}{7}b^{*}\). Probing of the CDW gap is restricted to below the Fermi level, as the ARPES spectral function

depends upon Fermi-Dirac function, which is zero above the Fermi energy. The gap below the Fermi level is strongly dependent on the direction along which we take the dispersion map - it is

highest along \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) and reduces gradually towards \({\overline{\Gamma}}-\mathrm{\overline{X}}\), vanishing before reaching

\({\overline{\Gamma}}-\mathrm{\overline{X}}\) line. Such a nature of the gap occurs in nesting driven CDW when the nesting is imperfect and has been reported in a previous study on

\(R{\textrm{Te}}_{3}\) which reports the nesting to become imperfect away from \(k_x = 0\)40. Measurement performed at a different temperature of \(\mathrm {15~K}\) (conducted at a different

beamline setup) reveals similar dependence on momentum (see Supplementary Fig. 8). In addition to the CDW induced gap, we are able to identify some features that can not be described in the

non-CDW FS with main and folded bands. These features also appear as shadow-like bands with weak intensity and are expected to originate due to the reconstruction caused by the CDW

ordering. To conclude, we studied a van der Waals layered material, \({\textrm{Gd}}{\textrm{Te}}_{3}\), by performing high-resolution ARPES measurements of the electronic structure. We were

able to probe the CDW induced gap as well as band features originating from the CDW ordering-induced reconstruction. The gap obtained in our study is strongly dependent on the momentum

direction with the highest gap lying along the \({\overline{\Gamma}}-\mathrm{\overline{Z}}\) direction. A prominent peak associated with the CDW amplitude mode is seen in our Raman

measurements in samples as thin as 4L. Overall, our study demonstrates that \({\textrm{Gd}}{\textrm{Te}}_{3}\) is an excellent material platform to investigate the dynamics of CDW and its

connection with other physical orders like magnetism and superconductivity as a function of sample thickness ranging from three- to two-dimensions. METHODS CRYSTAL GROWTH AND

CHARACTERIZATION High-quality single crystals of \(\textrm{Gd}\textrm{Te}_3\) were synthesized using the self-flux technique, as described in the literature52. Chemical composition and phase

homogeneity of the crystals were determined by means of energy-dispersive x-ray (EDX) analysis performed using a FEI scanning electron microscope equipped with an EDAX Genesis XM4

spectrometer. The specimens examined were found homogeneous and single-phase. The crystal structure was verified by powder x-ray diffraction (XRD) made on finely pulverized crystals

employing a PANanalytical X’pert Pro diffractometer with \(\mathrm {Cu~K_\alpha }\) radiation. The XRD data was evaluated using the Rietveld method and the FULLPROF software package. The

result confirmed the orthorhombic structure (space group _#63_) and yielded the lattice parameters \(a \approx c \approx \mathrm {4.33~\text{\AA }}\), \(b = \mathrm {25.3~\text{\AA }}\),

close to values reported in literature33. In addition, the single crystal selected for physical properties measurements was examined on an Oxford Diffraction X’calibur four-circle

single-crystal x-ray diffractometer equipped with a CCD Atlas detector. THERMODYNAMIC AND ELECTRICAL TRANSPORT MEASUREMENTS Magnetic properties were investigated from \(\mathrm {1.72~K}\) to

\(\mathrm {300~K}\) and in magnetic fields up to \(\mathrm {7~T}\), applied perpendicular to the crystallographic _b_-axis, using a Quantum Design MPMS-XL superconducting quantum

interference device (SQUID) magnetometer. The heat capacity was measured in the temperature interval \(\mathrm {2-400~K}\) employing the relaxation technique and two-\(\tau\) model

implemented in a Quantum Design PPMS-9 platform. Electrical transport measurements were performed on a bar-shaped specimen cut from the oriented crystal using a wire saw. Electrical contacts

were made by silver wires of diameter \(\mathrm {20~\mu m}\), attached to the specimen’s surface in a linear manner with a single-component silver paste. The experiments were carried out in

the same PPMS platform in the temperature range \(\mathrm {2-300~K}\) employing a standard four-points ac technique and electrical current flowing within the crystallographic _ac_-plane.

RAMAN SPECTROSCOPY MEASUREMENTS Raman spectroscopy measurements were performed in ambient conditions using a Horiba LabRAM HR Evolution Spectrometer equipped with a \(\mathrm

{1800~grooves/mm}\) grating and a Synapse EMCCD detector. A frequency doubled Nd:YAG \(\mathrm {532~nm}\) excitation laser source was focused to a square micron sized beam spot using an

\(\mathrm {100\times }\) objective. An ultra-low-frequency (ULF) filter was utilized to resolve the CDW peak at low wavenumbers. SPECTROSCOPIC CHARACTERIZATION High-resolution ARPES

measurements were performed at the Stanford Synchrotron Radiation Lightsource (SSRL) end-station 5-2 and at the Advanced Light Source (ALS) beamline 10.0.1.2, both equipped with a DA30

electron analyzer. The angular and energy resolutions were set better than \(\mathrm {0.2^{\circ }}\) and \(\mathrm {20~meV}\), respectively. The samples, mounted on copper posts and

attached to ceramic posts on top using silver epoxy paste, were loaded and cleaved _in situ_ inside the ARPES chamber maintained under ultra high vacuum better than \(\mathrm

{10^{-10}~torr}\). Measurements at SSRL were carried out at a temperature of \(\mathrm {8~K}\) and those at ALS were performed at \(\mathrm {15~K}\). COMPUTATIONAL DETAILS The

first-principles calculations based on density-functional theory (DFT)53,54 were performed using the projector augmented-wave (PAW) potentials 55 implemented in the QuantumESPRESSO56,57,58.

The calculations were performed within the generalized gradient approximation (GGA) in the Perdew, Burke, and Ernzerhof (PBE) parameterization59, develop within PsLibrary60. The atom

position was optimized for conventional unit cell with experimental values of lattice vectors, using the \(\textrm{14} \times \textrm{2} \times \textrm{14}\) K–point grid in the

Monkhorst–Pack scheme 61. As the convergence condition for the optimization loop, we took the energy difference of \(\mathrm {10^{-6}~eV}\). The calculations were performed with the energy

cut-off set to \(\mathrm {400~eV}\). In calculations, the \(\textrm{Gd}~4f\) electrons were treated as valence states. To theoretical study of electronic band structure, we use the tight

binding model in the maximally localized Wannier orbitals basis 62,63. This model was constructed from exact DFT calculations in a conventional unit cell, with \(\textrm{6} \times \textrm{2}

\times \textrm{6}\) \(\Gamma\)-centered K–point grid, using the Wannier90 software 64. The tight binding (\(\textrm{28}\) orbitals \(\textrm{112}\) bands) model is based on _d_ orbitals of

\(\textrm{Gd}\), and _p_ orbitals of \(\textrm{Te}\). Finally, the energy-momentum spectra of the system were calculated using the surface Green's function technique for a semi-infinite

system65, implemented in WannierTools66. REFERENCES * Grüner, G. The dynamics of charge-density waves. _Rev. Mod. Phys. _60, 1129. https://doi.org/10.1103/RevModPhys.60.1129 (1988). Article

  ADS  Google Scholar  * Grüner, G. _Density Waves in Solids_ (Addison-Wesley, 1994). Google Scholar  * Morris, R. C. Connection between charge-density waves and superconductivity in 

\({\text{Nb}}{\text{Se}}_{2}\). _Phys. Rev. Lett._ 34, 1164. https://doi.org/10.1103/PhysRevLett.34.1164 (1975). Article  ADS  CAS  Google Scholar  * Gabovich, A. M. & Voitenko, A. I.

Superconductors with charge- and spin-density waves: Theory and experiment (Review). _Low Temp. Phys._ 26, 305. https://doi.org/10.1063/1.593902 (2000). Article  ADS  CAS  Google Scholar  *

Jung, M. H., Ekino, T., Kwon, Y. S. & Takabatake, T. Tunneling spectroscopy of \(R{\text{Te}}_{2} (R=\text{La},\text{Ce})\) and possible coexistence between charge-density waves and

magnetic order. _Phys. Rev. B_ 63, 035101. https://doi.org/10.1103/PhysRevB.63.035101 (2000). Article  ADS  CAS  Google Scholar  * Gabovich, A. M., Voitenko, A. I., Annett, J. F. &

Ausloos, M. Charge- and spin-density-wave superconductors. _Supercon. Sci. Technol._ 14, R1. https://doi.org/10.1088/0953-2048/14/4/201 (2001). Article  ADS  CAS  Google Scholar  * Yokoya,

T. _et al._ Fermi surface sheet-dependent superconductivity in \(2H-\text{NbSe}_2\). _Science_ 294, 2518. https://doi.org/10.1126/science.1065068 (2001). Article  ADS  CAS  PubMed  Google

Scholar  * Galli, F. _et al._ Coexistence of charge density wave and antiferromagnetism in \(\text{Er}_5\text{Ir}_4\text{Si}_{10}\). _J. Phys. Condens. Matter_ 14, 5067.

https://doi.org/10.1088/0953-8984/14/20/302 (2002). Article  ADS  CAS  Google Scholar  * Jung, M. H. Superconductivity in magnetically ordered \({\text{ CeTe}}_{1.82}\). _Phys. Rev. B_ 67,

212504. https://doi.org/10.1103/PhysRevB.67.212504 (2003). Article  ADS  CAS  Google Scholar  * Iyeiri, Y., Okumura, T., Michioka, C. & Suzuki, K. Magnetic properties of rare-earth metal

tritellurides \(R{\text{Te}}_{3}\)\((R=\text{ Ce },\text{ Pr },\text{ Nd },\text{ Gd },\text{ Dy})\). _Phys. Rev. B_ 67, 144417. https://doi.org/10.1103/PhysRevB.67.144417 (2003). Article 

ADS  CAS  Google Scholar  * Singh, Y., Nirmala, R., Ramakrishnan, S. & Malik, S. K. Competition between superconductivity and charge-density-wave ordering in the

\({\text{Lu}}_{5}{\text{Ir}}_{4}{({\text{Si}}_{1-x}{\text{Ge}}_{x})}_{10}\) alloy system. _Phys. Rev. B_ 72, 045106. https://doi.org/10.1103/PhysRevB.72.045106 (2005). Article  ADS  CAS 

Google Scholar  * Fang, L. _et al._ Competition of superconductivity and charge density wave order in \(\text{Na}_x\text{Ta}\text{S}_2\) single crystals. _Sci. Technol. Adv. Mater._ 6, 736.

https://doi.org/10.1016/j.stam.2005.06.005 (2005). Article  CAS  Google Scholar  * Hossain, Z. _et al._ Coexistence of magnetic order and charge density wave in a Kondo lattice:

\({\text{Yb}}_{5}{\text{Ir}}_{4}{\text{Si}}_{10}\). _Phys. Rev. B_ 71, 060406(R). https://doi.org/10.1103/PhysRevB.71.060406 (2005). Article  ADS  CAS  Google Scholar  * Shimomura, S. _et

al._ Charge-density-wave destruction and ferromagnetic order in \({\text{Sm}}{\text{Ni}}{\text{C}}_{2}\). _Phys. Rev. Lett._ 102, 076404. https://doi.org/10.1103/PhysRevLett.102.076404

(2009). Article  ADS  CAS  PubMed  Google Scholar  * Peierls, R. & Peierls, R. E. _Quantum Theory of Solids_ (Oxford University Press, 1955). MATH  Google Scholar  * Ashcroft, N. W.

& Mermin, N. D. _Solid State Physics_ (Cengage Learning, 1976). MATH  Google Scholar  * Gweon, G.-H. _et al._ Direct observation of complete fermi surface, imperfect nesting, and gap

anisotropy in the high-temperature incommensurate charge-density-wave compound \({\text{Sm}}{\text{Te}}_{3}\). _Phys. Rev. Lett._ 81, 886. https://doi.org/10.1103/PhysRevLett.81.886 (1998).

Article  ADS  CAS  Google Scholar  * Garcia, D. R. _et al._ Revealing charge density wave formation in the \({\text{La}}{\text{Te}}_{2}\) system by angle resolved photoemission spectroscopy.

_Phys. Rev. Lett._ 98, 166403. https://doi.org/10.1103/PhysRevLett.98.166403 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Johannes, M. D. & Mazin, I. I. Fermi surface nesting

and the origin of charge density waves in metals. _Phys. Rev. B_ 77, 165135. https://doi.org/10.1103/PhysRevB.77.165135 (2008). Article  ADS  CAS  Google Scholar  * Zhu, X., Guo, J., Zhang,

J. & Plummer, E. W. Misconceptions associated with the origin of charge density waves. _Adv. Phys. X_ 2, 622. https://doi.org/10.1080/23746149.2017.1343098 (2017). Article  CAS  Google

Scholar  * Thorne, R. E. Effect of crystal-growth conditions on charge-density-wave pinning in \({\text{Nb}}{\text{Se}}_{3}\). _Phys. Rev. B_ 45, 5804.

https://doi.org/10.1103/PhysRevB.45.5804 (1992). Article  ADS  CAS  Google Scholar  * Sayers, C. J. _et al._ Correlation between crystal purity and the charge density wave in

\(1T-{\text{V}}{\text{Se}}_{2}\). _Phys. Rev. Materials_ 4, 025002. https://doi.org/10.1103/PhysRevMaterials.4.025002 (2020). Article  ADS  CAS  Google Scholar  * DiMasi, E., Aronson, M. C.,

Mansfield, J. F., Foran, B. & Lee, S. Chemical pressure and charge-density waves in rare-earth tritellurides. _Phys. Rev. B_ 52, 14516. https://doi.org/10.1103/PhysRevB.52.14516 (1995).

Article  ADS  CAS  Google Scholar  * Laverock, J. _et al._ Fermi surface nesting and charge-density wave formation in rare-earth tritellurides. _Phys. Rev. B_ 71, 085114.

https://doi.org/10.1103/PhysRevB.71.085114 (2005). Article  ADS  CAS  Google Scholar  * Malliakas, C., Billinge, S. J. L., Kim, H. J. & Kanatzidis, M. G. Square nets of tellurium:

Rare-earth dependent variation in the charge-density wave of \(RE\text{Te}_3\) (\(RE\) = rare-earth element). _J. Am. Chem. Soc._ 127, 6510. https://doi.org/10.1021/ja0505292 (2005). Article

  CAS  PubMed  Google Scholar  * Malliakas, C. & Kanatzidis, M. G. Divergence in the behavior of the charge density wave in \(RE\text{Te}_3\) (\(RE\) = Rare-Earth Element) with

temperature and \(RE\) element. _J. Am. Chem. Soc._ 128, 12612. https://doi.org/10.1021/ja0641608 (2006). Article  CAS  PubMed  Google Scholar  * Yumigeta, K. _et al._ Advances in rare-earth

tritelluride quantum materials: Structure, properties, and synthesis. _Adv. Sci._ 8, 2004762. https://doi.org/10.1002/advs.202004762 (2021). Article  CAS  Google Scholar  * Ru, N. _et al._

Effect of chemical pressure on the charge density wave transition in rare-earth tritellurides \(R{\text{Te}}_{3}\). _Phys. Rev. B_ 77, 035114. https://doi.org/10.1103/PhysRevB.77.035114

(2008). Article  ADS  CAS  Google Scholar  * Banerjee, A. _et al._ Charge transfer and multiple density waves in the rare earth tellurides. _Phys. Rev. B_ 87, 155131.

https://doi.org/10.1103/PhysRevB.87.155131 (2013). Article  ADS  CAS  Google Scholar  * Iyeiri, Y., Okumura, T., Michioka, C. & Suzuki, K. Magnetic properties of rare-earth metal

tritellurides \(R\text{Te}_3\) (\(R = \text{ Ce, } \text{ Pr, } \text{ Nd, } \text{ Gd, } \text{ Dy }\)). _Phys. Rev. B_ 67, 144417. https://doi.org/10.1103/PhysRevB.67.144417 (2003).

Article  ADS  CAS  Google Scholar  * Ru, N., Chu, J. H. & Fisher, I. R. Magnetic properties of the charge density wave compounds \(R{\text{Te}}_{3}\) (\(R=\text{ Y}\), \(\text{ La}\),

\(\text{ Ce}\), \(\text{ Pr}\), \(\text{ Nd}\), \(\text{ Sm}\), \(\text{ Gd}\), \(\text{ Tb}\), \(\text{ Dy}\), \(\text{ Ho}\), \(\text{ Er}\), and \(\text{ Tm}\)). _Phys. Rev. B_ 78,

012410. https://doi.org/10.1103/PhysRevB.78.012410 (2008). Article  ADS  CAS  Google Scholar  * Chen, Y. _et al._ Raman spectra and dimensional effect on the charge density wave transition

in \(\text{Gd}\text{Te}_3\). _Appl. Phys. Lett._ 115, 151905. https://doi.org/10.1063/1.5118870 (2019). Article  ADS  CAS  Google Scholar  * Lei, S. _et al._ High mobility in a van der Waals

layered antiferromagnetic metal. _Sci. Adv._ 6, aay6407. https://doi.org/10.1126/sciadv.aay6407 (2020). Article  ADS  CAS  Google Scholar  * Kogar, A. _et al._ Light-induced charge density

wave in \(\text{La}\text{Te}_3\). _Nat. Phys._ 16, 159. https://doi.org/10.1038/s41567-019-0705-3 (2020). Article  CAS  Google Scholar  * Watanabe, M. _et al._ Shubnikov-de-Haas oscillation

and possible modification of effective mass in \(\text{Ce}\text{Te}_3\) thin films. _AIP Adv._ 11, 015005. https://doi.org/10.1063/9.0000074 (2021). Article  ADS  CAS  Google Scholar  *

Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. _Rev. Mod. Phys._ 75, 473. https://doi.org/10.1103/RevModPhys.75.473

(2003). Article  ADS  CAS  Google Scholar  * Damascelli, A. Probing the electronic structure of complex systems by ARPES. _Phys. Scr._ 2004, 61.

https://doi.org/10.1238/Physica.Topical.109a00061 (2004). Article  Google Scholar  * Brouet, V. _et al._ Fermi surface reconstruction in the CDW state of \({\text{Ce}\text{Te}}_{3}\)

observed by photoemission. _Phys. Rev. Lett._ 93, 126405. https://doi.org/10.1103/PhysRevLett.93.126405 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Komoda, H. _et al._

High-resolution angle-resolved photoemission study of incommensurate charge-density-wave compound \(\text{Ce}{\text{Te}}_{3}\). _Phys. Rev. B_ 70, 195101.

https://doi.org/10.1103/PhysRevB.70.195101 (2004). Article  ADS  CAS  Google Scholar  * Brouet, V. _et al._ Angle-resolved photoemission study of the evolution of band structure and charge

density wave properties in \(R{\text{Te}}_{3}\) (\(R= {\text{ Y}}\), \(\text{ La}\), \(\text{ Ce}\), \(\text{ Sm}\), \(\text{ Gd}\), \(\text{ Tb}\), and \(\text{ Dy}\)). _Phys. Rev. B_ 77,

235104. https://doi.org/10.1103/PhysRevB.77.235104 (2008). Article  ADS  CAS  Google Scholar  * Schmitt, F. _et al._ Transient electronic structure and melting of a charge density wave in

\(\text{Tb}\text{Te}_3\). _Science_ 321, 1649. https://doi.org/10.1126/science.1160778 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Moore, R. G. _et al._ Fermi surface evolution

across multiple charge density wave transitions in \(\text{Er}\text{Te}_{3}\). _Phys. Rev. B_ 81, 073102. https://doi.org/10.1103/PhysRevB.81.073102 (2010). Article  ADS  CAS  Google Scholar

  * Lou, R. _et al._ Interplay between multiple charge-density waves and the relationship with superconductivity in \({\text{Pd}}_{x}{\text{Ho}}{\text{Te}}_{3}\). _Phys. Rev. B_ 93, 115133.

https://doi.org/10.1103/PhysRevB.93.115133 (2016). Article  ADS  Google Scholar  * Lee, E. _et al._ The \(7\times 1\) fermi surface reconstruction in a two-dimensional _f _-electron charge

density wave system: \(\text{Pr}\text{Te}_3\). _Sci. Rep._ 6, 30318. https://doi.org/10.1038/srep30318 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Liu, J. S. _et

al._ Electronic structure of the high-mobility two-dimensional antiferromagnetic metal \(\text{Gd}{\text{Te}}_{3}\). _Phys. Rev. Materials_ 4, 114005.

https://doi.org/10.1103/PhysRevMaterials.4.114005 (2020). Article  ADS  CAS  Google Scholar  * Seong, S. _et al._ Angle-resolved photoemission spectroscopy study of a system with a double

charge density wave transition: \({\text{ErTe}}_{3}\). _Phys. Rev. B_ 104, 195153. https://doi.org/10.1103/PhysRevB.104.195153 (2021). Article  ADS  CAS  Google Scholar  * Chikina, A. _et

al._ Charge density wave generated Fermi surfaces in \(\text{Nd}\text{Te}_3\). _Phys. Rev. B_ 107, L161103. https://doi.org/10.1103/PhysRevB.107.L161103 (2023). Article  ADS  CAS  Google

Scholar  * Zocco, D. A. _et al._ Pressure dependence of the charge-density-wave and superconducting states in \({\text{Gd}}{\text{Te}}_{3}, {\text{Tb}}{\text{Te}}_{3}\), and

\({\text{DyTe}}_{3}\). _Phys. Rev. B_ 91, 205114. https://doi.org/10.1103/PhysRevB.91.205114 (2015). Article  ADS  CAS  Google Scholar  * Guo, Q., Bao, D., Zhao, L. J. & Ebisu, S. Novel

magnetic behavior of antiferromagnetic \(\text{Gd}\text{Te}_3\) induced by magnetic field. _Phys. B: Condens. Matter_ 617, 413153. https://doi.org/10.1016/j.physb.2021.413153 (2021). Article

  CAS  Google Scholar  * Fang, A., Ru, N., Fisher, I. R. & Kapitulnik, A. STM studies of \(\text{Tb}\text{Te}_3\): Evidence for a fully incommensurate charge density wave. _Phys. Rev.

Lett._ 99, 046401. https://doi.org/10.1103/PhysRevLett.99.046401 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Wang, Y. _et al._ Axial Higgs mode detected by quantum pathway

interference in \(R\text{Te}_3\). _Nature_ 606, 896. https://doi.org/10.1038/s41586-022-04746-6 (2022). Article  ADS  CAS  PubMed  Google Scholar  * Ru, N. & Fisher, I. R. Thermodynamic

and transport properties of \(\text{Y}{\text{Te}}_{3}, \text{La}{\text{Te}}_{3}\), and \(\text{Ce}{\text{Te}}_{3}\). _Phys. Rev. B_ 73, 033101. https://doi.org/10.1103/PhysRevB.73.033101

(2006). Article  ADS  CAS  Google Scholar  * Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. _Phys. Rev._ 136, B864. https://doi.org/10.1103/PhysRev.136.B864 (1964). Article  ADS 

MathSciNet  Google Scholar  * Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. _Phys. Rev._ 140, A1133.

https://doi.org/10.1103/PhysRev.140.A1133 (1965). Article  ADS  MathSciNet  Google Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953.

https://doi.org/10.1103/PhysRevB.50.17953 (1994). Article  ADS  Google Scholar  * Giannozzi, P. _et al._ Quantum ESPRESSO: A modular and open-source software project for quantum simulations

of materials. _J. Phys. Condens. Matter_ 21, 395502. https://doi.org/10.1088/0953-8984/21/39/395502 (2009). Article  PubMed  Google Scholar  * Giannozzi, P. _et al._ Advanced capabilities

for materials modelling with quantum ESPRESSO. _J. Phys. Condens. Matter_ 29, 465901. https://doi.org/10.1088/1361-648X/aa8f79 (2017). Article  CAS  PubMed  Google Scholar  * Giannozzi, P.

_et al._ Quantum ESPRESSO toward the exascale. _J. Chem. Phys._ 152, 154105. https://doi.org/10.1063/5.0005082 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Perdew, J. P., Burke, K.

& Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865. https://doi.org/10.1103/PhysRevLett.77.3865 (1996). Article  ADS  CAS  PubMed  Google Scholar

  * Dal Corso, A. Pseudopotentials periodic table: From H to Pu. _Comput. Mater. Sci._ 95, 337. https://doi.org/10.1016/j.commatsci.2014.07.043 (2014). Article  CAS  Google Scholar  *

Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. _Phys. Rev. B_ 13, 5188. https://doi.org/10.1103/PhysRevB.13.5188 (1976). Article  ADS  MathSciNet  Google

Scholar  * Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. _Phys. Rev. B_ 56, 12847. https://doi.org/10.1103/PhysRevB.56.12847

(1997). Article  ADS  CAS  Google Scholar  * Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. _Phys. Rev. B_ 65, 035109.

https://doi.org/10.1103/PhysRevB.65.035109 (2001). Article  ADS  CAS  Google Scholar  * Pizzi, G. _et al._ Wannier90 as a community code: new features and applications. _J. Phys. Condens.

Matter_ 32, 165902. https://doi.org/10.1088/1361-648X/ab51ff (2020). Article  ADS  CAS  PubMed  Google Scholar  * Sancho, M. P. L.,  Sancho, J. M. L., Sancho, J. M. L. & Rubio, J. Highly

convergent schemes for the calculation of bulk and surface Green functions, _J. Phys. F: Met. Phys._ 15, 851. https://doi.org/10.1088/0305-4608/15/4/009 (1985). * Wu, Q., Zhang, S., Song,

H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: An open-source software package for novel topological materials, _Comput. Phys. Commun._ 224, 405.

https://doi.org/10.1016/j.cpc.2017.09.033 (2018). Download references ACKNOWLEDGEMENTS M.N. acknowledges the support from the National Science Foundation (NSF) CAREER award DMR-1847962, the

NSF Partnerships for Research and Education in Materials (PREM) Grant DMR-2121953, and the Air Force Office of Scientific Research MURI Grant No. FA9550-20-1-0322. D.K. was supported by the

National Science Centre (Poland) under research grant 2021/41/B/ST3/01141. A.P. acknowledges the support by National Science Centre (NCN, Poland) under Projects No. 2021/43/B/ST3/02166 and

also appreciates the funding in the frame of scholarships of the Minister of Science and Higher Education (Poland) for outstanding young scientists (2019 edition, No. 818/STYP/14/2019).

S.I.K. acknowledges the support from the NSF PREM Grant DMR-2121953. The use of SSRL in SLAC National Accelerator Laboratory is supported by the U.S. Department of Energy (DOE), Office of

Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. This research also used the resources of the Advanced Light Source (ALS), which is a DOE Office of Science User

Facility under contract no. DE-AC02-05CH11231. We are grateful to Makoto Hashimoto & Donghui Lu at SSRL and Alexei Fedorov & Sung-Kwan Mo at ALS for the beamline assistance. AUTHOR

INFORMATION Author notes * Sabin Regmi Present address: Center for Quantum Actinide Science and Technology, Idaho National laboratory, Idaho Falls, ID, 83415, USA AUTHORS AND AFFILIATIONS *

Department of Physics, University of Central Florida, Orlando, FL, 32816, USA Sabin Regmi, Iftakhar Bin Elius, Anup Pradhan Sakhya, Dylan Jeff, Milo Sprague, Mazharul Islam Mondal, Damani

Jarrett, Nathan Valadez, Alexis Agosto, Saiful I. Khondaker & Madhab Neupane * NanoScience Technology Center, University of Central Florida, Orlando, FL, 32826, USA Dylan Jeff & 

Saiful I. Khondaker * Institute of Low Temperature and Structure Research, Polish Academy of Sciences, Okólna 2, 50-422, Wrocław, Poland Tetiana Romanova & Dariusz Kaczorowski *

Department of Physics, University of Washington, Seattle, WA, 98195, USA Jiun-Haw Chu * Institute of Nuclear Physics, Polish Academy of Sciences, W. E. Radzikowskiego 152, 31342, Kraków,

Poland Andrzej Ptok Authors * Sabin Regmi View author publications You can also search for this author inPubMed Google Scholar * Iftakhar Bin Elius View author publications You can also

search for this author inPubMed Google Scholar * Anup Pradhan Sakhya View author publications You can also search for this author inPubMed Google Scholar * Dylan Jeff View author

publications You can also search for this author inPubMed Google Scholar * Milo Sprague View author publications You can also search for this author inPubMed Google Scholar * Mazharul Islam

Mondal View author publications You can also search for this author inPubMed Google Scholar * Damani Jarrett View author publications You can also search for this author inPubMed Google

Scholar * Nathan Valadez View author publications You can also search for this author inPubMed Google Scholar * Alexis Agosto View author publications You can also search for this author

inPubMed Google Scholar * Tetiana Romanova View author publications You can also search for this author inPubMed Google Scholar * Jiun-Haw Chu View author publications You can also search

for this author inPubMed Google Scholar * Saiful I. Khondaker View author publications You can also search for this author inPubMed Google Scholar * Andrzej Ptok View author publications You

can also search for this author inPubMed Google Scholar * Dariusz Kaczorowski View author publications You can also search for this author inPubMed Google Scholar * Madhab Neupane View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS M.N. conceived the study; D.K. & T.R. synthesized the single-crystals and performed the bulk

properties measurements; S.R. performed the ARPES measurements with the help of A.P.S., I.B.E., M.S., M.I.M., D.J., N.V. & A.A.; A.P. performed the  first-principles calculations; S.K.

& D.J. carried out the Raman measurements with the help of & J.-H.C. ; S.R. analyzed the data; S.R. & M.N. made the figure plan and manuscript was prepared with contributions

from all the authors. CORRESPONDING AUTHOR Correspondence to Madhab Neupane. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION

PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Regmi, S., Bin Elius, I., Sakhya, A. _et al._ Observation of momentum-dependent charge density wave gap in a layered antiferromagnet \({\textrm{Gd}}{\textrm{Te}}_{3}\). _Sci Rep_

13, 18618 (2023). https://doi.org/10.1038/s41598-023-44851-8 Download citation * Received: 14 June 2023 * Accepted: 12 October 2023 * Published: 30 October 2023 * DOI:

https://doi.org/10.1038/s41598-023-44851-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative