News Reader.info

ABSTRACT We propose a sparse computation method for optimizing the inference of neural networks in reinforcement learning (RL) tasks. Motivated by the processing abilities of the brain, this

method combines simple neural network pruning with a delta-network algorithm to account for the input data correlations. The former mimics neuroplasticity by eliminating inefficient

connections; the latter makes it possible to update neuron states only when their changes exceed a certain threshold. This combination significantly reduces the number of multiplications

during the neural network inference for fast neuromorphic computing. We tested the approach in popular deep RL tasks, yielding up to a 100-fold reduction in the number of required

multiplications without substantial performance loss (sometimes, the performance even improved). SIMILAR CONTENT BEING VIEWED BY OTHERS NEURAL NETWORK COMPRESSION FOR REINFORCEMENT LEARNING

TASKS Article Open access 21 March 2025 DISCOVERING FASTER MATRIX MULTIPLICATION ALGORITHMS WITH REINFORCEMENT LEARNING Article Open access 05 October 2022 DEEP NEURAL NETWORKS USING A

SINGLE NEURON: FOLDED-IN-TIME ARCHITECTURE USING FEEDBACK-MODULATED DELAY LOOPS Article Open access 27 August 2021 INTRODUCTION Modern deep learning (DL) gravitates towards large neural

networks, with ever-increasing demands for computational resources to perform basic arithmetic operations, such as multiplication. When used with contemporary DL hardware, known to face the

limitation of the von Neumann bottleneck1, this results in a substantial energy consumption and significant delays during the network inference. At the same time, the human brain is capable

of inferring with remarkable efficiency by dismissing the irrelevant signals and connections, consuming just 10–20 W for basic cognitive tasks2. Such efficiency motivated our study to

optimize the DL inference by taking into account _only significant_ signals. Specifically, we consider the inference in RL tasks, using the popular Atari games environment3 as the sandbox.

In the brain, the presence of regular dense layers is not evident. Instead, the brain employs neural rewiring as a means to eliminate inefficient and unnecessary connections4. At the same

time, recent studies5,6,7 demonstrate that in many cases significant part of neural connections are excessive and can be removed without a drop in the neural network’s predictive power (or

with a negligible one). The optimization technique, known as pruning, represents a method to attain structural sparsity within a neural network. The conceptualization of this approach can be

traced back to the 1990s8,9. Today, there are multiple strategies for identifying redundant connections within neural networks, including the examination of absolute values, the Hessian

matrix, decomposition methods, and others5,10. Moreover, neural networks often anticipate the input data in a form of sequential highly correlated signals or frames, as observed in domains

like video, audio, monitoring and control problems, including RL. In such tasks, the information processed by a neural network at time step _t_ closely resembles what it analyzed at the time

step \(t-1\). This phenomenon is referred to as temporal sparsity, also characteristic of the perceptual systems in the brain4,11. Some studies propose various optimization algorithms for

neural networks handling such temporal sparse data12,13,14,15. These approaches are based on the idea of asynchronous updates, where only the states of neurons that have changed

significantly, compared to the previous step, are updated. It is worth noting that the brain neurons also operate asynchronously, transmitting signals to each other only when necessary. A

typical neural network layer could be represented as a matrix-vector multiplication combined with the application of a nonlinear transformation. Therefore, for the input vector _x_, the

\(j^{\text {th}}\) value of the output vector _y_ could be represented as $$\begin{aligned} y^j = f(w_1^j * x_1 + \dots + w_n^j * x_n), \end{aligned}$$ where _f_ is a nonlinear function

applied to the Multiply and Accumulate (MAC) operation. The MAC operation is the summation of products of the input vector elements and the respective weights _w_. If at least one operand in

any of such multiplications is zero, then such multiplication could be omitted. In this work, we refer to a multiplication of two numbers as _significant_ if neither operand is equal to

zero. In this study, we propose a combination of the two aforementioned approaches to optimize the inference of Neural Networks in RL tasks with the video inputs. More specifically, we

optimize the inference of a popular DQN algorithm16 for the Atari games. The pruning approach yields a 2–8\(\times \) reduction in the number of significant neural network multiplications.

The second part of our approach achieves a further 10–50-fold reduction. When combined, these approaches result in a 20–100-fold reduction in the number of significant multiplications,

without notable performance loss and in some cases, even enhancing the original performance. The proposed combination of these methods is biologically inspired and exhibits neuromorphic

properties for fast information processing1. To the best of our knowledge, such an approach has never been applied in deep RL problems. BACKGROUND DEEP Q-NETWORK In RL tasks17, an agent

receives the current environment state _s_ as an input, after which it selects action _a_, and then it goes to a new state \(s'\), and it receives a certain reward _r_. The agent’s goal

is to maximize the total reward. More strictly, the environment is formalized as a Markov decision process. A Markov decision process (MDP) is a tuple (_S_, _A_, _P_, _R_), where _S_ is a

set of possible states and _A_ is a set of possible actions. _P_ is the function describing transition between states; \(P_{a}(s, s') = Pr(s_{t+1} = s' | s_t = s, a_t = a)\), i.e.,

the probability to get into state \(s'\) at the next step when selecting action _a_ in state _s_. \(R = R_{a}(s,s')\) is the function describing receiving rewards. It determines

how big a reward an agent will receive when transitioning from state _s_ to state \(s'\) by selecting action _a_. The strategy an agent uses to select its actions _a_ depending on state

_s_ is called a policy and is usually denoted by the letter \(\pi _\theta \) where \(\theta \) denotes policy parameters. One way to solve an RL task is _Q_-function-based approaches. A

_Q_-function has two parameters - _s_ and _a_. \(Q_{\pi _\theta }(s,a)\) estimates what cumulative reward the agent following policy \({\pi _\theta }\) will receive if it performs action _a_

from state _s_ and then follows policy \({\pi _\theta }\). If complete information about an environment is available, the exact value of a _Q_-function can be calculated. However, the

knowledge of the world is usually incomplete and the number of possible states is enormous. Therefore, the _Q_-function can be approximated using neural networks. This approach named DQN

(Deep Q-Network) was demonstrated by DeepMind in16. In the present study, we use this algorithm to train Neural Networks for Atari RL tasks. PRUNING AND LOTTERY TICKET HYPOTHESIS The authors

of7 have proposed the Lottery Ticket Hypothesis. The hypothesis states that when at any stage of neural network training the smallest weights by absolute value are pruned (set to zero and

frozen) and the remaining weights are reset to the values they had before the training, and then neural network training is resumed, the training capabilities of such neural network will

remain the same. However, this does not happen if we set the remaining weights to random (not initial) values. Furthermore, the investigation reveals that sparse neural networks, which have

undergone such pruning and training, can exhibit superior performance compared to unpruned neural networks. In practice7,18,19 neural network iterative magnitude pruning by absolute value is

usually used. This approach involves training neural networks, followed by pruning a small percentage of their weights (typically 10-20%). The remaining weights are then reset to their

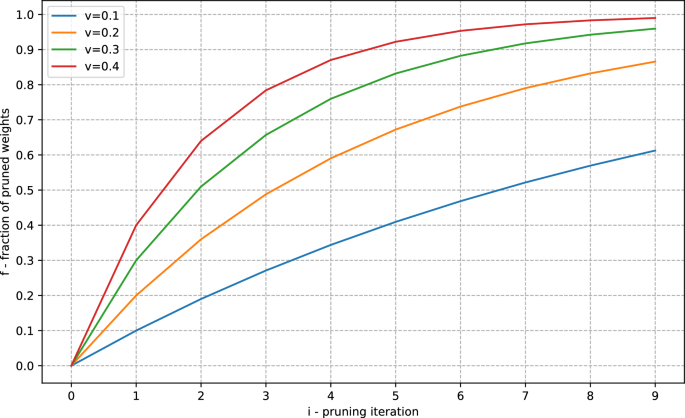
initial values, and this process is repeated for a specified number of iterations, denoted as _M_. Consequently, given a pruning rate of _v_, the fraction _f_ of pruned weights can be

computed as follows: $$\begin{aligned} f = \frac{pruned\_weights}{total\_weights} = 1 - (1-v)^i,\quad i \in [0:M) \end{aligned}$$ (1) where _i_ is the pruning iteration. Figure 1 displays

the relationships between the fraction of pruned weights and various values of _i_ and _v_. In18,19 it was shown that the phenomenon of the Lottery Ticket Hypothesis is observed in RL tasks

as well. In particular, the authors of19 investigated this phenomenon within the context of the DQN algorithm. DELTANETWORK ALGORITHM The output values of the neural network layer number

\(k+1\) can be written as: $$\begin{aligned} o^{k+1}= & {} W^{k} x^{k} + b^{k} \end{aligned}$$ (2) $$\begin{aligned} x^{k+1}= & {} f(o^{k+1}) \end{aligned}$$ (3) where \(x^{k+1} \in

R^n\) is the output of \(k+1\) neural network layer, \(x^k \in R^n\) is the input of \(k+1\) neural network layer (output of _k_ layer), \(W^{k} \in R^{nxn}\) is the weight matrix, and

\(b^{k} \in R^{n}\) is the bias. In a conventional neural network, for every new input vector \(x^{k}(t)\) in the moment of time t a total recomputation of output value \(x^{k+1}(t)\) is

required, which will require \(n^2\) multiplications. However, the following should be noted: $$\begin{aligned} \Delta x^k(t)= & {} x^k(t) - x^k(t-1) \end{aligned}$$ (4)

$$\begin{aligned} o^{k+1}(t)= & {} W^{k} \Delta x^{k}(t) + o^{k+1}(t-1) \end{aligned}$$ (5) $$\begin{aligned} \Delta x^{k+1}(t)= & {} f(o^{k+1}(t)) - f(o^{k+1}(t-1)) \end{aligned}$$

(6) Thus, it is possible to recompute layer output values at the moment of time t using Eqs. (4), (5), (6) using layer input changes that occur relative to the state at the moment \(t-1\).

This remark does not lead to neural network optimization by itself. But we can introduce threshold _T_ for output value changes \(\Delta x^{k}(t)\) such that recomputation of succeeding

neurons is started only when an output value exceeds this threshold. Authors of12,13 call this approach “Hysteresis Quantizer”. To implement it, it is necessary to introduce an additional

variable \(x\_prev(t)\) into each neuron. Such a variable will be used to record the last transmitted value. Thus, the following Algorithm 1 will be run on each neuron: RELATED WORKS To the

best of our knowledge, we present the first attempt to combine the temporal and the structural sparsity for optimizing inference in RL tasks. However, there are several publications that

applied pruning18,20 and other optimization techniques to RL problems, e.g., distillation21. Also, there are works that employ the DeltaNetwork algorithm for convolutional and recurrent

neural networks13,22,23. METHODS In the previous section, we described two neural network optimization algorithms: Pruning and DeltaNetwork Algorithm. The following neural network

optimization becomes possible when these approaches are applied jointly: STAGE 1—TRAINING: * 1. Train neural network in the environment * 2. Prune (set to zero and freeze) lowest \(v = 20\)%

weights * 3. Reset remaining weights to original * 4. Train neural network again in the environment * 5. Repeat steps 2–4 \(M = 10\) times Using this algorithm, we obtain a set of

structurally sparse neural networks with different degrees of sparsity. The number of neural networks in the set equals the number of pruning algorithm iterations. The general scheme of the

learning stage of the algorithm is shown in Fig. 2. STAGE 2—INFERENCE: Then we apply the DeltaNetwork Algorithm with the threshold \(T = 0.01\) to the inference of the trained neural

networks. As a result, we get a set of new neural networks using both structure and temporal sparsity. The selection of one neural network from such a set depends on the desirable balance

between the number of significant multiplications and neural network performance. The scheme of the inference stage is presented in Fig. 3. EXPERIMENTS NEURAL NETWORK ARCHITECTURE In this

study, we conducted all experiments using the following Neural Network architecture. An 84 \(\times \) 84 \(\times \) 4 matrix received from the environment is an input to the neural

network, which consists of 4 sequential game frames. The first convolutional layer consists of 32 8 \(\times \) 8 filters with strides equal to 4 and ReLU activations. The second layer

consists of 32 4 \(\times \) 4 filters with strides equal to 2 and ReLU activations. The third layer consists of 64 3 \(\times \) 3 filters with strides equal to 2 and ReLU activations. They

are followed by a dense layer with 512 neurons with ReLU activations. At the output there is another dense layer with a number of neurons equal to the number of actions in a video game.

Depending on the video game, the number of actions _n_ may vary from 4 to 18. The neural network structure is shown in Fig. 4. RL ENVIRONMENTS We experimented within the following RL

environments: Breakout, SpaceInvaders, Robotank, Enduro, Krull and Freeway. Figure 5 shows frames from these video games. For example, in Breakout, an agent has to hit as many bricks as

possible by hitting the ball. In Spacelnvaders, an agent has to eliminate all alien spaceships. SIGNIFICANT OPERATIONS COUNTING THE NUMBER OF MULTIPLICATIONS BEFORE OPTIMIZATION Let us

estimate the number of multiplications in a standard neural network without any optimizations. The following formula can be used to estimate the number of multiplications in a convolutional

layer _k_: $$\begin{aligned} {\gamma _k} = size\_x_{k+1} * size\_y_{k+1} * {filters_{k+1}}* kernel\_size\_x_{k} * kernel\_size\_y_{k} * filters_{k}, \end{aligned}$$ (7) where *

\(size\_x_{k+1}\)—is the \(k+1\) layer input size along the _x_ axis * \(size\_y_{k+1}\)—is the \(k+1\) layer input size along the _y_ axis * \(filters_{k+1}\)—is the number of filters at

layer _k_ (\(k+1\) layer input size along the _z_ axis) * \(kernel\_size\_x_{k}\)—is the convolution size along the _x_ axis * \(kernel\_size\_y_{k}\)—is the convolution size along the _y_

axis * \(filters_{k}\)—is the _k_ layer input size along the _z_ axis The following formula can be used to count multiplications in dense layer _k_: $$\begin{aligned} {\gamma _k} = input_{k}

* output_{k}, \end{aligned}$$ (8) where * \(input_{k}\)—is the _k_ layer input size (number of neurons at \(k-1\) layer) * \(output_{k}\)—is the _k_ layer output size (number of neurons at

_k_ layer) General results for all layers are presented in Table 1. It should be noted that these results are universal for any Atari environment and for any DQN run. THE NUMBER OF

MULTIPLICATIONS AFTER OPTIMIZATION It is clear that the degree of weight sparsity will affect the number of non-zero multiplications. However, the delta algorithm provides different levels

of temporal sparsity depending on the selected threshold, layer, and input data. That is why it is impossible to analytically estimate the number of non-zero multiplications. Therefore we

empirically calculated the number of significant multiplications by calculating all operations that have zero operands. Examples of the numbers of significant multiplications are given in

the next section and in Tables 2 and 3. RESULTS Figure 6 shows the abovementioned neural network performance metrics at different sparsity levels and for different environments. The reward

metric results (blue line) are similar to the results from18,19, where the highest decrease of reward during pruning was in SpaceInvaders and Breakout. In these environments performance

dropped very quickly as neural network sparsity grew. At the same time for Enduro the reward during the pruning does not decrease. It even increases. For Robotank and Freeway the performance

does not degrade seriously, and even for some sparsity levels it increases in comparison with the unpruned version. Thus it is possible to use very sparse neural networks for some

environments without the loss of performance. The orange line demonstrates the rewards for the neural networks with delta neurons. We can see that they have similar (sometimes a little bit

higher, sometimes a little bit lower) performance to a network without delta neurons. This means that the delta algorithm does not influence the reward gravely. The gain in the number of

non-zero multiplications (black dotted line) is dependent on the game the agent is playing. For example, in SpaceInvaders the fraction of the non-zero multiplications is in the range from

0.065 to 0.022. At the same time in Breakout this value is in the range from 0.018 to 0.009. The delta algorithm alone (without the weight pruning) leads to a decreasing in the number of

non-zero multiplication operations from 5.5 times for Robotank to 55 times for Breakout. At the same time, the pruning leads to a more modest gain. For some environments, the fraction of

non-zero multiplication operations decreases as a result of pruning more than for others. E.g., for Robotank the fraction of non-zero multiplication operations decrease during pruning from

0.184 to 0.059 (about x3.11). At the same time for Breakout it decreases only from 0.018 to 0.015 (x1.2). Anyway, it is clear that the gain of the delta algorithm is much higher than the

gain of the pruning. Moreover, pruning sometimes leads to the degradation of performance. We made 5 runs for every environment and averaged all metrics presented here. In the Supplementary

Materials, the tables with the number of non-zero multiplication operations in layers are shown for each tested environment. In these tables, one can see that the highest gains occur in the

first layers. DISCUSSION The variety in performance gain between different environments can be explained by the fact that some environments (e.g., SpaceInvaders) have much more changing

pixels at each time step than others (e.g., Breakout). In the Breakout only the playground and the ball move, while in the SpaceInvaders several objects can move at once—shots, a ship and

aliens. This is well confirmed by the difference in delta sparsity (the fraction of neuron activations during the delta algorithm execution) level when playing Breakout and SpaceInvaders

(see Tables 2 and 3). In Fig. 7, we visualized the correlation between the level of input sparsity caused by the delta algorithm with the fraction of zero multiplications. We see a tendency

for the fraction of zero multiplications to increase during inference with an increase in the fraction of input zeros. Both parts of the optimization approach (pruning and delta algorithm)

presented here contribute to the reduction of the number of significant multiplications (see Fig. 6). Thus here we provided an efficient combination of structural and temporal sparsity.

Furthermore, we conducted an examination of how the parameter _T_ (threshold) affects the performance and the operational gains. We assessed the performance in both Krull and SpaceInvaders

using various values of _T_, namely 0.001, 0.005, 0.01, and 0.05. The results are presented in Fig. 8, clearly illustrating that 0.01 is the most favorable parameter value among those

tested. The higher values, despite winning in the multiplication options, result in a significant decrease in the rewards. Whereas, the lower thresholds yield nearly identical rewards, with

a more modest productivity improvement. Multiplication is an expensive computational operation from the point of view of energy and time24. The desire to reduce the number of these

operations is obvious. The provided algorithm decreases the number of significant multiplications. Moreover, due to the structural sparsity, this approach reduces the number of memory

accesses, that are also very expensive in energy and time24. However, presently, there are very few opportunities to use the existing hardware to effectively implement this algorithm. This

is due to modern GPUs being designed for handling dense matrices. Nevertheless, there are attempts to turn the situation. Nvidia began offering hardware support of sparse matrix operations

on one of its Tesla A100 GPUs; however, the maximum supported sparsity is only 75% so far25. The authors of the abovementioned DeltaNetwork algorithm introduced the NeuronFlow26,27

architecture that supports delta algorithm. The Loihi2 processor that Intel presented28 in September 2021 also has the multi-core asynchronous architecture capable of running sparse delta

neuron-based neural networks. In18, it was shown that the Lottery Ticket Hypothesis pruning approach also works for RL algorithms trained by the A2C method. At the same time, DeltaNetwork

Algorithm could be applied to any network working with sequential data. Thus, the RL algorithm for neural network training is not restricted by DQN. In the future, it would be highly

interesting to apply the proposed algorithm in new environments and real-world control tasks, assessing its performance on real hardware to measure the real efficiency gain. Additionally, it

would be worthwhile to explore the potential enhancement of this algorithm through the incorporation of other neural network optimization methods, such as quantization, which can lead to

reduced memory footprint and integer arithmetic. CONCLUSION This study demonstrates the large redundancy of the operation of multiplication during the inference of neural networks in popular

RL tasks. Minimizing the number of multiplications will prove critical in the areas where computational and energy efficiency are key, for example Edge AI29, real-time control30,

robotics31,32,33, and many others. While suitable equipment to take full advantage of these benefits is currently not available to a consumer, the computational chips capable of evaluating

the network inference in the proposed way are currently being researched and developed as a part of neuromorphic computing paradigm. Our study highlights the importance of significant

multiplications inference for a plethora of such neuromorphic computing applications. DATA AVAILABILITY The data generated or analysed during this study are included in this article and its

supplementary information files. Supplementary Tables summarizes the numerical results in all game environments. Supplementary Information 2 contains a model and its neural network weights

for the Enduro game (the other weights are available upon request). Supplementary Information 1 contains the source code for the sparse model inference. REFERENCES * Ivanov, D., Chezhegov,

A., Kiselev, M., Grunin, A. & Larionov, D. Neuromorphic artificial intelligence systems. _Frontiers in Neuroscience_ 16 (2022). * Attwell, D. & Laughlin, S. B. An energy budget for

signaling in the grey matter of the brain. _Journal of Cerebral Blood Flow & Metabolism_ 21, 1133–1145 (2001). Article  CAS  Google Scholar  * Bellemare, M., Veness, J. & Bowling, M.

Investigating contingency awareness using atari 2600 games. _In Proceedings of the AAAI Conference on Artificial Intelligence_ 26, 864–871 (2012). Article  Google Scholar  * Hudspeth, A.

J., Jessell, T. M., Kandel, E. R., Schwartz, J. H. & Siegelbaum, S. A. _Principles of neural science_ (McGraw-Hill, Health Professions Division, 2013). Google Scholar  * Blalock, D.,

Ortiz, J. J. G., Frankle, J. & Guttag, J. What is the state of neural network pruning? arXiv preprint arXiv:2003.03033 (2020). * Gomez, A. N. _et al._ Learning sparse networks using

targeted dropout. arXiv preprint arXiv:1905.13678 (2019). * Frankle, J. & Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. arXiv preprint

arXiv:1803.03635 (2018). * LeCun, Y., Denker, J. S. & Solla, S. A. Optimal brain damage. In _Advances in Neural Information Processing Systems_, 598–605 (1990). * Hassibi, B. &

Stork, D. G. _Second Order Derivatives for Network Pruning: Optimal Brain Surgeon_ (Morgan Kaufmann, 1993). Google Scholar  * Liang, T., Glossner, J., Wang, L., Shi, S. & Zhang, X.

Pruning and quantization for deep neural network acceleration: A survey. _Neurocomputing_ 461, 370–403 (2021). Article  Google Scholar  * Krylov, D., Dylov, D. V. & Rosenblum, M.

Reinforcement learning for suppression of collective activity in oscillatory ensembles. _Chaos_ 30, 033126 (2020). https://doi.org/10.1063/1.5128909.

https://pubs.aip.org/aip/cha/article-pdf/doi/10.1063/1.5128909/14626706/033126_1_online.pdf * Yousefzadeh, A. _et al._ Asynchronous spiking neurons, the natural key to exploit temporal

sparsity. _IEEE J. Emerg. Sel. Top. Circuits Syst._ 9, 668–678 (2019). Article  ADS  Google Scholar  * Khoei, M. A., Yousefzadeh, A., Pourtaherian, A., Moreira, O. & Tapson, J. Sparnet:

Sparse asynchronous neural network execution for energy efficient inference. In _2020 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS)_, 256–260

(IEEE, 2020). * Neil, D., Lee, J. H., Delbruck, T. & Liu, S.-C. Delta networks for optimized recurrent network computation. In _International Conference on Machine Learning_, 2584–2593

(PMLR, 2017). * O’Connor, P. & Welling, M. Sigma delta quantized networks. arXiv preprint arXiv:1611.02024 (2016). * Mnih, V. _et al._ Human-level control through deep reinforcement

learning. _Nature_ 518, 529–533 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Sutton, R. S. & Barto, A. G. _Reinforcement Learning: An Introduction_ (MIT Press, 2018). MATH 

Google Scholar  * Yu, H., Edunov, S., Tian, Y. & Morcos, A. S. Playing the lottery with rewards and multiple languages: Lottery tickets in RL and NLP. arXiv preprint arXiv:1906.02768

(2019). * Vischer, M. A., Lange, R. T. & Sprekeler, H. On lottery tickets and minimal task representations in deep reinforcement learning. arXiv preprint arXiv:2105.01648 (2021). *

Graesser, L., Evci, U., Elsen, E. & Castro, P. S. The state of sparse training in deep reinforcement learning. In _International Conference on Machine Learning_, 7766–7792 (PMLR, 2022).

* Rusu, A. A. _et al._ Policy distillation. arXiv preprint arXiv:1511.06295 (2015). * Gao, C., Neil, D., Ceolini, E., Liu, S.-C. & Delbruck, T. Deltarnn: A power-efficient recurrent

neural network accelerator. In _Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays_, 21–30 (2018). * Gao, C., Delbruck, T. & Liu, S.-C. Spartus:

A 9.4 top/s FPGA-based LSTM accelerator exploiting spatio-temporal sparsity. _IEEE Transactions on Neural Networks and Learning Systems_ (2022). * Horowitz, M. 1.1 computing’s energy problem

(and what we can do about it). In _2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC)_, 10–14 (IEEE, 2014). * Krashinsky, R., Giroux, O., Jones, S.,

Stam, N. & Ramaswamy, S. Nvidia ampere architecture in-depth. NVIDIA blog: https://devblogs.nvidia.com/nvidia-ampere-architecture-in-depth (2020). * Moreira, O. _et al._ Neuronflow: A

neuromorphic processor architecture for live ai applications. In _2020 Design, Automation and Test in Europe Conference and Exhibition (DATE)_, 840–845 (IEEE, 2020). * Moreira, O. _et al._

Neuronflow: A hybrid neuromorphic-dataflow processor architecture for AI workloads. In _2020 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS)_, 01–05

(IEEE, 2020). * Intel. Taking neuromorphic computing to the next level with loihi 2. _Technology Brief_ (2021). * Singh, R. & Gill, S. S. Edge AI: A survey. _Internet Things Cyber-Phys.

Syst._ 3, 71–92 (2023). https://www.sciencedirect.com/science/article/pii/S2667345223000196 * Anikina, A., Rogov, O. Y. & Dylov, D. V. Detect to focus: Latent-space autofocusing system

with decentralized hierarchical multi-agent reinforcement learning. _IEEE Access_ (2023). * DeWolf, T., Jaworski, P. & Eliasmith, C. Nengo and low-power AI hardware for robust, embedded

neurorobotics. _Front. Neurorobotics_ 14, 568359 (2020). Article  Google Scholar  * Stagsted, R. K. _et al._ Event-based PID controller fully realized in neuromorphic hardware: a one dof

study. In _2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)_, 10939–10944 (IEEE, 2020). * Yan, Y. _et al._ Comparing Loihi with a SpiNNaker 2 prototype on

low-latency keyword spotting and adaptive robotic control. _Neuromorphic Comput. Eng._ 1, 014002 (2021). Article  Google Scholar  Download references FUNDING This study was funded by Russian

Foundation for Basic Research (No. 21-51-12012). AUTHOR INFORMATION Author notes * These authors contributed equally: Dmitry A. Ivanov and Denis A. Larionov. * These authors jointly

supervised this work: Mikhail V. Kiselev and Dmitry V. Dylov. AUTHORS AND AFFILIATIONS * Lomonosov Moscow State University, GSP-1, Leninskie Gory, Moscow, 119991, Russia Dmitry A. Ivanov *

Cifrum, 3 Kholodil’nyy per., Moscow, 115191, Russia Dmitry A. Ivanov, Denis A. Larionov & Mikhail V. Kiselev * Chuvash State University, 15 Moskovsky pr., Cheboksary, Chuvash Republic,

428015, Russia Denis A. Larionov & Mikhail V. Kiselev * Skolkovo Institute of Science and Technology, 30/1 Bolshoi blvd., Moscow, 121205, Russia Dmitry V. Dylov * Artificial Intelligence

Research Institute, 32/1 Kutuzovsky pr., Moscow, 121170, Russia Dmitry V. Dylov Authors * Dmitry A. Ivanov View author publications You can also search for this author inPubMed Google

Scholar * Denis A. Larionov View author publications You can also search for this author inPubMed Google Scholar * Mikhail V. Kiselev View author publications You can also search for this

author inPubMed Google Scholar * Dmitry V. Dylov View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.A.I., D.A.L., D.V.D. and M.V.K.

contributed to the conception and the design of the experiments. D.A.I. developed the code for experiments. D.A.I. and D.A.L. conducted experiments. D.A.I. wrote the initial draft of the

manuscript. D.A.I., D.A.L., M.V.K., and D.V.D. participated in data analysis. All authors contributed to manuscript revision, read, and approved the submitted version. CORRESPONDING AUTHOR

Correspondence to Dmitry V. Dylov. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains

neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION 1. SUPPLEMENTARY INFORMATION 2.

SUPPLEMENTARY TABLES. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation,

distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and

indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to

the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will

need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE

CITE THIS ARTICLE Ivanov, D.A., Larionov, D.A., Kiselev, M.V. _et al._ Deep reinforcement learning with significant multiplications inference. _Sci Rep_ 13, 20865 (2023).

https://doi.org/10.1038/s41598-023-47245-y Download citation * Received: 09 August 2023 * Accepted: 10 November 2023 * Published: 27 November 2023 * DOI:

https://doi.org/10.1038/s41598-023-47245-y SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative