News Reader.info

ABSTRACT Genomic prediction holds significant potential for advancing precision medicine in humans, as well as accelerating genetic improvement in animals and plants. For multi-trait

prediction, the conventional multi-trait models are primarily based on global genetic correlations between traits. With the development of local genetic correlation (LGC) estimation methods,

it is now possible to analyze LGCs confined to specific genomic regions and it is expected that incorporating LGCs into multi-trait prediction model would enhance the prediction ability.

Here, we proposed three models to address this issue and evaluated their performances using simulated data and three real datasets from human, cow, and pig populations. Our results

demonstrate that LGCs are heterogeneous across the genome and incorporating LGCs in multi-trait prediction would increase the prediction accuracy by an average of 12.76% ± 2.07% compared to

conventional multi-trait genomic prediction method (MTGBLUP) in the real datasets. Our findings highlight the importance of considering LGCs in improving multi-trait genomic prediction.

SIMILAR CONTENT BEING VIEWED BY OTHERS EFFICIENT WEIGHTING METHODS FOR GENOMIC BEST LINEAR-UNBIASED PREDICTION (BLUP) ADAPTED TO THE GENETIC ARCHITECTURES OF QUANTITATIVE TRAITS Article 26

September 2020 GENOME-WIDE FINE-MAPPING IDENTIFIES PLEIOTROPIC AND FUNCTIONAL VARIANTS THAT PREDICT MANY TRAITS ACROSS GLOBAL CATTLE POPULATIONS Article Open access 08 February 2021

MULTIBREED GENOMIC PREDICTION USING SUMMARY STATISTICS AND A BREED-ORIGIN-OF-ALLELES APPROACH Article Open access 25 May 2023 INTRODUCTION Genomic prediction is a powerful tool for

predicting an individual’s phenotypes or genetic merits of complex traits based on genomic information. It has gained widespread applications in various species, including human, animal, and

plant. In human, genomic prediction has been proven to be valuable in predicting an individual’s risk of developing certain diseases1. This information can be used for personalized

medicine, enabling early intervention and prevention strategies2. In the field of animal and plant breeding, the application of genomic prediction has tremendously accelerated the genetic

gain and reduced breeding costs because of its higher prediction accuracy for genetic merits (breeding values)3. Many complex traits are genetically correlated due to pleotropic effects of

genes on multiple traits4. Since complex traits are influenced by many genes distributed across different genomic regions, genetic correlations between traits should also be results of the

integration of regional or local genetic correlations (LGC), i.e., correlations generated by genes in some genomic regions5. However, genes in different regions may contribute differently to

the global (i.e., genome-wide) genetic correlation, i.e., some regions may produce no correlation, some may produce positive correlations, while some may produce negative correlations6.

Thus, it is very likely that, for a weak (or non-significant) global genetic correlation, there may exist strong LGCs, or for a positive (negative) global genetic correlation, there may

exist negative (positive) LGCs. For example, Zhu et al.7 reported that although the global genetic correlation between AD (Alzheimer’s disease) and T2D (type II Diabetes) and between AD and

LDL (low density lipoprotein) were not significant (\({\hat{r}}_{g}\) = 0.106, _P_ > 0.26 and \({\hat{r}}_{g}\) = 0.104, _P_ > 0.17, respectively), there was a genomic region

(Chr19:44,744,108-46,102,697) that showed highly significant LGCs between AD and T2D (_P_ = 6.78 × 10−22) and between AD and LDL (_P_ = 1.74 × 10−253). Traditionally, multi-trait genomic

prediction only considers the global genetic correlation between different traits and has been proven to be able to increase prediction accuracy in comparison to single trait

prediction8,9,10. However, it can be expected that if we can partition the global genetic correlation into LGCs and use these LGCs, instead of global genetic correlation, in the multi-trait

prediction, the prediction accuracy could be improved because LGCs reflect more accurately the nature of genetic correlation. Theoretically, LGCs can be estimated using individual-level

phenotypes on multi-traits and genotypes of regional genetic variants via the genomic residual maximum likelihood (GREML) approach11 (or similar methods based on individual-level data).

However, it will be computationally challenging or even infeasible because of the very large number of genomic regions. In addition, in some case, individual-level data are not available due

to privacy concerns. Recently, several methods have been developed for estimating LGCs using summary statistics from genome-wide association studies (GWAS), such as _ρ_-HESS12,

SUPERGNOVA13, and LAVA14. Zhang et al.15 conducted a benchmark comparison of the performance of these methods and found that LAVA could provide unbiased estimation with well-controlled

type-I error when using an in-sample reference panel. LGCs have been successfully incorporated in human complex trait analysis16,17,18. These studies proved that LGC analysis could be used

to quantify the genetic similarity of complex traits in specific genomic regions and thus reveal the shared biological mechanisms across traits. Whether incorporating LGCs into multi-trait

genomic prediction would improve the prediction accuracy have not been reported yet. In this study, we present three models for incorporating LGCs into multi-trait genomic prediction. We

used simulated data and three real datasets from human, cow, and pig populations to evaluate the performance of these models. Through comprehensive analyses, we demonstrated the superior

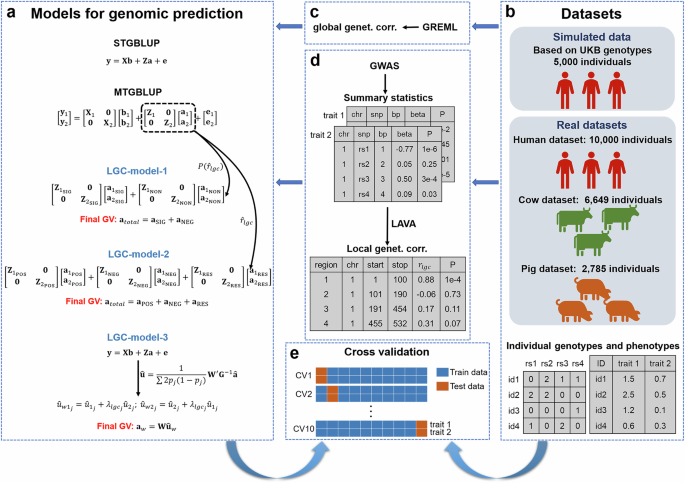
performance of our models compared to the conventional multi-trait genomic prediction model which uses global genetic correlation. RESULTS OVERVIEW OF THE STUDY Figure 1 provides an overview

of our study. Briefly, we introduced three models (LGC-model-1, LGC-model-2, and LGC-model-3) aiming at incorporating LGCs into the multi-trait genomic prediction model (Fig. 1a).

LGC-model-1 considers the significance of LGCs and divides the genomic regions into two groups, i.e., regions with significant LGCs and regions without significant LGCs. LGC-model-2

considers the size and direction of LGCs, and divides the genomic regions into three groups, i.e., regions with strong positive LGCs, regions with strong negative LGCs, and the rest regions.

LGC-model-3 accounts for LGCs by simply adjusting the SNP effects for a trait estimated from single trait model using LGC weighted SNP effects for the other trait. We used simulated data

and real datasets from human, cow, and pig populations (Fig. 1b) to evaluate the performances of these models. We estimated global genetic correlations between traits in the real datasets

using GREML (Fig. 1c) and LGCs using LAVA and GWAS summary statistics (Fig. 1d). Finally, we performed 10-fold cross validations to evaluate the prediction accuracies of these LGC models in

comparison with other genomic prediction models (Fig. 1e). Detailed descriptions of the method and the datasets can be found in the Methods section. SIMULATION STUDY The simulation was based

on the real genotype data from the UK Biobank19. We considered three scenarios with respect to different settings on LGCs, global genetic correlations, and heritabilities (Supplementary

Table 1). Figure 2 shows the prediction accuracies from PRSice-2(C + T), LDpred2, STGBLUP (single trait GBLUP), wMT-BLUP, MTGBLUP and the three LGC models with thresholds _P_ = 0.05 for

LGC-model-1 and LGC-model-3 and \(|{r}_{{lgc}}|\) = 0.5 for LGC-model-2. As expected, in all cases, multi-trait models (MTGBLUP and the LGC models) outperformed the single-trait models

(PRSice-2(C + T), LDpred2 and STGBLUP) and wMT-BLUP, except for trait pairs with zero or very weak global genetic correlations, for which MTGBLUP performed similar to STGBLUP (Fig. 2a).

wMT-BLUP performed worst in most cases, only when the global genetic correlation between traits is particularly high (\({r}_{g}\) = 0.8) (Fig. 2a) or the heritabilities of the two traits

were small (Fig. 2b), it performed better than PRSice-2(C + T), LDpred2 and STGBLUP, but still worse than MTGBLUP and the LGC-models. In both Scenario 1 (Fig. 2a) and Scenario 2 (Fig. 2b),

where all genomic regions exhibited LGCs ranging from −1 to +1 randomly, with varying global genetic correlations (Scenario 1) or varying heritabilities (Scenario 2) for the two traits,

LGC-model-2 performed the best in all cases and the relative gain in prediction accuracies over MTGBLUP ranged from 1.88% to 2.71% in Scenario 1 and 0.02% to 2.45% in Scenario 2, followed by

LGC-model-1. LGC-model-3 performed very similar to MTGBLUP. In Scenario 3 (Fig. 2c), where there were a few regions with strong LGCs and some with weak LGCs, all the three LGC models

significantly outperformed MTGBLUP in all cases (_P_ < 0.05, Supplementary Table 2), with LGC-model-1 being the best followed by LGC-model-2. The relative gain in accuracies of

LGC-model-1 over MTGBLUP ranged from 89.73% to 134.20%. Additionally, we also calculated the prediction accuracy R2 across methods in relation to the simulated heritability. Overall, the R2

of all models increased with simulated heritability (Supplementary Fig. 1). We compared the potential influences of different settings on the thresholds for the LGC models, i.e., _P_ = 0.01

or 0.05 for LGC-model-1 and LGC-model-3, \(|{r}_{{lgc}}|\) = 0.5 or 0.6 for LGC-model-2. The results are presented in Supplementary Fig. 2. Basically, different thresholds for LGC-model-2

had negligible influence on its performance. For LGC-model-1 and LGC-model-3, in Scenarios 1 and 2, the threshold of _P_ = 0.05 yielded slightly better results than the threshold of _P_ = 

0.01 for both LGC-model-1 and LGC-model-3 in most cases, while in Scenario 3 using _P_ = 0.01 was slightly better than using _P_ = 0.05, but the differences were all not significant

(Supplementary Table 3). GLOBAL AND LOCAL GENETIC CORRELATION ESTIMATION BETWEEN TRAITS FOR THE REAL DATASETS We estimated global genetic correlations between traits for each dataset based

on a bivariate linear mixed model using GREML. The results are shown in Supplementary Fig. 3. These correlations ranged from strong positive (\({\hat{r}}_{g}=0.6375\) for FP-PP (FP: fat

percentage, PP: protein percentage) and \({\hat{r}}_{g}=0.7212\) for LMD-LMP (LMD: loin muscle depth, LMP: lean meat percentage)), medium positive or negative (\({\hat{r}}_{g}=0.3870\) for

LDL-TG (LDL: low density lipoprotein, TG: triglycerides), \({\hat{r}}_{g}=0.2435\) for BF-LMD (BF: backfat thickness), and \({\hat{r}}_{g}\) = -0.3562 for BF-LMP), nearly zero

(\({\hat{r}}_{g}=-0.0580\) for HDL-LDL (HDL: high density lipoprotein)), and to strong negative (\({\hat{r}}_{g}=-0.6382\) for HDL-TG, \({\hat{r}}_{g}=-0.6119\) for MY-FP (MY: milk yield),

and \({\hat{r}}_{g}=-0.5936\) for MY-PP). Using the partitioning algorithm of LAVA14, we divided the genomes into semi-independent LD blocks (regions). We obtained 2272 regions with average

size of 1.21 Mb for the human genome, 2902 regions with average size of 0.86 Mb for the cow genome, and 2354 regions with average size of 0.94 Mb for the pig genome (Supplementary Fig. 4).

We performed GWAS for the traits of interest in the three datasets and then estimated LGCs for all genomic regions and all trait pairs using LAVA and the GWAS summary statistics. The results

are shown in Fig. 3. For each trait pair in the three datasets, the number of regions with significant LGCs at threshold _P_ < 0.01 or _P_ < 0.05, and number of regions with

\(|{r}_{{lgc}}|\) ≥ 0.5 or \(|{r}_{{lgc}}|\) ≥ 0.6 are presented in Supplementary Table 4. Overall, we observed substantial variations in LGCs across different regions for all trait pairs,

from strong positive correlations, to zero correlations, and to strong negative correlations (Fig. 3). Further analysis revealed that for trait pairs with weak global genetic correlations,

the LGCs tended to be distributed evenly around zero (e.g., HDL and LDL in the human dataset, Fig. 3a and Supplementary Fig. 5a), whereas for trait pairs with strong positive or negative

global genetic correlations, the distribution of LGCs tended to be shifted toward the positive side (e.g., FP and PP in the cow dataset, Fig. 3b and Supplementary Fig. 5b, and LMD and LMP in

the pig dataset, Fig. 3c and Supplementary Fig. 5c) or negative side (e.g., MY-FP and MY-PP in the cow dataset, Fig. 3b and Supplementary Fig. 5b), such that the averages of local

correlations tended to be close to the global correlations. The averages of estimated local genetic correlations across all regions are shown in Supplementary Fig. 4 (in the left upper

triangles). Furthermore, in general, the stronger global genetic correlations were, the more regions there were with significant LGCs. ACCURACIES OF GENOMIC PREDICTION IN THE REAL DATASETS

Figure 4 shows the prediction accuracies of the seven models with different thresholds for the LGC models in the human dataset, i.e., _P_ = 0.01 or 0.05 for LGC-model-1 and LGC-model-3, and

|_r__lgc_| = 0.5 or 0.6 for LGC-model-2. Again, MTGBLUP and LGC models outperformed single trait methods (PRSice-2(C + T) and STGBLUP) and wMT-BLUP in all cases except for trait pair

HDL-LDL, which had nearly zero global genetic correlation (\({\hat{r}}_{g}=-0.0580\)), MTGBLUP performed similarly to PRSice-2(C + T), STGBLUP and wMT-BLUP. In all cases, LGC-model-1 and

LGC-model-2 outperformed MTGBLUP. The relative superiority of LGC-model-1 over MTGBLUP ranged from 9.46% to 135.97%, and the relative superiority of LGC-model-2 over MTGBLUP ranged from

8.93% to 57.30%. LGC-model-3 performed similar to or slightly better than MTGBLUP. As observed in the simulation study, different thresholds for LGC-model-2 (|_r__lgc_| = 0.5 or 0.6) had

little effect on the accuracy, but different thresholds for LGC-model-1 (_P_ = 0.01 or 0.05) had significant effect (Supplementary Table 5). LGC-model-1 with a threshold of _P_ = 0.05 (Fig. 

4a, b) performed in general better than LGC-model-1 with _P_ = 0.01 (Fig. 4c, d). In addition, with _P_ = 0.05, LGC-model-1 performed better for HDL and LDL in trait pairs HDL-TG and LDL-TG,

while LGC-model-2 performed better for TG. With _P_ = 0.01, LGC-model-2 performed better than or similar to LGC-model-1 for both traits in these two trait pairs. Moreover, the relative

superiority of LGC-model-1 was related to the number of regions with significant LGCs, i.e., the more such kind of regions, the larger its superiority. For the trait pair HDL-LDL, there were

only five regions with _P_ < 0.05 (Supplementary Table 4), the superiority of LGC-model-1 was also limited. Note that for the trait pair HDL-LDL, there was no LGC with _P_ < 0.01. The

results for the cow dataset are presented in Fig. 5. In summary, PRSice-2(C + T) performed worse than other individual-based prediction methods. wMT-BLUP outperformed PRSice-2(C + T) and

performed worse than STGBLUP, MTGBLUP and LGC models. In addition, the three LGC models outperformed MTGBLUP in all cases. Among the three LGC models, LGC-model-1 performed the best with the

relative superiority over MTGBLUP ranged from 8.20% to 13.58%, followed by LGC-model-2 (ranged from 5.88% to 11.96%). LGC-model-3 was slightly better than MTGBLUP. Within each trait pair,

the traits with higher heritability (_h_2(PP) > _h_2(FP) > _h_2(MY)) received higher accuracies. The results for the pig dataset are presented in Fig. 6. Again, RSice-2(C + T)

performed the worst and the three LGC models performed better than MTGBLUP in all cases, but their superiorities were small. LGC-model-2 was slightly better than the other two LGC models and

its superiority over MTGBLUP ranged from 1.84% to 5.05%. DISCUSSION Multi-trait genomic prediction incorporating genetic correlations between traits can improve the prediction

accuracy8,20,21. However, conventional multi-trait genomic prediction methods (e.g., MTGBLUP) do not capture the potential local shared genetic effects, where the correlation or covariance

between two traits are confined to specific genomic regions. Under the assumption that shared genetic effects are not evenly distributed and are heterogenous in different genomic regions,

LGC analysis can inform the interpretation of global genetic correlations12,13,14. In this study, to investigate the potential effect of LGCs on the accuracy of multi-trait genomic

prediction, we proposed three LGC models which incorporated LGCs as annotations for genomic regions into the multi-trait genomic prediction model. We used simulated data and three real

datasets to examine the performances of the three models. To implement these models, estimates of LGCs are required. As mentioned before, LGCs can be estimated via GREML using

individual-level phenotypes and regional genomic variant genotypes based on the same model as used for global genetic correlation estimation with G being constructed using regional SNP

genotypes. The methods using GWAS summary statistics (e.g., LAVA) can be regarded as approximations of GREML22,23. To get the detailed insights about the differences between the two kinds of

approaches, we selected two pairs of traits, FP and PP in the cow dataset and BF and LMD in the pig dataset, and estimated their LGCs via GREML. It turned out that the correlations between

the LAVA and GREML estimates were quite high, ~0.74 for both trait pairs (Supplementary Fig. 6a, b). For FP and PP, the LAVA estimates tended to be larger than the GREML estimates,

especially when the local genetic correlation was negative. In view of the computing time (Supplementary Fig. 6c), LAVA and GREML consumed 0.36 and 84.96 minutes per region on average for

the FP and PP pair (6649 individuals), respectively, and 0.18 and 6.86 minutes for the BF and LMD pair (2794 individuals), respectively. Therefore, for large dataset, GREML is very

computationally challenging and even infeasible, but LAVA is very computationally efficient while maintaining acceptable accuracy. In addition, we compared the prediction accuracy of

LGC-model-2 for these two trait pairs using the GREML or LAVA estimates of LGC (Supplementary Fig. 6d, e). LGC-model-2-GREML performed similar to or slightly better than LGC-model-2-LAVA.

Based on these results, we used LAVA to estimate LGCs for all trait pairs in this study. The LGC analysis for the three real datasets revealed that the LGCs were very heterogenous across the

genome. Although the direction of most LGCs for a trait pair was generally consistent with the direction of the global genetic correlation, particularly for trait pairs showing a strong

global genetic correlation, there was LGCs with opposite direction in some regions. For instance, for the trait pair FP-PP in the cow dataset, which has a strong positive global genetic

correlation (\({\hat{r}}_{g}=0.6375\)), we observed a few regions with strong negative LGCs (\({\hat{r}}_{{lgc}}\le -0.5\) or −0.6, Fig. 3b, Supplementary Table 4). Notably, the region

Chr14:0-0.9 Mb exhibiting the most significant correlation (\({\hat{r}}_{{lgc}}=0.8788\), _P_ = 1.11 × 10−17) coincides with the well-known fact that this region harbors the _DGAT1_ gene

which has pleiotropic effects on both FP and PP24,25. On the other hand, significant LGCs were detected for trait pairs with weak global genetic correlation. For example, for the trait pair

HDL-LDL in the human dataset, which has a nearly zero global genetic correlation (\({\hat{r}}_{g}=-0.0580\)), which is consistent with the findings from previous studies12,14, we detected

five regions with significant LGCs (_P_ < 0.05), four positive and one negative. In this study, we proposed three LGC models for multi-trait genomic prediction. LGC-model-1 takes LGCs

into account by partitioning the genome into regions with significant LGCs (with certain threshold) and regions without significant LGCs. LGC-model-2 considers the size and direction of LGCs

and partitions the genome into regions with strong positive LGCs (with certain threshold), regions with strong negative LGCs, and the rest regions (with weak or zero LGCs). LGC-model-3

accounts for LGCs by simply adjusting the SNP effects for a trait estimated from single trait model (STGBLUP) using LGC-weighted SNP effects for the other trait. We evaluated the

performances of the three LGC models using simulated data and three real datasets. Since LGC-model-3 performed worse than LGC-model-1 and LGC-model-2 in both simulation and the real data in

all cases, we focus on LGC-model-1 and LGC-model-2. The relative improvements in prediction accuracy of LGC-model-1 and LGC-model-2 over MTGBLUP ranged from 0.04% to 134.20% and 0.02% to

81.44%, respectively, for the simulated data and from 1.46% to 135.97% and 1.84% to 57.00%, respectively, for the real data. In general, they have larger superiority for trait pairs with

higher global genetic correlation. For the simulated data, LGC-model-2 performed better in Scenarios 1 and 2, where it was assumed that LGC occurred in all regions taking a value of −1 to +1

randomly. However, LGC-model-1 performed better in Scenario 3, where there were a few regions with strong LGCs. For the human dataset, the superiority of the two models varied with

different traits and different thresholds for LGC-model-1. For the cow dataset, LGC-model-1 performed consistently better for all trait pairs and all threshold values, while for the pig

dataset, LGC-model-2 performed slightly better in most cases. The relative superiority of LGC-model-1 over LGC-model-1 was related to the number of regions with significant LGCs

(Supplementary Table 4), i.e., the more such kind of regions, the larger its superiority. It should be noted that even for trait pairs without global genetic correlation (e.g., the trait

pair with _r__g_ = 0 in Scenario 1 of the simulated data (Fig. 2a) and the trait pair HDL-LDL in the human dataset (Fig. 4)), for which the MTGBLUP model hardly improved the prediction

accuracy over the STGBLUP model, while both of the two LGC models could improve remarkably the prediction accuracy because of the presence of LGCs. Since the relative superiority of

LGC-model-1 and LGC-model-2 differ in different scenarios, it is important to select the optimal model for a given real dataset. From the results in the simulated data and real datasets, we

found that, for a given trait pair, the relative superiority of the two models was almost exclusively depending on the nature of LGCs between the two traits, while irrelevant to the

heritabilities of both traits and the global genetic correlation between them. Therefore, the model selection could be based on the results of the estimated genome-wide LGCs and their

corresponding _P_ values for the trait pair. We suggest the following general strategy for model selection: 1) if there are considerable regions with significant LGCs for the given threshold

(in this case, the trait pair usually has strong global genetic correlation), such as in the case of the cow dataset, LGC-model-1 is preferred; 2) otherwise, either LGC-model-1 or

LGC-model-2 can be used, as their performances did not differ significantly. However, we recommend using LGC-model-2 because it performed slightly better in most cases. Once the optimal

model is selected, another issue to be considered is to determine the threshold for the corresponding model. In this study, we set the threshold _P_ = 0.01 or 0.05 for LGC-model-1, and the

threshold LGC value |_r__lgc_| = 0.5 or 0.6 for LGC-model-2. We found that for LGC-model-2 different thresholds did not significantly change its performance in both simulated and real

datasets (Supplementary Tables 3 and 5) and the threshold |_r__lgc_| = 0.5 were slightly better (but not significant) in most cases. For LGC-model-1, the threshold of _P_ = 0.01 performed

better than or similar to the threshold of _P_ = 0.05 in most cases. There were some cases where _P_ = 0.05 was better, such as for trait pairs HDL-TG and LDL-TG in the human dataset and for

some trait pairs in Scenarios 1 and 2 in the simulation. However, it should be noted that, for all these trait pairs, there were very few regions with _P_ < 0.01 (Supplementary Table 4),

such that using the threshold of _P_ = 0.01 could not efficiently capture the local genetic correlations and even not feasible when there were no such regions, e.g., for the trait pair

HDL-LDL in the human dataset. In view of this problem and the relative performances of the two thresholds, we suggest to use _P_ = 0.01 as priority and use _P_ = 0.05 in cases there are too

few regions with _P_ < 0.01. It should be noted that the polygenicity of the traits may have an impaction on the relative performance of difference models. In the simulation, we found

that for traits with high polygenicity and without major-effect regions, such as those in Scenario 1 and 2, LGC-model-2 performed the best. Conversely, for traits which are less polygenic

but with a few major-effect regions, as observed in Scenario 3, LGC-model-1 performed the best. However, for real datasets, it is hardly to get the information of polygenicity of the traits.

In conclusion, we demonstrate that LGCs among traits are pervasive and heterogeneous. Incorporating LGCs into multi-trait genomic prediction could improve universally the prediction

accuracy and the relative improvement over the conventional MTGBLUP reached up to 135.97% (~12.76% on average) in the real datasets used in this study. Our findings hold promise for

wide-ranging applications of LGCs in multi-trait genomic prediction across diverse traits and species. METHODS GLOBAL GENETIC CORRELATION ESTIMATION VIA GREML A bivariate linear mixed model

(LMM) was used to estimate the global genetic correlation between two traits. The bivariate model is as follows, $$\left[\begin{array}{c}{{{{\bf{y}}}}}_{1}\\

{{{{\bf{y}}}}}_{2}\end{array}\right] = \left[\begin{array}{cc}{{{{\bf{X}}}}}_{1} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{X}}}}}_{2}\end{array}\right]\left[\begin{array}{c}{{{{\bf{b}}}}}_{1}\\ {{{{\bf{b}}}}}_{2}\end{array}\right] +\left[\begin{array}{cc}{{{{\bf{Z}}}}}_{1} & {{{\bf{0}}}}\\

{{{\bf{0}}}} & {{{{\bf{Z}}}}}_{2}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{1}\\ {{{{\bf{a}}}}}_{2}\end{array}\right] + \left[\begin{array}{c}{{{{\bf{e}}}}}_{1}\\

{{{{\bf{e}}}}}_{2}\end{array}\right]\, \\ \left[\begin{array}{c}{{{{\bf{a}}}}}_{1}\\ {{{{\bf{a}}}}}_{2}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{\bf{M}}}}{\scriptstyle{\otimes }}{{{\bf{G}}}}\right),\,\left[\begin{array}{c}{{{{\bf{e}}}}}_{1}\\ {{{{\bf{e}}}}}_{2}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{\bf{R}}}}{\scriptstyle{\otimes }} {{{\bf{I}}}}\right)$$ (1) where \({{{{\bf{y}}}}}_{1}\) and \({{{{\bf{y}}}}}_{2}\) are the vectors of phenotypes

for trait 1 and trait 2, respectively; \({{{{\bf{b}}}}}_{1}\) and \({{{{\bf{b}}}}}_{2}\) are the vectors of fixed effect for the two traits, \({{{{\bf{X}}}}}_{1}\) and \({{{{\bf{X}}}}}_{2}\)

are the their corresponding design matrices, which relate the effects in \({{{{\bf{b}}}}}_{1}\) and \({{{{\bf{b}}}}}_{2}\) to the phenotypes in \({{{{\bf{y}}}}}_{1}\) and

\({{{{\bf{y}}}}}_{2}\); \({{{{\bf{a}}}}}_{1}\) and \({{{{\bf{a}}}}}_{2}\) are the vectors of the genomic merits (additive genetic effects) for the two traits, \({{{{\bf{Z}}}}}_{1}\) and

\({{{{\bf{Z}}}}}_{2}\) are their corresponding design matrices, which relate the effects in \({{{{\bf{a}}}}}_{1}\) and \({{{{\bf{a}}}}}_{2}\) to the phenotypes in \({{{{\bf{y}}}}}_{1}\) and

\({{{{\bf{y}}}}}_{2}\), \({{{\bf{M}}}}=\left[\begin{array}{cc}{\sigma }_{{{{{\rm{a}}}}}_{1}}^{2} & {\sigma }_{{{{{\rm{a}}}}}_{12}}\\ {\sigma }_{{{{{\rm{a}}}}}_{21}} & {\sigma

}_{{{{{\rm{a}}}}}_{2}}^{2}\end{array}\right]\) with \({\sigma }_{{{{{\rm{a}}}}}_{1}}^{2}\) and \({\sigma }_{{{{{\rm{a}}}}}_{2}}^{2}\) being the additive genetic variances and \({\sigma

}_{{{{{\rm{a}}}}}_{12}}\) and \({\sigma }_{{{{{\rm{a}}}}}_{21}}\) being the additive genetic covariance for the two traits, \({{{\bf{G}}}}=\frac{{{{\bf{WW}}}}^{\prime} }{\sum

2{p}_{j}\left(1-{p}_{j}\right)}\) is the genomic relationship matrix (GRM), which was constructed using the method of VanRaden, \({{{\bf{W}}}}\) being the centralized SNP genotype matrix

with element _w__ij_ = _m__ij_–2_p__j_, _m__ij_ being the genotype code (0, 1, and 2 for genotypes 11, 12, and 22, respectively) for individual _i_ and SNP _j_, \({p}_{j}\) being the minor

allele frequency of SNP _j_; \({{{{\bf{e}}}}}_{1}\) and \({{{{\bf{e}}}}}_{2}\) are the vector of the random residuals of the two traits, \({{{\bf{R}}}}=\left[\begin{array}{cc}{\sigma

}_{{{{{\rm{e}}}}}_{1}}^{2} & {\sigma }_{{{{{\rm{e}}}}}_{12}}\\ {\sigma }_{{{{{\rm{e}}}}}_{21}} & {\sigma }_{{{{{\rm{e}}}}}_{2}}^{2}\end{array}\right]\) with \({\sigma

}_{{{{{\rm{e}}}}}_{1}}^{2}\) and \({\sigma }_{{{{{\rm{e}}}}}_{2}}^{2}\) being the residual variances and \({\sigma }_{{{{{\rm{e}}}}}_{12}}\) and \({\sigma }_{{{{{\rm{e}}}}}_{21}}\) being the

residual covariance for the two traits. We used GREML and the software GCTA26 to estimate the variance and covariance components involved in the model. The global genetic correlation was

calculated as \({r}_{g}=\frac{{\sigma }_{{{{{\rm{a}}}}}_{12}}}{\sqrt{{\sigma }_{{{{{\rm{a}}}}}_{1}}^{2}{\sigma }_{{{{{\rm{a}}}}}_{2}}^{2}}}\). The likelihood-ratio test (LRT) between a model

constraining \({r}_{g}\) to be 0 and the unconstrained model was used to test the significance of global genetic correlation. LOCAL GENETIC CORRELATION ESTIMATION The LAVA software14 was

used to estimate the pairwise local genetic correlations between traits based on GWAS summary statistics. We first used the partitioning algorithm implemented in LAVA to divide the genome

into semi-independent blocks as described by Werme et al.14 using genotype data of all individuals in each dataset. This algorithm divides the genome by recursively splitting the largest

block into two smaller blocks, selecting a new breakpoint that minimizes local LD between the resulting blocks. Then, we performed single-trait GWAS based on imputed sequence data and linear

mixed model using GCTA26 for each trait to obtain the summary statistics data required for LAVA. Finally, the run.univ.bivar function of LAVA was run to estimate local genetic correlations.

GENOMIC PREDICTION MODELS STGBLUP The STGBLUP (single-trait genomic BLUP) model was used for genomic prediction for each trait separately. Here, the genetic correlations between traits were

completely ignored. The model is as follows, $${{{\bf{y}}}} \, = \, {{{\bf{X}}}}{{{\bf{b}}}}+{{{\bf{Za}}}}+{{{\bf{e}}}} \\ {{{\bf{a}}}} \, \sim \, N\left(0,{{{\bf{G}}}}{\sigma

}_{{{{\rm{a}}}}}^{2}\right),\,{{{\bf{e}}}} \sim N\left(0,{{{\bf{I}}}}{\sigma }_{{{{\rm{e}}}}}^{2}\right)$$ (2) where \({{{\bf{y}}}}\) is the vector of phenotypic values of the trait,

\({{{\bf{b}}}}\) is the vector of fixed effects, \({{{\bf{X}}}}\) is the design matrix for B, A is the vector of genomic merits, Z is the design matrix for A, \({\sigma

}_{{{{\rm{a}}}}}^{2}\) is the addictive genetic variance and G is the GRM as defined in Model (1), E is the vector of the random residuals, and \({\sigma }_{{{{\rm{e}}}}}^{2}\) is the

residual variance. MTGBLUP MTGBLUP (multi-trait genomic BLUP) is a conventional model for multi-trait genomic prediction, which employs global genetic correlation between traits, while

ignoring local genetic correlations. The MTGBLUP model is as follows, $$\left[\begin{array}{c}{{{{\bf{y}}}}}_{1}\\ {{{{\bf{y}}}}}_{2}\end{array}\right] =

\left[\begin{array}{cc}{{{{\bf{X}}}}}_{1} & {{{\bf{0}}}}\\ {{{\bf{0}}}} & {{{{\bf{X}}}}}_{2}\end{array}\right]\left[\begin{array}{c}{{{{\bf{b}}}}}_{1}\\

{{{{\bf{b}}}}}_{2}\end{array}\right]+\left[\begin{array}{cc}{{{{\bf{Z}}}}}_{1} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{Z}}}}}_{2}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{1}\\ {{{{\bf{a}}}}}_{2}\end{array}\right]+\left[\begin{array}{c}{{{{\bf{e}}}}}_{1}\\

{{{{\bf{e}}}}}_{2}\end{array}\right] \\ \left[\begin{array}{c}{{{{\bf{a}}}}}_{1}\\ {{{{\bf{a}}}}}_{2}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{\bf{M}}}}{\scriptstyle{\bigotimes }} {{{\bf{G}}}}\right),\,\left[\begin{array}{c}{{{{\bf{e}}}}}_{1}\\ {{{{\bf{e}}}}}_{2}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{\bf{R}}}}{\scriptstyle{\bigotimes }} {{{\bf{I}}}}\right)\,$$ (3) The terms (\({{{{\bf{y}}}}}_{1}\), \({{{{\bf{y}}}}}_{2}\), \({{{{\bf{b}}}}}_{1}\),

and \({{{{\bf{b}}}}}_{2}\), respectively) are the same as those in Model (1). As previously described above, the MTGBLUP assumes that all available SNPs contribute equally to the two traits

and have the same covariance, which limits its prediction accuracy. LGC-MODEL-1 The LMM model can model multiple random effects and hence estimate multiple genetic variances using multiple

GRMs, each built with SNPs selected on different regions. In this model, the genome is divided into two parts, the first part contains all regions with significant local genetic correlations

(SIG) and the second part contains all regions with non-significant local genetic correlations (NON). The threshold of _P_ value for the significance was set as 0.01 or 0.05. The model is

as follows, $$\left[\begin{array}{c}{{{{\bf{y}}}}}_{1}\\ {{{{\bf{y}}}}}_{2}\end{array}\right] = \left[\begin{array}{cc}{{{{\bf{X}}}}}_{1} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{X}}}}}_{2}\end{array}\right]\left[\begin{array}{c}{{{{\bf{b}}}}}_{1}\\ {{{{\bf{b}}}}}_{2}\end{array}\right] \\ + \left[\begin{array}{cc}{{{{\bf{Z}}}}}_{{1}_{{{{\rm{SIG}}}}}} &

{{{\bf{0}}}}\\ {{{\bf{0}}}} & {{{{\bf{Z}}}}}_{{2}_{{{{\rm{SIG}}}}}}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{SIG}}}}}}\\

{{{{\bf{a}}}}}_{{2}_{{{{\rm{SIG}}}}}}\end{array}\right]+\left[\begin{array}{cc}{{{{\bf{Z}}}}}_{{1}_{{{{\rm{NON}}}}}} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{Z}}}}}_{{2}_{{{{\rm{NON}}}}}}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{NON}}}}}}\\ {{{{\bf{a}}}}}_{{2}_{{{{\rm{NON}}}}}}\end{array}\right] \\

+\left[\begin{array}{c}{{{{\bf{e}}}}}_{1} \\ {{{{\bf{e}}}}}_{2}\end{array}\right] \left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{SIG}}}}}}\\

{{{{\bf{a}}}}}_{{2}_{{{{\rm{SIG}}}}}}\end{array}\right] \sim {{{\boldsymbol{N}}}}\left({{{\boldsymbol{0}}}},{{{{\bf{M}}}}}_{{{{\rm{SIG}}}}}{\scriptstyle{\bigotimes }}

{{{{\bf{G}}}}}_{{{{\rm{SIG}}}}}\right),\,\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{NON}}}}}}\\ {{{{\bf{a}}}}}_{{2}_{{{{\rm{NON}}}}}}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\boldsymbol{0}}}},{{{{\bf{M}}}}}_{{{{\rm{NON}}}}}{\scriptstyle{\bigotimes }} {{{{\bf{G}}}}}_{{{{\rm{NON}}}}}\right)$$ (4) where

\({{{{\bf{a}}}}}_{{1}_{{{{\rm{SIG}}}}}}\) and \({{{{\bf{a}}}}}_{{2}_{{{{\rm{SIG}}}}}}\) are the vectors of genomic merits owing to the SIG regions for the two traits,

\({{{{\bf{G}}}}}_{{{{\rm{SIG}}}}}\) is the GRM constructed using SNPs in the SIG regions, \({{{{\bf{M}}}}}_{{{{\rm{sig}}}}}=\left[\begin{array}{cc}{\sigma

}_{{{{{\rm{a}}}}}_{{1}_{{{{\rm{SIG}}}}}}}^{2} & {\sigma }_{{{{{\rm{a}}}}}_{{12}_{{{{\rm{SIG}}}}}}}\\ {\sigma }_{{{{{\rm{a}}}}}_{{21}_{{{{\rm{SIG}}}}}}} & {\sigma

}_{{{{{\rm{a}}}}}_{{2}_{{{{\rm{SIG}}}}}}}^{2}\end{array}\right]\) is the additive genetic variance-covariance matrix of the two traits for the SIG regions;

\({{{{\bf{a}}}}}_{{1}_{{{{\rm{NON}}}}}}\), \({{{{\bf{a}}}}}_{{2}_{{{{\rm{NON}}}}}}\), \({{{{\bf{G}}}}}_{{{{\rm{NON}}}}}\) and \({{{{\bf{M}}}}}_{{{{\rm{NON}}}}}\) are the counterparts of the

above terms for the NON regions. The rest terms (\({{{{\bf{y}}}}}_{1}\), \({{{{\bf{y}}}}}_{2}\), \({{{{\bf{b}}}}}_{1}\), and \({{{{\bf{b}}}}}_{2}\)) are the same as those in Model (1). In

this model, the total genetic values for the two traits are defined as: $${{{{\bf{a}}}}}_{{1}_{{total}}}={{{{\bf{a}}}}}_{{1}_{{{{\rm{SIG}}}}}}+{{{{\bf{a}}}}}_{{1}_{{{{\rm{NON}}}}}}$$

$${{{{\bf{a}}}}}_{{2}_{{total}}}={{{{\bf{a}}}}}_{{2}_{{{{\rm{SIG}}}}}}+{{{{\bf{a}}}}}_{{2}_{{{{\rm{NON}}}}}}$$ LGC-MODEL-2 In this model, the genome is divided into three parts. The first

part contains all regions with strong positive local genetic correlations (POS), the second part contains all regions with strong negative local genetic correlations (NEG), and the third

part contains all rest regions (RES). The threshold for the strong positive (negative) correlation is set as |_r__lgc_| = 0.5 or 0.6 (_r__lgc_ stands for local genetic correlation). The

model is as follows, $$\left[\begin{array}{c}{{{{\bf{y}}}}}_{1}\\ {{{{\bf{y}}}}}_{2}\end{array}\right] = \left[\begin{array}{cc}{{{{\bf{X}}}}}_{1} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{X}}}}}_{2}\end{array}\right]\left[\begin{array}{c}{{{{\bf{b}}}}}_{1}\\ {{{{\bf{b}}}}}_{2}\end{array}\right]+ \left[\begin{array}{cc}{{{{\bf{Z}}}}}_{{1}_{{{{\rm{POS}}}}}} &

{{{\bf{0}}}}\\ {{{\bf{0}}}} & {{{{\bf{Z}}}}}_{{2}_{{{{\rm{POS}}}}}}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{POS}}}}}}\\

{{{{\bf{a}}}}}_{{2}_{{{{\rm{POS}}}}}}\end{array}\right]+\left[\begin{array}{cc}{{{{\bf{Z}}}}}_{{1}_{{{{\rm{NEG}}}}}} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{Z}}}}}_{{2}_{{{{\rm{NEG}}}}}}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{NEG}}}}}}\\ {{{{\bf{a}}}}}_{{2}_{{{{\rm{NEG}}}}}}\end{array}\right] \\

+\left[\begin{array}{cc}{{{{\bf{Z}}}}}_{{1}_{{{{\rm{RES}}}}}} & {{{\bf{0}}}}\\ {{{\bf{0}}}} &

{{{{\bf{Z}}}}}_{{2}_{{{{\rm{RES}}}}}}\end{array}\right]\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{RES}}}}}}\\

{{{{\bf{a}}}}}_{{2}_{{{{\rm{RES}}}}}}\end{array}\right]+\left[\begin{array}{c}{{{{\bf{e}}}}}_{1}\\ {{{{\bf{e}}}}}_{2}\end{array}\right] \\

\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{POS}}}}}} \\ {{{{\bf{a}}}}}_{{2}_{{{{\rm{POS}}}}}}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{{\bf{M}}}}}_{{{{\rm{POS}}}}}{\scriptstyle{\bigotimes }}

{{{{\bf{G}}}}}_{{{{\rm{POS}}}}}\right);{{{{\bf{M}}}}}_{{{{\rm{POS}}}}}=\left[\begin{array}{cc}{\sigma }_{{{{{\rm{a}}}}}_{{1}_{{{{\rm{POS}}}}}}}^{2} & {\sigma

}_{{{{{\rm{a}}}}}_{{12}_{{{{\rm{POS}}}}}}}\\ {\sigma }_{{{{{\rm{a}}}}}_{{21}_{{{{\rm{POS}}}}}}} & {\sigma }_{{{{{\rm{a}}}}}_{{2}_{{{{\rm{POS}}}}}}}^{2}\end{array}\right] \\

\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{NEG}}}}}}\\ {{{{\bf{a}}}}}_{{2}_{{{{\rm{NEG}}}}}}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{{\bf{M}}}}}_{{{{\rm{NEG}}}}}{\scriptstyle{\bigotimes

}}{{{{\bf{G}}}}}_{{{{\rm{NEG}}}}}\right);{{{{\bf{M}}}}}_{{{{\rm{NEG}}}}}=\left[\begin{array}{cc}{\sigma }_{{{{{\rm{a}}}}}_{{1}_{{{{\rm{NEG}}}}}}}^{2} & {\sigma

}_{{{{{\rm{a}}}}}_{{12}_{{{{\rm{NEG}}}}}}}\\ {\sigma }_{{{{{\rm{a}}}}}_{{21}_{{{{\rm{NEG}}}}}}} & {\sigma }_{{{{{\rm{a}}}}}_{{2}_{{{{\rm{NEG}}}}}}}^{2}\end{array}\right] \\

\left[\begin{array}{c}{{{{\bf{a}}}}}_{{1}_{{{{\rm{RES}}}}}}\\ {{{{\bf{a}}}}}_{{2}_{{{{\rm{RES}}}}}}\end{array}\right] \sim

{{{\boldsymbol{N}}}}\left({{{\bf{0}}}},{{{{\bf{M}}}}}_{{{{\rm{RES}}}}}{\scriptstyle{\bigotimes

}}{{{{\bf{G}}}}}_{{{{\rm{RES}}}}}\right);{{{{\bf{M}}}}}_{{{{\rm{RES}}}}}=\left[\begin{array}{cc}{\sigma }_{{{{{\rm{a}}}}}_{{1}_{{{{\rm{RES}}}}}}}^{2} & {\sigma

}_{{{{{\rm{a}}}}}_{{12}_{{{{\rm{RES}}}}}}}\\ {\sigma }_{{{{{\rm{a}}}}}_{{21}_{{{{\rm{RES}}}}}}} & {\sigma }_{{{{{\rm{a}}}}}_{{2}_{{{{\rm{RES}}}}}}}^{2}\end{array}\right]$$ (5) All the

terms in the model are the same as those in Model (1) with the subscripts POS, NEG, and RES refer to the corresponding genomic regions. In this model, the total genetic values for two traits

are defined as: $${{{{\bf{a}}}}}_{{1}_{{total}}}={{{{\bf{a}}}}}_{{1}_{{{{\rm{POS}}}}}}+{{{{\bf{a}}}}}_{{1}_{{{{\rm{NEG}}}}}}+{{{{\bf{a}}}}}_{{1}_{{{{\rm{RES}}}}}}$$

$${{{{\bf{a}}}}}_{{2}_{{total}}}={{{{\bf{a}}}}}_{{2}_{{{{\rm{POS}}}}}}+{{{{\bf{a}}}}}_{{2}_{{{{\rm{NEG}}}}}}+{{{{\bf{a}}}}}_{{2}_{{{{\rm{RES}}}}}}$$ LGC-MODEL-3 In this model, we first

estimate the SNP effects from the estimated genomic merits for each trait derived from the STGBLUP model, using the method proposed by previous studies27,28,

$$\hat{{{{\bf{u}}}}}=\frac{1}{\sum 2{p}_{j}\left(1-{p}_{j}\right)}{{{{\bf{W}}}}}^{{\prime} }{{{{\bf{G}}}}}^{-1}\hat{{{{\bf{a}}}}}$$ where \(\hat{{{{\bf{u}}}}}\) is the vector of estimated

SNP effects; \(\hat{{{{\bf{a}}}}}\) is the vector of estimated genomic merits, \({p}_{j}\), \({{{\bf{W}}}}\), and \({{{\bf{G}}}}\) are the same as those in Model (1). Some studies

constructed multi-trait genetic predictors by combining single-trait predictors to improve prediction accuracy8,29. If two traits are genetically correlated, there will be correlations

between SNP effects for the two traits30. Thus, the effect of a SNP for a trait can be partitioned into two parts, one is its direct effect on the trait, the second is its indirect effect

through the other trait. Inspired by the above two points, using the estimated SNP effects for the two traits and the estimated local genetic correlations, we adjust SNP effects as follows,

$${\hat{u}}_{{{{{\rm{w}}}}1}_{j}}={\hat{u}}_{{1}_{j}}+{\lambda }_{{{lgc}}_{j}}{\hat{u}}_{{2}_{j}};{\hat{u}}_{{{{\rm{w}}}}{2}_{j}}={\hat{u}}_{{2}_{j}}+{\lambda

}_{{{lgc}}_{j}}{\hat{u}}_{{1}_{j}}$$ $${\lambda }_{{{lgc}}_{j}}=\left\{\begin{array}{c}{\hat{r}}_{{{lgc}}_{j}}, \;{if}\,P({\hat{r}}_{{{lgc}}_{j}}) \, < \, P{{\_}}{threshold}\\

0,\quad{otherwise}\hfill\end{array}\right.$$ where \({\hat{u}}_{{1}_{j}}\) and \({\hat{u}}_{{2}_{j}}\) are the estimated effects of SNP _j_ for the two traits, \({\hat{r}}_{{{lgc}}_{j}}\) is

the estimated local genetic correlation for the region where SNP _j_ is located, \(P({\hat{r}}_{{{lgc}}_{j}})\) is the _P_ value for \({\hat{r}}_{{{lgc}}_{j}}\), and _P_threshold_ is the

significance thresholds (0.01 or 0.05). Finally, the adjusted genetic values for two traits can be calculated as,

$${{{{\bf{a}}}}}_{w1}={{{\bf{W}}}}{\hat{{{{\bf{u}}}}}}_{w1};\,{{{{\bf{a}}}}}_{w2}={{{\bf{W}}}}{\hat{{{{\bf{u}}}}}}_{w2}$$ We also compared LGC models with existing prediction methods:

PRSice-2(C + T)31, LDpred232 and wMT-BLUP8. PRSice-2 and LDpred2 are univariate summary statistics-based prediction methods that only focus on one trait. We constructed the LD matrix for

PRSice-2 and LDpred2 using the 1000 individuals randomly sampled from all individuals in each dataset. The wMT-BLUP is a multi-trait BLUP prediction method that calculates a weighted index

to generate predictors. STGBLUP was used to obtain individual BLUP predictors and wMT-BLUP predictors for the target trait were then calculated using the individual BLUP predictors of the

target trait and relevant traits as input. SIMULATED DATA We conducted a simulation study based on the real genotypes from the UK Biobank data19. Specifically, we randomly selected 5000

individuals with white British descent and only used their SNP genotype data of Chromosome 1 (363,052 SNPs). We simulated their phenotypes on two traits with different heritabilities and

global genetic correlations based on a bivariate model. The chromosome was divided into 162 semi-independent LD regions using the partitioning algorithm of LAVA14. We considered three

scenarios. The first scenario assumed the two traits have the same heritability (\({h}_{1}^{2}={h}_{2}^{2}=0.5\)) but varied global genetic correlations. All of the 162 regions exhibited

non-zero LGCs. We randomly selected 10 SNPs in each region as causal SNPs (1620 causal SNPs in total) for both traits and simulated the effect of the _j_th causal SNP in the _i_th region

(\({\beta }_{{ij}}\)) based on the multivariate normal distribution, \({\beta }_{{ij}} \sim {MVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}0.005 &

{{{\mathrm{cov}}}}_{{g}_{{ij}}}\\ {{{\mathrm{cov}}}}_{{g}_{{ij}}} & 0.005\end{array}\right]\right)\). The LGCs of all regions were obtained from the uniform distribution U[−1, 1]. The

residual effect of _k_th individual (\({e}_{k}\)) were drawn from the multivariate normal distribution, \({e}_{k} \sim {MVN}\left(\left[\begin{array}{c}0\\

0\end{array}\right],\left[\begin{array}{cc}{\sigma }_{{e}_{1}}^{2} & {{{\mathrm{cov}}}}_{e}\\ {{{\mathrm{cov}}}}_{e} & {\sigma }_{{e}_{2}}^{2}\end{array}\right]\right)\), where

\({{{{\rm{\sigma }}}}}_{{e}_{1}}^{2}=(0.005* 1620)(1-{h}_{1}^{2})/{h}_{1}^{2}\), \({{{{\rm{\sigma }}}}}_{{e}_{2}}^{2}=(0.005* 1620)(1-{h}_{2}^{2})/{h}_{2}^{2}\), and

\({{{\mathrm{cov}}}}_{e}={r}_{e}{\sigma }_{{e}_{1}}{\sigma }_{{e}_{2}}\), where \({r}_{e}\) is the residual correlation. The second scenario fixed the global genetic correlation to be 0.6,

but varied the heritabilities of the two traits. The LGCs, SNPs and residual effects were generated in the same way as in scenario 1. The third scenario again had fixed global genetic

correlation of 0.6 but varied heritabilities. In this scenario, we randomly divided the 162 regions into three parts, i.e., 5 regions with strong LGCs and 10 causal SNPs with large effects

on both traits in each region, 20 regions with weak LGCs and 10 causal SNPs in each region, and the rest regions without LGCs and no causal SNPs. The causal SNP effects in the 5 strong

regions were simulated by \({\beta }_{{ij}} \sim {MVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}0.1 & {{{\mathrm{cov}}}}_{{g}_{{ij}}}\\

{{{\mathrm{cov}}}}_{{g}_{{ij}}} & 0.1\end{array}\right]\right)\) and the LGCs of these regions were obtained from U[0.5, 0.9]. The causal SNP effects in the 20 week regions were

generated by sampling from \({\beta }_{{ij}} \sim {MVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\,\left[\begin{array}{cc}0.005 & {{{\mathrm{cov}}}}_{{g}_{{ij}}}\\

{{{\mathrm{cov}}}}_{{g}_{{ij}}} & 0.005\end{array}\right]\right)\) and the local genetic correlations were obtained from U[−0.05, 0.05]. In all scenarios, the integrated genetic

correlation over all these regions should be in corresponding to the global genetic correlation. The residual correlations were set to be 0.2 in all scenarios. The parameter settings for the

three scenarios are given in Supplementary Table 1. It should be noted that the global genetic correlation is equal to the mean of the local genetic correlations because we assumed the

variances of all causal SNPs were equal. For every parameter set, 50 replicates were carried out. REAL DATASETS Three real datasets were used to evaluate the performances of the proposed

models. A summary of these datasets is shown in Table 1. HUMAN DATASET The human dataset was from the UK Biobank (http://www.ukbiobank.ac.uk), which contains extensive phenotype information

from approximately ~500,000 individuals aged between 40 and 69 years old19. Considering computing time, we random selected 10,000 individuals of white British descent. These individuals were

genotyped with UK Biobank Axiom Array and UK BiLEVE Axiom Array, as indicated by UKB Data-field 1001, and the genotype data was imputed to sequence data by the UKB analysis team using the

whole-genome sequence data from the Haplotype Reference Consortium33 and the UK10K project34 as the reference panels. We conducted quality control for the imputed genotype data using

plink1.9 and filtered SNPs with a minor allele frequency (MAF) ≤ 0.05, or with a _P_ value ≤ 1e-6 for Hardy-Weinberg equilibrium (HWE) test, or a call rate <90%. After quality control,

there were 7,798,091 SNPs remained for further analysis. We analyzed three traits for these individuals, i.e., high density lipoprotein (HDL), low density lipoprotein (LDL), and

triglycerides (TG). There were no missing phenotypic values for the three traits for all individuals. COW DATASET The cow dataset consisted of 6649 Chinese Holstein cows. All cows had

official estimated breeding values (EBV) of the Chinese Dairy Association for three milk production traits, i.e., milk yield (MY), fat percentage (FP), and protein percentage (PP). We

converted the EBVs to de-regressed proofs (DRP) using the method of Garrick et al.35 and used DRPs as pseudo phenotypes for these traits in the subsequent analysis. These cows were genotyped

with different types of SNP chips (Illumina Bovine SNP50v1, Illumina Bovine SNP50v2 and GeneSeek Genomic Profiler Bovine HD). We imputed all chip data to whole-genome sequence data using

Beagle536. The detailed imputation procedure is described in our previous study37. After quality control for the genotype data in the same way as for the human dataset, 11,106,834 SNPs

remained for the subsequent analysis. PIG DATASET The pig dataset consists of 2794 Duroc boars and all of tem had phenotypes on three traits: backfat thickness at 100 kg (BF, mm), loin

muscle depth at 100 kg (LMD, mm), and lean meat percentage at 100 kg (LMP). These animals were genotyped with low-coverage whole-genome sequencing at a mean depth of 0.73× and imputed to

high coverage sequence data. The detailed information about the phenotype and genotype data is described in Yang et al.’s study38. After quality control (in the same way as for the human

dataset), 9,913,155 SNPs remained for the subsequent analysis. EVALUATION OF ACCURACIES OF GENOMIC PREDICTION For each dataset, we performed 10-fold cross-validations to assess the accuracy

of genomic prediction based on the models defined above. For the simulated data, the accuracy was assessed by \({r}_{{TGV},{PGV}}\), i.e., the correlation between the true genetic values

(TGV) and the predicted genetic values (PGV) of the validation individuals. For the human and pig datasets, the accuracy was assessed by \({r}_{{y}_{c},{PGV}}\), i.e., the correlation

between corrected phenotypic values (\({y}_{c}\)) and PGV of the validation individuals. The corrected phenotypic values were calculated as the original phenotypic values corrected for fixed

effects (e.g., sex, age, and year-season). For the cow dataset, the accuracy was assessed by \({r}_{{DRP},{EGV}}\), i.e., correlation between DRP and PGV of the validation individuals. We

repeated the cross-validation 10 times for each scenario. STATISTICS AND REPRODUCIBILITY The statistical analyses were conducted in Python version 3.8.5, or various command line tools as

described in the Methods section. This study utilized three datasets: human (10,000 individuals), cow (6649 individuals) and pig (2794 individuals). For the simulation study, 50 replicates

were conducted for each parameter set. In the real dataset analysis, genomic prediction was evaluated through 10-fold cross-validation with 10 replicates. The more details of statistical

analyses, sample sizes and replicates were described in the Methods section above. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting

Summary linked to this article. DATA AVAILABILITY The individual-level genotypes and phenotypes of the human dataset are available through formal application to the UK Biobank

(http://www.ukbiobank.ac.uk). This research has been conducted using the UK Biobank Resource under Application Number 87771. The individual-level genotypes and phenotypes of the cow dataset

are the property of the dairy farmers of China and, thus, are not publicly available. The individual-level genotypes and phenotypes of the pig dataset are available at

https://doi.org/10.5524/100894. All other relevant data are available in this article and its Supplementary Information files. Supplementary Data 1 provides the source data behind the main

figures in the manuscript, and Supplementary Figs. CODE AVAILABILITY The code for running LGC models can be found at GitHub (https://github.com/Tengjun0520/lgc_genomic_prediction) and Zenodo

(https://doi.org/10.5281/zenodo.14836967)39. REFERENCES * Riveros-Mckay, F. et al. Integrated polygenic tool substantially enhances coronary artery disease prediction. _Circ. Genom. Precis.

Med._ 14, e3304 (2021). Article  Google Scholar  * Abraham, G. & Inouye, M. Genomic risk prediction of complex human disease and its clinical application. _Curr. Opin. Genet. Dev._ 33,

10–16 (2015). Article  CAS  PubMed  Google Scholar  * Hayes, B. J., Bowman, P. J., Chamberlain, A. J. & Goddard, M. E. Invited review: genomic selection in dairy cattle: progress and

challenges. _J. Dairy Sci._ 92, 433–443 (2009). Article  CAS  PubMed  Google Scholar  * Stearns, F. W. One hundred years of pleiotropy: a retrospective. _Genetics_ 186, 767–773 (2010).

Article  CAS  PubMed  PubMed Central  Google Scholar  * Pickrell, J. K. et al. Detection and interpretation of shared genetic influences on 42 human traits. _Nat. Genet._ 48, 709–717 (2016).

Article  CAS  PubMed  PubMed Central  Google Scholar  * van Rheenen, W. et al. Genetic correlations of polygenic disease traits: from theory to practice. _Nat. Rev. Genet._ 20, 567–581

(2019). Article  PubMed  Google Scholar  * Zhu, Z. et al. Shared genetic architecture between metabolic traits and Alzheimer’s disease: a large-scale genome-wide cross-trait analysis. _Hum.

Genet._ 138, 271–285 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Maier, R. M. et al. Improving genetic prediction by leveraging genetic correlations among human diseases

and traits. _Nat. Commun._ 9, 989 (2018). Article  PubMed  PubMed Central  Google Scholar  * Albinana, C. et al. Multi-PGS enhances polygenic prediction by combining 937 polygenic scores.

_Nat. Commun._ 14, 4702 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Clark, K. et al. The prediction of Alzheimer’s disease through multi-trait genetic modeling. _Front.

Aging Neurosci._ 15, 1168638 (2023). Article  PubMed  PubMed Central  Google Scholar  * Li, X. et al. The patterns of genomic variances and covariances across genome for milk production

traits between Chinese and Nordic Holstein populations. _BMC Genet._ 18, 26 (2017). Article  PubMed  PubMed Central  Google Scholar  * Shi, H., Mancuso, N., Spendlove, S. & Pasaniuc, B.

Local genetic correlation gives insights into the shared genetic architecture of complex traits. _Am. J. Hum. Genet._ 101, 737–751 (2017). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Zhang, Y. et al. SUPERGNOVA: local genetic correlation analysis reveals heterogeneous etiologic sharing of complex traits. _Genome Biol._ 22, 262 (2021). Article  PubMed  PubMed

Central  Google Scholar  * Werme, J., van der Sluis, S., Posthuma, D. & de Leeuw, C. A. An integrated framework for local genetic correlation analysis. _Nat. Genet._ 54, 274–282 (2022).

Article  CAS  PubMed  Google Scholar  * Zhang, C., Zhang, Y., Zhang, Y. & Zhao, H. Benchmarking of local genetic correlation estimation methods using summary statistics from genome-wide

association studies. _Brief. Bioinform_. 24, bbad407 (2023). * Gerring, Z. F., Thorp, J. G., Gamazon, E. R. & Derks, E. M. A local genetic correlation analysis provides biological

insights into the shared genetic architecture of psychiatric and substance use phenotypes. _Biol. Psychiatry_ 92, 583–591 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Lona-Durazo, F. et al. Regional genetic correlations highlight relationships between neurodegenerative disease loci and the immune system. _Commun. Biol._ 6, 729 (2023). Article  CAS  PubMed

  PubMed Central  Google Scholar  * Stauffer, E. M. et al. The genetic relationships between brain structure and schizophrenia. _Nat. Commun._ 14, 7820 (2023). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Bycroft, C. et al. The UK Biobank resource with deep phenotyping and genomic data. _Nature_ 562, 203–209 (2018). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Bahda, M. et al. Multivariate extension of penalized regression on summary statistics to construct polygenic risk scores for correlated traits. _HGG Adv._ 4, 100209 (2023). CAS 

PubMed  PubMed Central  Google Scholar  * Krapohl, E. et al. Multi-polygenic score approach to trait prediction. _Mol. Psychiatry_ 23, 1368–1374 (2018). Article  CAS  PubMed  Google Scholar

  * Ni, G., Moser, G., Wray, N. R. & Lee, S. H. Estimation of genetic correlation via linkage disequilibrium score regression and genomic restricted maximum likelihood. _Am. J. Hum.

Genet._ 102, 1185–1194 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wu, Y. et al. Fast estimation of genetic correlation for biobank-scale data. _Am. J. Hum. Genet._ 109,

24–32 (2022). Article  CAS  PubMed  Google Scholar  * Jiang, J. et al. Functional annotation and Bayesian fine-mapping reveals candidate genes for important agronomic traits in Holstein

bulls. _Commun. Biol._ 2, 212 (2019). Article  PubMed  PubMed Central  Google Scholar  * Reynolds, E. et al. Non-additive QTL mapping of lactation traits in 124,000 cattle reveals novel

recessive loci. _Genet. Sel. Evol._ 54, 5 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  * Yang, J., Lee, S. H., Goddard, M. E. & Visscher, P. M. GCTA: a tool for

genome-wide complex trait analysis. _Am. J. Hum. Genet._ 88, 76–82 (2011). Article  CAS  PubMed  PubMed Central  Google Scholar  * Stranden, I. & Garrick, D. J. Technical note:

derivation of equivalent computing algorithms for genomic predictions and reliabilities of animal merit. _J. Dairy Sci._ 92, 2971–2975 (2009). Article  CAS  PubMed  Google Scholar  * Wang,

H. et al. Genome-wide association mapping including phenotypes from relatives without genotypes. _Genet. Res._ 94, 73–83 (2012). Article  CAS  Google Scholar  * Xu, C., Ganesh, S. K. &

Zhou, X. mtPGS: Leverage multiple correlated traits for accurate polygenic score construction. _Am. J. Hum. Genet._ 110, 1673–1689 (2023). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Olasege, B. S. et al. Correlation scan: identifying genomic regions that affect genetic correlations applied to fertility traits. _BMC Genomics_ 23, 684 (2022). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Choi, S. W. & O’Reilly, P. F. PRSice-2: polygenic risk score software for biobank-scale data. _Gigascience_ 8, giz082 (2019). * Prive, F.,

Arbel, J. & Vilhjalmsson, B. J. LDpred2: better, faster, stronger. _Bioinformatics_ 36, 5424–5431 (2021). Article  PubMed  Google Scholar  * McCarthy, S. et al. A reference panel of

64,976 haplotypes for genotype imputation. _Nat. Genet._ 48, 1279–1283 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Walter, K. et al. The UK10K project identifies rare

variants in health and disease. _Nature_ 526, 82–90 (2015). Article  CAS  PubMed  Google Scholar  * Garrick, D. J., Taylor, J. F. & Fernando, R. L. Deregressing estimated breeding values

and weighting information for genomic regression analyses. _Genet. Sel. Evol._ 41, 55 (2009). Article  PubMed  PubMed Central  Google Scholar  * Browning, B. L., Zhou, Y. & Browning, S.

R. A one-penny imputed genome from next-generation reference panels. _Am. J. Hum. Genet._ 103, 338–348 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Teng, J. et al.

Longitudinal genome-wide association studies of milk production traits in Holstein cattle using whole-genome sequence data imputed from medium-density chip data. _J. Dairy Sci._ 106,

2535–2550 (2023). Article  CAS  PubMed  Google Scholar  * Yang, R. et al. Accelerated deciphering of the genetic architecture of agricultural economic traits in pigs using a low-coverage

whole-genome sequencing strategy. _Gigascience_ 10, giab048 (2021). Article  PubMed  PubMed Central  Google Scholar  * Teng, J. et al. The code repo for “Improving multi-trait genomic

prediction by incorporating local genetic correlations”. _Zenodo_, https://doi.org/10.5281/zenodo.14836967 (2025). Download references ACKNOWLEDGEMENTS This work was supported by the

National Key Research and Development Program of China (2022YFF1000900 and 2021YFD1200900), Biological Breeding Major Projects (2023ZD04049 and 2023ZD04046), Yangzhou University

Interdisciplinary Research Foundation for Animal Science Discipline of Targeted Support (yzuxk202016), the Project of Genetic Improvement for Agricultural Species of Shandong Province

(2019LZGC011, 2022LZGCQY007 and 2023LZGC004), Shandong Provincial Natural Science Foundation (ZR2020QC175 and ZR2020QC176) and National Natural Science Foundation of China (32002172 and

32370675). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Shandong Provincial Key Laboratory for Livestock Germplasm Innovation & Utilization, College of Animal Science and Technology,

Shandong Agricultural University, Tai’an, China Jun Teng, Xinyi Zhang, Changheng Zhao, Wenwen Wang, Hui Tang, Chao Ning, Dan Wang & Qin Zhang * Shandong Futeng Food Co. Ltd., Zaozhuang,

China Jun Teng * National Key Laboratory of Wheat Improvement, College of Life Science, Shandong Agricultural University, Tai’an, China Tingting Zhai * College of Veterinary Medicine,

Shandong Agricultural University, Tai’an, China Yingli Shang Authors * Jun Teng View author publications You can also search for this author inPubMed Google Scholar * Tingting Zhai View

author publications You can also search for this author inPubMed Google Scholar * Xinyi Zhang View author publications You can also search for this author inPubMed Google Scholar * Changheng

Zhao View author publications You can also search for this author inPubMed Google Scholar * Wenwen Wang View author publications You can also search for this author inPubMed Google Scholar

* Hui Tang View author publications You can also search for this author inPubMed Google Scholar * Chao Ning View author publications You can also search for this author inPubMed Google

Scholar * Yingli Shang View author publications You can also search for this author inPubMed Google Scholar * Dan Wang View author publications You can also search for this author inPubMed 

Google Scholar * Qin Zhang View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Q.Z. and D.W. designed the study. J.T. performed the

experiments. C.Z., X.Z., H.T., C.N., and Y.S. collected the data. J.T., T.Z., W.W., and D.W. analyzed and interpreted the data. J.T. and Q.Z. drafted the manuscript. All authors reviewed the

final manuscript. CORRESPONDING AUTHORS Correspondence to Dan Wang or Qin Zhang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW

INFORMATION _Communications Biology_ thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Aylin Bircan, Christina Karlsson

Rosenthal. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILE SUPPLEMENTARY DATA 1 REPORTING SUMMARY TRANSPARENT PEER REVIEW FILE RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing,

distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and

indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third

party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the

article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright

holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Teng, J., Zhai, T., Zhang, X.

_et al._ Improving multi-trait genomic prediction by incorporating local genetic correlations. _Commun Biol_ 8, 307 (2025). https://doi.org/10.1038/s42003-025-07721-9 Download citation *

Received: 28 June 2024 * Accepted: 11 February 2025 * Published: 25 February 2025 * DOI: https://doi.org/10.1038/s42003-025-07721-9 SHARE THIS ARTICLE Anyone you share the following link

with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative