Time-domain photonic image processor based on speckle projection and reservoir computing
- Select a language for the TTS:
- UK English Female
- UK English Male
- US English Female
- US English Male
- Australian Female
- Australian Male
- Language selected: (auto detect) - EN
Play all audios:

ABSTRACT High-speed image processing is essential for many real-time applications. On-chip photonic neural network processors have the potential to speed up image processing, but their
scalability is limited in terms of the number of input/output channels because high-density integration is challenging. Here, we propose a photonic time-domain image processing approach,
where real-world visual information is compressively acquired through a single input channel. Thus, large-scale processing is enabled even when using a small photonic processor with limited
input/output channels. The drawback of the time-domain serial operation can be mitigated using ultrahigh-speed data acquisition based on gigahertz-rate speckle projection. We combine it with
a photonic reservoir computer and demonstrate that this approach is capable of dynamic image recognition at gigahertz rates. Furthermore, we demonstrate that this approach can also be used
for high-speed learning-based imaging. The proposed approach can be extended to diverse applications, including target tracking, flow cytometry, and imaging of sub-nanosecond phenomena.
SIMILAR CONTENT BEING VIEWED BY OTHERS LARGE-SCALE PHOTONIC COMPUTING WITH NONLINEAR DISORDERED MEDIA Article 14 June 2024 PHOTONIC SIGNAL PROCESSOR BASED ON A KERR MICROCOMB FOR REAL-TIME
VIDEO IMAGE PROCESSING Article Open access 20 December 2023 ULTRAFAST SILICON PHOTONIC RESERVOIR COMPUTING ENGINE DELIVERING OVER 200 TOPS Article Open access 30 December 2024 INTRODUCTION
Rapid advances in information technologies, particularly in fields such as machine learning, have generated an escalating demand for innovative computing hardware and
concepts1,2,3,4,5,6,7,8,9,10,11,12. Among them, photonic computing has attracted considerable attention owing to recent developments in photonic integration and optical communication
technologies6,13,14,15,16,17,18,19. Recent studies have revealed the potential for overcoming major bottlenecks in electronic computing, suggesting that ultrahigh-speed computing with low
energy consumption can be achieved16,20,21. Photonic computing substrates have been predominantly used to process optical analog signals and play an essential role in the interface between
the physical world and the digital domain18,22. Such photonic approaches hold promise for accelerating signal preprocessing from sensing units, thereby alleviating the computational burden
typically borne by electronic postprocessing units. However, when photonic processing units handle signals acquired by sensing devices, the overall processing speed is essentially limited by
the data acquisition speed of the sensing devices and the transfer to the processing units. This limitation becomes particularly severe when image sensors with numerous pixels are employed.
In such systems, the spatial information acquired by an image sensor is converted into the electrical domain in a digital format, and large amounts of memory are required for data storage.
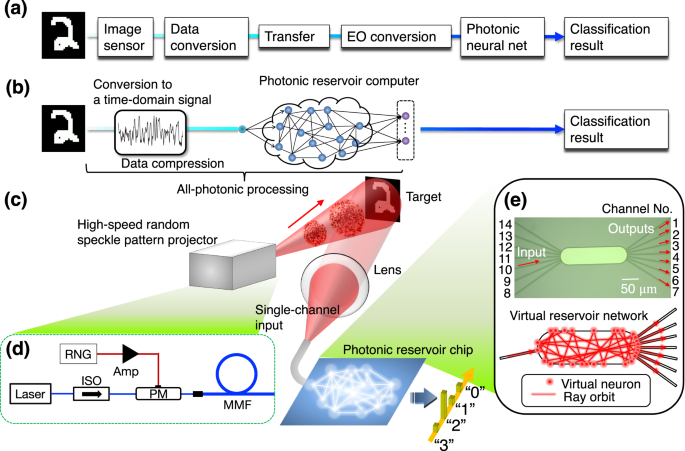
The electrical domain conversion and memory accesses required for large amounts of data are significant bottlenecks that hinder the speed of image processing (Fig. 1a). Photonic neural
network processors have great potential for accelerating image processing14,16,22,23,24,25,26,27. Some of these processors enable direct image acquisition without the use of image sensors
and subsequent optical processing14,22,23. In particular, on-chip photonic neural networks offer the promise of ultralow latency processing23 but usually suffer from physical size
constraints arising from the difficulty of high-density photonic integration. The maximum number of input/output nodes (channels) implemented in a photonic chip is limited, and such a size
constraint makes scalable operation difficult. Here, we introduce a scalable photonic image processing approach that circumvents the physical size constraints by exploiting the temporal
degrees of freedom of photons. In our approach, visual information from physical objects can be compressively acquired with only a _single_ input channel and can be optically processed in
the time domain. Consequently, the time-domain approach does not require many input/output channels and facilitates large-scale photonic processing. A pivotal technique underpinning
time-domain processing is the photonic domain transformation from the spatial-domain information of a physical object into a time-domain signal using an optical random pattern projection.
Similar techniques have been previously employed for ghost imaging or single-pixel imaging28,29. Single-pixel-based techniques typically require multiple measurements using different mask
patterns and suffer from low switching rates of the mask patterns, typically ranging from tens of Hz to tens of MHz30,31,32,33. Consequently, the acquisition of such image information is
time-consuming. To address this limitation, we use a high-speed random mask pattern projector based on dynamic speckle generation34 and show that it allows random mask patterns to be
switched at a rate of tens of GHz, which is at least three orders of magnitude higher than that of conventional approaches. In this study, the image-encoded optical signals are directly sent
to a photonic reservoir computer (Fig. 1b). A feature of reservoir computing (RC) is that it can achieve excellent inference performance in time-series processing with a simple training
method35,36,37,38,39,40,41,42. We use a microcavity-based RC for processing the time-domain signals and experimentally demonstrate that this approach is capable of high optical compression
of the image information and dynamic image recognition. This approach works even when using the RC with only a limited number of input/output channels and enables high-speed image
recognition and anomaly detection at gigahertz rates. By using a wavelength-multiplexing technique that provides parallel processing, we can further accelerate data acquisition and
processing. Beyond image recognition, our approach also serves as a compressive temporal encoder for single-shot high-speed imaging. This encoder enables continuous acquisition of a dynamic
scene at GHz rates, combined with various techniques developed for high-speed optical fiber communication, including optical multiplexing techniques. The number of frames of captured images
is not limited, in contrast to other high-speed imaging techniques based on pulse lasers and/or streak cameras43,44,45,46. A related imaging technique is optical time-stretching
imaging47,48, which is based on the optical encoding of images in individual laser pulses and has been used for the imaging of fast-moving objects. State-of-the-art time-stretching imaging,
when combined with structured light and compressive sensing techniques, has achieved frame rates ranging from megahertz to gigahertz levels49,50 and efficient data compression51. A feature
of our image encoding technique is that it does not rely on an ultrashort laser pulse source but a commercial continuous-wave laser, unlike time-stretching imaging. Thus, our technique
enables continuous imaging with a flexible time resolution and can achieve a higher frame rate using wavelength-division multiplexing. In this study, we experimentally demonstrate the
imaging of a transient phenomenon at a microsecond scale. RESULTS BASIC OPERATION PRINCIPLE The proposed system architecture includes a random pattern projector to temporally encode the
spatial information of the target objects and a photonic RC processor to process image-encoded time-domain signals (Fig. 1c). The random pattern projector generates random mask patterns,
which are projected onto the target object. The light reflected from the target is focused by a focusing lens and directly sent to the photonic RC processor, where an image of the target is
denoted by _v_(_x_, _y_), and (_x_, _y_) represents the coordinates on the image plane. For a random mask pattern Mask(_x_, _y_, _t_) on the image plane at time _t_, the input light _u_(_t_)
to the RC processor can be characterized by the spatial integral ∫Mask(_x_, _y_, _t_)_v_(_x_, _y_)_d__x__d__y_, that is, the spatial information of the target image is encoded as a
time-domain signal. The reservoir plays a role in mapping the input _u_(_t_) into a high-dimensional feature space7; thus, the features of _u_(_t_) can be separately distributed in the
high-dimensional space, resulting in better recognition by simple postprocessing. Let _X__r_(_t_) and \(\phi ({{{{{{{{\boldsymbol{x}}}}}}}}}_{r}(t))\in {{\mathbb{R}}}^{M}\) be the
reservoir’s internal state vector and observables in response to _u_(_t_). The observables _ϕ_(_X__r_(_t_)) are sampled at sampling time interval _τ__s_ during acquisition time _T__N_.
Similarly to previous studies42, the output vector \({{{{{{{\boldsymbol{y}}}}}}}}(n)\in {{\mathbb{R}}}^{{M}_{y}}(n\in \{1,2,\cdots \,\})\) is given by the observables _ϕ_(_X__r_(_t__n__j_)),
readout weights \({{{{{{{{\boldsymbol{W}}}}}}}}}_{j}\in {{\mathbb{R}}}^{{M}_{y}\times M}\), and bias \({{{{{{{\boldsymbol{b}}}}}}}}\in {{\mathbb{R}}}^{{M}_{y}}\) as
\({{{{{{{\boldsymbol{y}}}}}}}}(n)=\mathop{\sum }\nolimits_{j = 0}^{N-1}{{{{{{{{\boldsymbol{W}}}}}}}}}_{j}\phi ({{{{{{{{\boldsymbol{x}}}}}}}}}_{r}({t}_{nj}))+{{{{{{{\boldsymbol{b}}}}}}}}\)
for regression tasks, where _t__n__j_ = _n__T__N_ + _j__τ__s_, (_j_ ∈ {0, 1, ⋯ , _N_ − 1}) and _N_ = _T__N_/_τ__s_, and _Y_(_n_) = _f_(∑_j__W__j__ϕ_(_X__r_(_t__n__j_)) + _B_) for
classification tasks, where _f_ is a softmax function. In this scheme, the output vector _Y_(_n_) can be obtained in time interval _T__N_. The weight matrix _W__j_ can be trained using a
training dataset such that a loss function, which is characterized by the difference between the output vector _Y_(_n_) and the target vector _Y_tag(_n_), is minimized. RC can quickly
determine the global minimum of the loss function, resulting in low training costs. Postprocessing can be performed with application-specific circuits or field-programmable gate arrays for
low-latency operation. In this study, we focused on evaluating the ability of an RC processor in terms of fast data acquisition and preprocessing as a proof of concept. HIGH-SPEED RANDOM
PATTERN PROJECTOR The random pattern projector is based on a high-speed speckle generator, which is composed mainly of a laser source, deterministic random number generator, phase modulator,
and multimode fiber (MMF) (Fig. 1d). When coherent light is input into the MMF, it couples into multiple propagation modes with different phase velocities, and their interference produces a
speckle pattern at the end face of the MMF52. These speckles are highly sensitive to changes in the phase of the incident light. Therefore, by dynamically modulating the phase of the
incoming light, we can alter the speckle patterns, which serve as the mask patterns for projection. In previous studies, spatial light modulators (SLMs) such as digital micromirror devices
(DMDs) have been utilized to generate optical mask patterns at rates of up to 22 kHz28. A recent promising study demonstrated modulation rates up to 2.4 MHz using mechanically rotating mask
patterns30. In contrast, our proposed projector can attain modulation rates exceeding tens of gigahertz using a wideband phase modulator. (We used a 16-GHz phase modulator in this study.)
PHOTONIC RESERVOIR COMPUTING PROCESSOR A major advantage of using a photonic RC processor is that the high-dimensional mapping operation, resulting in better inference, can be optically
performed at low latency and high speed. We designed and fabricated a silicon photonic chip based on a stadium-shaped microcavity structure coupled to 14 single-mode waveguides (Fig. 1e).
The microcavity acts as a reservoir, whereas the single-mode waveguides are used as the input/output channels to and from the reservoir. A feature of the microcavity is its efficient
capability for optical confinement in a small footprint and the formation of various wave patterns depending on the shape of the microcavity53. The stadium-shaped cavity is known to be a
ray-chaotic cavity and is inspired by the Bunimovich stadium54. The wave mixing due to the chaotic nature of the cavity forms a wave field inside the cavity corresponding to a spatially
continuous optical random network within 50 _μ_m × 200 _μ_m (Fig. 1e). The length of the memory for storing past information was roughly estimated as 0.25 ns, partially with the aid of the
time-delay caused by the length difference in the optical fibers coupled to the output ports from the stadium cavity (see Supplementary Note 1.) Nonlinearity is introduced in the intensity
detection. Numerical results reveal that the stadium-shaped cavity-based RC has a higher computational performance for tasks requiring nonlinearity than nonchaotic cavity-based RC55,
although the cavity parameters used in the study are different from the present study. Other studies have also revealed the potential of ray-chaotic cavities, such as the stadium-shaped
cavity, as reservoirs numerically56 or with a microwave experiment57. To our knowledge, this study reports the first experimental demonstration of photonic microcavity-based RC for image
processing. For a description of the fundamental capabilities of temporal signal processing, see Supplementary Note 1 and Supplementary Figs. 1–3, where it is shown that the photonic RC
processor can outperform photonic RC systems or a photonic neural network circuit on benchmark datasets. IMAGE RECOGNITION We evaluated the image recognition performance of the proposed
system. In the experiment, we chose 28 × 28-pixel MNIST handwritten digit images58 from “0” to “3” as the target images and displayed them on a DMD (Fig. 2a). Random speckle patterns were
generated and projected onto the target at a rate of 25 Gigasamples per seconds (GS/s). The reflected light was introduced into the photonic RC processor via an optical fiber. The RC outputs
were measured using fast-response photodetectors. Figure 2b, c shows the change over time in the light intensity reflected from the images of the targets (i.e., an input to the RC) and the
corresponding RC outputs from channels 2–6 (Fig. 1e), respectively. The waveforms of the reflected light strongly depended on the images of the targets, and a variety of spatiotemporal
responses in the reservoir outputs were produced. For the evaluation, we used 1000 samples of images of digits from “0” to “3” and acquired the RC outputs over acquisition time _T__N_ for
each image. The prediction outputs _Y_ were trained on 900 image samples and tested on 100 image samples. To characterize how much information of the target image is compressively input to
the RC processor during the acquisition time _T__N_, we defined the compressive sensing ratio _C_ of the image-encoded signal input to the RC processor as _N_/(28 × 28)59, where _N_ =
_T__N_/_τ__s_ denotes the number of data points of the image-encoded time-domain signal. Figure 3a shows the classification accuracy for various acquisition times and compressive sensing
ratios. The classification accuracy exceeded 90% for _T__N_ ≥ 0.4 ns, which corresponds to the compressive sensing ratio _C_ ≥ 1.28%, revealing the potential of the proposed approach for
ultrafast image recognition at sub-nanoseconds with a substantial compression efficiency. As an example, the confusion matrix for _T__N_ = 0.56 ns (_C_ = 1.78%) is shown in Fig. 3b. Most
predicted labels were distributed along the diagonal line and matched the true labels. For comparison, we also performed numerical simulations. To mimic the random projection of a digit
image (28 × 28 = 784 pixels in size), an _N_ × 784 Gaussian random mask matrix was used. As a classifier, we used a neural network with a single fully connected hidden layer and \(\tanh\)
activation functions. We confirmed that the classification performance of the proposed system was comparable to that of the neural network (Fig. 3a). To gain insights into the effect of the
photonic RC processor, we investigated the classification performance of the system without the RC processor, where the time-domain signal before RC processing was directly used as an input
to a linear classifier. The classification performance was found to be substantially worse than that of the system proposed in this study (Fig. 3c). The photonic RC processor has a finite
memory time (Supplementary Fig. 4). The memory time can partly contribute to storing and mixing the image-encoded time-domain information during the acquisition time _T__N_ of
sub-nanoseconds. The memory and high-dimensional mapping operation of the RC can result in better classification. We also evaluated the classification performance on larger and more
difficult image datasets. Image classification was successfully performed even for such datasets with high compressive efficiency at nanosecond acquisition times. See Supplementary Note 2
and Supplementary Figs. 5 and 6 for details. RECOGNIZING MICROSECOND PHENOMENA To demonstrate the capability of recognizing dynamic scenes, we measured the switching behavior of the DMD,
which switched between displaying digit “1” and digit “2” images. In the experiment, the laser light was repeatedly phase-modulated using the same pseudorandom signal, and the dynamic
speckle patterns were repeatedly projected onto the DMD. The reflected light was directed to our RC processor, and the reservoir outputs were acquired at _T__N_ = 0.56 ns to obtain the
classification results. According to our correlation analysis, the digit “1” image transitioned to the digit “2” image around 4600 ns (Fig. 4a). Figure 4b shows the time dependence of the
classification probability for the switching behavior. The result reveals that the digit “1” image was switched to that of digit “2” around 4600 ns, and digit “2” can be steadily recognized
after the transition (see Supplementary Movie 1). The detection of the switching behavior was consistent with the results of our correlation analysis. Although the time scale of the DMD
display switching was on the order of a few microseconds, our system has the potential to recognize and detect faster phenomena. IMAGE-FREE ANOMALY DETECTION Next, we evaluated the
feasibility of anomaly detection (Fig. 5a). Anomaly detection is the task of identifying an abnormality or rare event from sampled information and must operate in real-time as much as
possible. Detecting anomalies using images generally requires heavy computation, which prevents real-time operation. This problem becomes more serious when the implementation of an edge
device with limited computational resources is considered. Our photonic approach can reduce redundant and unnecessary information in the image data through a compressive transformation into
time series data; thus, the required computation for detection can be offloaded from the electronic postprocessing units. This approach also provides the advantage that image data can be
treated in the same manner as time series data from other sensors. The lightweight computation and low training cost of our approach enable not only on-device prediction but also on-device
learning in edge devices. To demonstrate this, we used a benchmark dataset of concrete cracks for structural health monitoring and inspections60,61. The dataset contains 227 × 227-pixel
concrete images with and without cracks. Each image was taken approximately 1 m away from the surface with a camera directly facing the target61. The images were displayed on the DMD. The
system was trained with 1500 normal image samples (without cracks) such that the output _y_ corresponded to a constant value _α_ = 1. To identify abnormalities (images with cracks in this
case), an anomaly score was defined as the representation error (_y_ − _α_)2. This score is distributed around zero for normal images (without cracks), whereas it has a large outlier when a
crack is detected (Fig. 5b). The receiver operating characteristic (ROC) curve, which plots true positive rates against the false positive rates, is shown in Fig. 5c. The area under the
curve (AUC) was 0.974, which suggests a good measure of separability, considering AUC = 1 in an ideal model. HIGH-SPEED IMAGE ENCODER FOR IMAGE RECONSTRUCTION Here, we demonstrate that the
proposed system can be used not only as a high-speed recognizer but also as a high-speed imager (Fig. 6a). A key advantage of our proposed system is that the reservoir outputs include the
image information; thus, an image can be reconstructed from the reservoir outputs using appropriate reconstruction algorithms, e.g., well-developed algorithms for ghost imaging and
single-pixel imaging28. However, such algorithms require complete information on the sequences of the projected random mask patterns, which is not applicable in our case because it is
difficult to measure the fast spatiotemporal behavior of random patterns over 10 GHz rates with an image sensor, which typically operates at tens of hertz. Therefore, we used a trained
neural network model to reconstruct the image of a target from the measured reservoir outputs (Fig. 6a). Note that real-time processing is not required for this reconstruction. As a simple
proof-of-concept experiment, we used two original datasets containing four-class handwritten digit images and four-class images from the Fashion-MNIST dataset62. Each image was binarized and
displayed on the DMD, and reservoir outputs were recorded for _T__N_ = 20 ns. To reconstruct the image, we used a convolutional neural network model trained to output the corresponding
target image. We used 900 images for training and 100 images for testing. Figure 6b shows the results of image reconstruction for some of the test samples. The root mean squared error (RMSE)
values for the 100 test images were 0.219 and 0.223 for the MNIST handwritten digit and Fashion-MNIST datasets, respectively. Decreasing _T__N_ led to an increase in the RMSE. However, this
trade-off can be resolved by incorporating wavelength-division multiplexing (WDM). A similar performance was obtained for _T__N_ ≥ 0.8 ns in the WDM scheme. See Supplementary Note 3 and
Supplementary Figs. 7 and 8 for details. The proposed encoder facilitates the observation of a rare event or transient phenomenon. The proposed approach does not require broadband pulse
lasers for the encoding of the target images. Continuous recording over a long period with a controllable time resolution _T__N_ is feasible. To evaluate the feasibility of continuous
recording as a primitive experiment, we reconstructed images of the microsecond switching behavior when the DMD switched from displaying digit “1” image to displaying digit “2” image. In
this experiment, the dynamic speckle patterns were repeatedly projected onto the DMD, and the reservoir outputs were acquired using _T__N_ = 20 ns. Under these conditions, the image at each
timestep can be reconstructed with a time resolution of _T__N_ (see Supplementary Movie 1). As shown in Fig. 6c, the switching from digit “1” to “2” can be observed. However, because the
network was trained only with four classes of digit images in this study, the reconstructed transient images (shown in the middle of Fig. 6c) might not be captured correctly; the images can
be attributed only to the projections of the digit images used in training. For more precise image reconstruction, it is advisable to train the reconstruction model using a more extensive
dataset comprising independent basis images, such as Hadamard basis patterns63. DISCUSSION We proposed and experimentally demonstrated a high-speed photonic time-domain image processing
approach. This photonic approach is totally different from previous time-domain processing approaches, which involve electronic preprocessing of input image data16,64. In our approach,
real-world visual information is highly compressed and optically acquired through a single input channel. This feature empowers optical high-speed time-domain processing at gigahertz rates
even when using a small optical processor with a limited number of input/output channels. This approach is scalable, versatile, has a low training computational cost, and is suitable for
deployment in edge-computing devices. Moreover, this approach leverages the advantages elucidated in previous studies on ghost imaging or single-pixel imaging, such as robustness to noise
and the capability to process images under extremely low-light conditions. The processing rate can be further increased through refinements and improvements. A potential approach is to use
parallel processing based on multiplexing techniques such as space-division multiplexing and/or WDM. A space-division multiplexing technique could be implemented using multiple fiber
receivers in the proposed system. For WDM, a multi-wavelength laser (e.g., an optical comb) would enable the generation of independent speckle patterns in parallel. The approach can lead to
a significant reduction in the acquisition time of a target image without decreasing classification accuracy (See Supplementary Fig. 7). Despite the advantages of the proposed approach,
there is room for further improvement. One improvement is to make the proposed fiber system more robust because speckle patterns are sensitive to environmental changes, such as vibrations
and temperature fluctuations. The recognition accuracy degraded under a temperature fluctuation of ±0. 3 °C (Supplementary Note 4). However, the system stability can be improved in terms of
both hardware and software by isolating the MMF from environmental temperature fluctuations and/or by training the optimal weight parameters of the neural network with data samples acquired
at different temperatures (see Supplementary Fig. 9). The second is to improve the photonic RC processor, which has only a short memory and linear operation. The memory time can be improved
with larger-sized cavities designed for a higher quality factor, e.g., photonic crystal cavities56. In our setup, a nonlinear component, e.g., a semiconductor optical amplifier with strong
gain saturation, can be easily introduced to add a nonlinear conversion in the image-encoded signal before the reservoir processing. The proposed time-domain image acquisition approach is
applicable to various time-domain processors, including recurrent neural networks, delay-based reservoir computers65, and extreme learning machines66. The third is to develop a postprocessor
to realize a fast end-to-end photonic processor. One approach to accomplish this is to deploy a photonic postprocessing technique developed as an analog readout in RC. This technique is
based on a balanced Mach–Zehnder modulator and an integrator67 so that the multiply-accumulation operation can be performed in the time domain. An additional advantage of analog computation
in the time domain is that it can be performed even at ultra-low energies; in principle, a weak signal at a single-photon level can be processed11. We also demonstrated that the proposed
approach can be used for high-speed imaging. The proposed approach is simple, versatile, and can continuously record a target scene for a long time. A wide range of time-scale phenomena can
be captured by varying the modulation rate and controlling the acquisition time. Another feature of this approach is its compatibility with optical multiplexing techniques, such as WDM. This
can compensate for a drawback of the time-domain approach, i.e., the trade-off between the resolution of the acquired images and acquisition time. By incorporating the WDM, image
acquisition can be achieved in a shorter time scale by suppressing the degradation of the image resolution (Supplementary Fig. 8), which can open a novel pathway for the imaging of ultrafast
dynamic phenomena. METHODS EXPERIMENTAL SETUP In our random speckle pattern projector, a narrow-linewidth tunable laser (Alnair Labs, TLG-220, linewidth < 100 kHz, 30 mW) was used as a
coherent light source. The laser wavelength was set as 1550 nm. To dynamically generate speckle patterns, the laser light was phase-modulated using a lithium niobate phase modulator (EO
Space, PM-5S5-20-PFA-PFA-UV-UL, 16 GHz bandwidth) with a uniformly distributed pseudorandom sequence generated using an arbitrary waveform generator (Tektronix, AWG70002A, 25 GS/s). The
modulated light was directed through a polarization-maintaining single-mode fiber to the MMF, which is a commercially available step-index MMF with a core diameter of 200 μm, numerical
aperture (NA) of 0.39, and length of 20 m. The light reflected from the DMD was collected using a focusing lens coupled to an MMF with a core diameter of 50 μm. Using the MMF facilitates
straightforward coupling with the reflected light and introduces an additional mixing effect for the time-domain signal. The fiber was connected to an Erbium-doped fiber amplifier (Thorlabs,
EDFA100P) and directed to the photonic RC processor. The output signals were amplified with EDFAs and measured using photodetectors (New Port, 1554-B). We set the number of the output
signals as _M_ = 5 for 4-class recognition tasks and an anomaly detection task. To evaluate performance, the signals were digitized using a digital oscilloscope (Tektronix, DPO72504DX, 25
GHz bandwidth) with _τ__s_ = 0.04 ns and postprocessed using a computer. PHOTONIC RC PROCESSOR The RC processor was fabricated on a silicon chip. A 220 nm thick silicon layer was etched to
form a stadium-shaped microcavity coupled with 14 single-mode waveguides. The single-mode waveguides were used as the input and output channels. The stadium was shaped with two semicircles
of radius 25 μm and two parallel segments of length 150 μm. The width of the single-mode waveguide was 500 nm. A spot-size converter was used to couple the single-mode waveguide and an
optical fiber. The variation in the fiber lengths coupled to the output ports of the photonic chip creates an additional time-delay memory for the input information. It partly contributes to
the memory capacity of the whole RC system (Supplementary Note 1). COMPENSATION FOR OPTICAL LOSSES The optical losses in the receiver and processing section were mainly caused by the
coupling losses of the receiver fiber, the coupling loss between the receiver fiber and a single-mode waveguide in a photonic chip, and the scattering loss in the microcavity, which were
estimated as 8.8 dB, 17 dB, and more than 15 dB, respectively. The large losses were optically compensated using EDFAs with a noise figure of less than 5 dB. The signals were amplified with
a gain from 25 dB to 30 dB so that the power was less than the saturation power of the photodetectors. The signal-to-noise ratio was estimated to range from 12.5 dB to 14 dB. In the range,
the recognition performance was not significantly changed. The coupling loss can be mitigated by employing a mode converter to minimize mode mismatch, while the scattering loss can be
reduced by designing a high-Q cavity, such as a photonic crystal cavity56. POSTPROCESSING FOR IMAGE RECOGNITION The reservoir outputs were detected at a sampling time interval of _τ__s_
during acquisition time _T__N_. For the _M_ reservoir outputs with a record length of _N_ = _T__N_/_τ__s_, _M__N_ features were used as inputs of the (linear) softmax classifier. The
classifier was trained using Python (scikit-learn package) on a computer (OS: Mac, Chip: Apple M1 Max, Cores: 8, Memory: 64 GB). The computation time was a few seconds and a few ten seconds
for the four-class and ten-class image recognition tasks, respectively. IMAGE RECONSTRUCTION In the image reconstruction task, we used the reservoir outputs from channels 2–6 (_M_ = 5),
which were sampled at intervals of _τ__s_ = 40 ps. During preprocessing, the reservoir outputs were normalized using their respective means and standard deviations. The number of sampled
data points for each reservoir output was _N_ = _T__N_/_τ__s_; thus, _M__N_ sampled data points were used as the input to the neural network model for image reconstruction. (_T__N_ ranged
from 0.2 ns to 20 ns.) In the network model used to obtain the results shown in Fig. 6b, a fully connected network of size _M__N_ × 200 was used in the first layer. The outputs were sent to
the first one-dimensional (1D) CNN layer with 10 kernels of size 3 and the ReLU activation function, followed by batch normalization and max pooling of size 2 × 2. The second 1D CNN layer
used a single kernel of size 3 and the ReLU function, followed by batch normalization and max pooling of size 2 × 2. Then, in the fourth and fifth layers, fully connected networks of 50 ×
784 and 784 × 784 were used to output the 28 × 28-pixel image. The network model was trained with _K_ = 900 image samples to minimize the mean squared error, which can be expressed as
follows: \(E=(1/K)\mathop{\sum }\nolimits_{k}^{K}{\sum }_{i,j}{({I}_{k}(i,j)-{I}_{k}^{({{{{\rm{target}}}}})}(i,j))}^{2}\), where _I__k_(_i_, _j_) and \({I}_{k}^{({{{{\rm{target}}}}})}(i,j)\)
denote the pixel values of the reconstructed image and target image in the _i_th row and _j_th column for the _k_th sample, respectively. Subsequently, the model was tested with a separate
set of 100 image samples. DATA AVAILABILITY The data that support the findings of this study are available from the corresponding author upon reasonable request. The three public image
datasets used in this study are available at the following locations: (1) MNIST: http://yann.lecun.com/exdb/mnist/; (2) Fashion-MNIST: https://github.com/zalandoresearch/fashion-mnist; (3)
Concrete Crack: https://data.mendeley.com/datasets/5y9wdsg2zt/1. CODE AVAILABILITY The codes that support the findings of this study are available from the corresponding author upon
reasonable request. REFERENCES * Carleo, G. et al. Machine learning and the physical sciences. _Rev. Mod. Phys._ 91, 045002 (2019). ADS Google Scholar * Merolla, P. A. et al. A million
spiking-neuron integrated circuit with a scalable communication network and interface. _Science_ 345, 668–673 (2014). ADS Google Scholar * Grollier, J. et al. Neuromorphic spintronics.
_Nat. Electron._ 3, 360–370 (2020). Google Scholar * Marković, D., Mizrahi, A., Querlioz, D. & Grollier, J. Physics for neuromorphic computing. _Nat. Rev. Phys._ 2, 499–510 (2020).
Google Scholar * Bogaerts, W. & Rahim, A. Programmable photonics: an opportunity for an accessible large-volume pic ecosystem. _IEEE J. Sel. Top. Quantum Electron._ 26, 1–17 (2020).
Google Scholar * Shastri, B. J. et al. Photonics for artificial intelligence and neuromorphic computing. _Nat. Photonics_ 15, 102–114 (2021). ADS Google Scholar * Tanaka, G. et al. Recent
advances in physical reservoir computing: a review. _Neural Netw._ 115, 100–123 (2019). Google Scholar * Furuhata, G., Niiyama, T. & Sunada, S. Physical deep learning based on optimal
control of dynamical systems. _Phys. Rev. Appl._ 15, 034092 (2021). ADS Google Scholar * Wright, L. G. et al. Deep physical neural networks trained with backpropagation. _Nature_ 601,
549–555 (2022). ADS Google Scholar * Nakajima, M. et al. Physical deep learning with biologically inspired training method: gradient-free approach for physical hardware. _Nat. Commun._ 13,
7847 (2022). ADS Google Scholar * Sludds, A. et al. Delocalized photonic deep learning on the internet’s edge. _Science_ 378, 270–276 (2022). ADS Google Scholar * Hughes, T. W.,
Williamson, I. A. D., Minkov, M. & Fan, S. Wave physics as an analog recurrent neural network. _Sci. Adv._ 5, eaay6946 (2019). ADS Google Scholar * Tait, A. N. et al. Neuromorphic
photonic networks using silicon photonic weight banks. _Sci. Rep._ 7, 7430 (2017). ADS Google Scholar * Lin, X. et al. All-optical machine learning using diffractive deep neural networks.
_Science_ 361, 1004–1008 (2018). ADS MathSciNet MATH Google Scholar * Sui, X., Wu, Q., Liu, J., Chen, Q. & Gu, G. A review of optical neural networks. _IEEE Access_ 8, 70773–70783
(2020). Google Scholar * Feldmann, J. et al. Parallel convolutional processing using an integrated photonic tensor core. _Nature_ 589, 52–58 (2021). ADS Google Scholar * Xu, X. et al. 11
tops photonic convolutional accelerator for optical neural networks. _Nature_ 589, 44–51 (2021). ADS Google Scholar * Kitayama, K. et al. Novel frontier of photonics for data
processing—photonic accelerator. _APL Photonics_ 4, 090901 (2019). ADS Google Scholar * Shen, Y. et al. Deep learning with coherent nanophotonic circuits. _Nat. Photonics_ 11, 441–446
(2017). ADS Google Scholar * Hamerly, R., Bernstein, L., Sludds, A., Soljačić, M. & Englund, D. Large-scale optical neural networks based on photoelectric multiplication. _Phys. Rev.
X_ 9, 021032 (2019). Google Scholar * Wang, T. et al. An optical neural network using less than 1 photon per multiplication. _Nat. Commun._ 13, 123 (2022). ADS Google Scholar * Wang, T.
et al. Image sensing with multilayer nonlinear optical neural networks. _Nat. Photonics_ 17, 408–415 (2023). ADS Google Scholar * Ashtiani, F., Geers, A. J. & Aflatouni, F. An on-chip
photonic deep neural network for image classification. _Nature_ 606, 501–506 (2022). ADS Google Scholar * Shi, W. et al. Loen: Lensless opto-electronic neural network empowered machine
vision. _Light_ 11, 121 (2022). Google Scholar * Chang, J., Sitzmann, V., Dun, X., Heidrich, W. & Wetzstein, G. Hybrid optical-electronic convolutional neural networks with optimized
diffractive optics for image classification. _Sci. Rep._ 8, 12324 (2018). ADS Google Scholar * Mennel, L. et al. Ultrafast machine vision with 2D material neural network image sensors.
_Nature_ 579, 62–66 (2020). ADS Google Scholar * Antonik, P., Marsal, N., Brunner, D. & Rontani, D. Human action recognition with a large-scale brain-inspired photonic computer. _Nat.
Mach. Intell._ 1, 530–537 (2019). Google Scholar * Gibson, G. M., Johnson, S. D. & Padgett, M. J. Single-pixel imaging 12 years on: a review. _Opt. Express_ 28, 28190–28208 (2020). ADS
Google Scholar * Bromberg, Y., Katz, O. & Silberberg, Y. Ghost imaging with a single detector. _Phys. Rev. A_ 79, 053840 (2009). ADS Google Scholar * Hahamovich, E., Monin, S.,
Hazan, Y. & Rosenthal, A. Single pixel imaging at megahertz switching rates via cyclic hadamard masks. _Nat. Commun._ 12, 4516 (2021). ADS Google Scholar * Xu, Z.-H., Chen, W.,
Penuelas, J., Padgett, M. & Sun, M.-J. 1000 fps computational ghost imaging using led-based structured illumination. _Opt. Express_ 26, 2427–2434 (2018). ADS Google Scholar * Shi, W.,
Hu, C., Yang, S., Chen, M. & Chen, H. Optical random speckle encoding based on hybrid wavelength and phase modulation. _Opt. Lett._ 46, 3745–3748 (2021). ADS Google Scholar * Wang, Y.
et al. High speed computational ghost imaging via spatial sweeping. _Sci. Rep._ 7, 45325 (2017). ADS Google Scholar * Hanawa, J., Niiyama, T., Endo, Y. & Sunada, S. Gigahertz-rate
random speckle projection for high-speed single-pixel image classification. _Opt. Express_ 30, 22911–22921 (2022). ADS Google Scholar * Jaeger, H. & Haas, H. Harnessing nonlinearity:
predicting chaotic systems and saving energy in wireless communication. _Science_ 304, 78–80 (2004). ADS Google Scholar * Verstraeten, D., Schrauwen, B., D’Haene, M. & Stroobandt, D.
An experimental unification of reservoir computing methods. _Neural Netw._ 20, 391–403 (2007). MATH Google Scholar * Van der Sande, G., Brunner, D. & Soriano, M. C. Advances in
photonic reservoir computing. _Nanophotonics_ 6, 561–576 (2017). Google Scholar * Paquot, Y. et al. Optoelectronic reservoir computing. _Sci. Rep._ 2, 287 (2012). Google Scholar *
Vandoorne, K. et al. Experimental demonstration of reservoir computing on a silicon photonics chip. _Nat. Commun._ 5, 3541 (2014). ADS Google Scholar * Larger, L. et al. High-speed
photonic reservoir computing using a time-delay-based architecture: Million words per second classification. _Phys. Rev. X_ 7, 011015 (2017). Google Scholar * Rafayelyan, M., Dong, J., Tan,
Y., Krzakala, F. & Gigan, S. Large-scale optical reservoir computing for spatiotemporal chaotic systems prediction. _Phys. Rev. X_ 10, 041037 (2020). Google Scholar * Sunada, S. &
Uchida, A. Photonic neural field on a silicon chip: large-scale, high-speed neuro-inspired computing and sensing. _Optica_ 8, 1388–1396 (2021). ADS Google Scholar * Gao, L., Liang, J., Li,
C. & Wang, L. V. Single-shot compressed ultrafast photography at one hundred billion frames per second. _Nature_ 516, 74–77 (2014). ADS Google Scholar * Wang, P., Liang, J. &
Wang, L. V. Single-shot ultrafast imaging attaining 70 trillion frames per second. _Nat. Commun._ 11, 2091 (2020). ADS Google Scholar * Li, J. et al. Spectrally encoded single-pixel
machine vision using diffractive networks. _Sci. Adv._ 7, eabd7690 (2021). ADS Google Scholar * Nakagawa, K. et al. Sequentially timed all-optical mapping photography (stamp). _Nat.
Photonics_ 8, 695–700 (2014). ADS Google Scholar * Goda, K., Tsia, K. K. & Jalali, B. Serial time-encoded amplified imaging for real-time observation of fast dynamic phenomena.
_Nature_ 458, 1145–1149 (2009). ADS Google Scholar * Goda, K. & Jalali, B. Dispersive Fourier transformation for fast continuous single-shot measurements. _Nat. Photonics_ 7, 102–112
(2013). ADS Google Scholar * Lei, C. et al. GHz optical time-stretch microscopy by compressive sensing. _IEEE Photonics J._ 9, 1–8 (2017). Google Scholar * Bosworth, B. T. et al.
High-speed flow microscopy using compressed sensing with ultrafast laser pulses. _Opt. Express_ 23, 10521–10532 (2015). ADS Google Scholar * Li, R. et al. All-optical
Fourier-domain-compressed time-stretch imaging with low-pass filtering. _ACS Photonics_ https://doi.org/10.1021/acsphotonics.2c01708 (2023). * Rawson, E. G., Goodman, J. W. & Norton, R.
E. Frequency dependence of modal noise in multimode optical fibers. _J. Opt. Soc. Am._ 70, 968–976 (1980). ADS Google Scholar * Cao, H. & Wiersig, J. Dielectric microcavities: Model
systems for wave chaos and non-hermitian physics. _Rev. Mod. Phys._ 87, 61–111 (2015). ADS MathSciNet Google Scholar * Bunimovich, L. A. On ergodic properties of certain billiards.
_Funct. Anal. Appl._ 8, 254–255 (1974). MathSciNet MATH Google Scholar * Sunada, S. & Uchida, A. Photonic reservoir computing based on nonlinear wave dynamics at microscale. _Sci.
Rep._ 9, 19078 (2019). ADS Google Scholar * Laporte, F., Katumba, A., Dambre, J. & Bienstman, P. Numerical demonstration of neuromorphic computing with photonic crystal cavities. _Opt.
Express_ 26, 7955–7964 (2018). ADS Google Scholar * Ma, S., Antonsen, T. M., Anlage, S. M. & Ott, E. Short-wavelength reverberant wave systems for physical realization of reservoir
computing. _Phys. Rev. Res._ 4, 023167 (2022). Google Scholar * LeCun, Y., Cortes, C. & Burges, C. J. C. The mnist database of handwritten digits. http://yann.lecun.com/exdb/mnist/. *
Bacca, J., Correa, C. V., Vargas, E., Castillo, S. & Arguello, H. Compressive classification from single pixel measurements via deep learning. In _2019 IEEE 29th International Workshop
on Machine Learning for Signal Processing (MLSP)_, 1–6 https://doi.org/10.1109/MLSP.2019.8918920 (2019). * Minhas, M. S. & Zelek, J. Anomaly detection in images. Preprint at _arXiv_
https://doi.org/10.48550/arXiv.1905.13147 (2019). * Özgenel, Ç. F. & Sorguç, A. G. Performance comparison of pretrained convolutional neural networks on crack detection in buildings. In
(ed Teizer, J.) _Proceedings of the 35th International Symposium on Automation and Robotics in Construction (ISARC)_, 693–700 (International Association for Automation and Robotics in
Construction (IAARC), Taipei, Taiwan, 2018) https://doi.org/10.22260/ISARC2018/0094. * Xiao, H., Rasul, K. & Vollgraf, R. Fashion-mnist: a novel image dataset for benchmarking machine
learning algorithms. Preprint at _arXiv_ https://doi.org/10.48550/arXiv.1708.07747 (2017). * Zhang, Z., Wang, X., Zheng, G. & Zhong, J. Hadamard single-pixel imaging versus Fourier
single-pixel imaging. _Opt. Express_ 25, 19619–19639 (2017). ADS Google Scholar * Robertson, J. et al. Ultrafast neuromorphic photonic image processing with a vcsel neuron. _Sci. Rep._ 12,
4874 (2022). ADS Google Scholar * Takano, K. et al. Compact reservoir computing with a photonic integrated circuit. _Opt. Express_ 26, 29424–29439 (2018). ADS Google Scholar * Ortín, S.
et al. A unified framework for reservoir computing and extreme learning machines based on a single time-delayed neuron. _Sci. Rep._ 5, 14945 (2015). ADS Google Scholar * Duport, F.,
Smerieri, A., Akrout, A., Haelterman, M. & Massar, S. Fully analogue photonic reservoir computer. _Sci. Rep._ 6, 22381 (2016). ADS Google Scholar Download references ACKNOWLEDGEMENTS
This work was partly supported by JST PRESTO (Grant No. JPMJPR19M4), JSPS KAKENHI (Grant Nos. JP19H00868, JP20H04255, and JP22H05198), and JKA promotion funds from KEIRIN RACE (Grant No.
2022M-208). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Graduate School of Natural Science and Technology, Kanazawa University, Kakuma-machi, Kanazawa, Ishikawa, 920-1192, Japan Tomoya
Yamaguchi & Kohei Arai * Faculty of Mechanical Engineering, Institute of Science and Engineering, Kanazawa University, Kakuma-machi, Kanazawa, Ishikawa, 920-1192, Japan Tomoaki Niiyama
& Satoshi Sunada * Department of Information and Computer Sciences, Saitama University, 255 Shimo-Okubo, Sakura-ku, Saitama City, Saitama, 338-8570, Japan Atsushi Uchida * Japan Science
and Technology Agency, PRESTO, 4-1-8 Honcho, Kawaguchi, Saitama, 332-0012, Japan Satoshi Sunada Authors * Tomoya Yamaguchi View author publications You can also search for this author
inPubMed Google Scholar * Kohei Arai View author publications You can also search for this author inPubMed Google Scholar * Tomoaki Niiyama View author publications You can also search for
this author inPubMed Google Scholar * Atsushi Uchida View author publications You can also search for this author inPubMed Google Scholar * Satoshi Sunada View author publications You can
also search for this author inPubMed Google Scholar CONTRIBUTIONS S.S. conceived the idea and directed the project. T.Y. and S.S. designed the experimental setup and performed the
experiments and numerical analysis. K.A. evaluated the performance of the RC circuit. S.S., T.N., and A.U. discussed and wrote the manuscript. All authors contributed to the preparation of
the manuscript. CORRESPONDING AUTHOR Correspondence to Satoshi Sunada. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION
: _Communications Physics_ thanks Kathy Lüdge and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL
INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE
SUPPLEMENTARY INFORMATION DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY MOVIE 1 RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons
Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original
author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the
article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use
is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit
http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yamaguchi, T., Arai, K., Niiyama, T. _et al._ Time-domain photonic image processor
based on speckle projection and reservoir computing. _Commun Phys_ 6, 250 (2023). https://doi.org/10.1038/s42005-023-01368-w Download citation * Received: 24 May 2023 * Accepted: 01
September 2023 * Published: 14 September 2023 * DOI: https://doi.org/10.1038/s42005-023-01368-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:
Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative