News Reader.info

ABSTRACT Fragment-based drug discovery has been an effective paradigm in early-stage drug development. An open challenge in this area is designing linkers between disconnected molecular

fragments of interest to obtain chemically relevant candidate drug molecules. In this work, we propose DiffLinker, an E(3)-equivariant three-dimensional conditional diffusion model for

molecular linker design. Given a set of disconnected fragments, our model places missing atoms in between and designs a molecule incorporating all the initial fragments. Unlike previous

approaches that are only able to connect pairs of molecular fragments, our method can link an arbitrary number of fragments. Additionally, the model automatically determines the number of

atoms in the linker and its attachment points to the input fragments. We demonstrate that DiffLinker outperforms other methods on the standard datasets, generating more diverse and

synthetically accessible molecules. We experimentally test our method in real-world applications, showing that it can successfully generate valid linkers conditioned on target protein

pockets. SIMILAR CONTENT BEING VIEWED BY OTHERS STRUCTURE-BASED DRUG DESIGN WITH EQUIVARIANT DIFFUSION MODELS Article Open access 09 December 2024 A DEEP GENERATIVE MODEL FOR MOLECULE

OPTIMIZATION VIA ONE FRAGMENT MODIFICATION Article 09 December 2021 DIGFRAG AS A DIGITAL FRAGMENTATION METHOD USED FOR ARTIFICIAL INTELLIGENCE-BASED DRUG DESIGN Article Open access 11

November 2024 MAIN The space of pharmacologically relevant molecules is estimated to exceed 1060 structures1, and searching in that space poses substantial challenges for drug design. A

successful approach to reduce the size of this space is to start from ‘fragments’, smaller molecular compounds that usually have no more than 20 heavy (non-hydrogen) atoms. This strategy is

known as fragment-based drug design (FBDD)2. Given a protein pocket (a site on the target protein that has suitable properties for ligand binding), computationally determining fragments that

interact with the pocket is a cheaper and more efficient alternative to experimental screening methods2. Once the relevant fragments have been identified and docked to the target protein,

it remains to combine them into a single connected chemical compound. As has been shown in various applications, including FBDD3, scaffold hopping (that is, discovery of structurally novel

compounds starting from a known active molecule by modifying its core)4 and proteolysis targeting chimera (PROTAC) design5, the geometries of the identified fragments are crucial for the

effective design of relevant and potent molecules. In addition, consideration of the structure of the protein pocket during the linker design process can remarkably improve the affinity of

the generated compound leads6. In this work, we address the problem of linking fragments placed in a three-dimensional (3D) context with the possibility of conditioning the design process to

the target protein pocket. Since we address several possible application scenarios, we note that the term ‘linker’ denotes any chemical matter that can connect starting molecular fragments

and does not relate to any aspects of the terminology specific for any of the discussed domains. Early computational methods for molecular linker design were based on database search and

physical simulations7, both of which are computationally intensive. Therefore, there is increasing interest in machine learning methods that can go beyond the available data and generate

diverse linkers more efficiently. Existing approaches are based either on syntactic pattern recognition8 or on autoregressive models9,10,11. While the former method operates solely on

SMILES12, the latter takes into account 3D positions and orientations of the input fragments, as this information is essential for designing valid and stable molecules in various

applications (see Supplementary Information for details). However, these methods are not equivariant with respect to the permutation of atoms and can only combine pairs of fragments.

Finally, to date, there is no computational method for molecular linker design that takes the target protein pocket into account. In this work, we introduce DiffLinker, a conditional

diffusion model that generates molecular linkers for a set of input fragments represented as a 3D atomic point cloud. First, our model generates the size of the prospective linker and then

samples initial linker atom types and positions from the normal distribution. Next, the linker atom types and coordinates are iteratively updated using a neural network that is conditioned

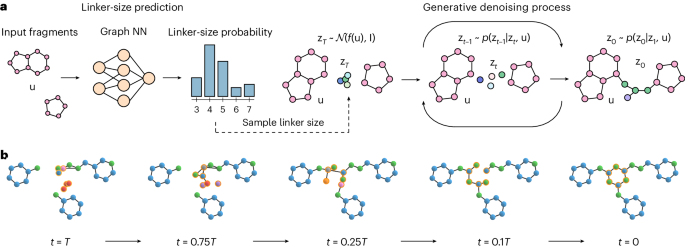
on the input fragments. Ultimately, the denoised linker atoms and the input fragment atoms form a single connected molecule, as shown in Fig. 1. DiffLinker has several desirable properties:

it is equivariant to translations, rotations, reflections and permutations; it is not limited by the number of input fragments, does not require information on the attachment atoms and

generates linkers with no predefined size. Moreover, we propose a new 3D conditioning mechanism for Euclidean diffusion models, which makes DiffLinker a versatile and state-of-the-art

generative method applicable to various structure-based drug design tasks. We show that DiffLinker has performance superior to that of previous methods in generating chemically relevant

linkers between pairs of fragments. Our method achieves state-of-the-art results in synthetic accessibility and drug-likeness, which makes it useful in drug design pipelines. Besides,

DiffLinker remarkably outperforms other methods in the chemical diversity of the generated linkers. We further propose a more challenging benchmark and show that our method is able to

successfully link more than two fragments, which cannot be done by the other methods. We also demonstrate that DiffLinker can be conditioned on the target protein pocket; our model respects

geometric constraints imposed by the surrounding protein atoms and generates molecules that are structurally compatible with the corresponding pockets. To demonstrate the relevance of

DiffLinker in practical drug design applications, we provide three case studies where our method can be integrated into the fragment-based design of ligands to target heat shock protein 90

(Hsp90) and inosine 5′-monophosphate dehydrogenase (IMPDH), and scaffold hopping for improving selectivity for c-Jun N-terminal kinases (JNKs). To the best of our knowledge, DiffLinker is

the first method that is not limited by the number of input fragments and accounts the information about pockets. The overall goal of this work is to provide practitioners with an effective

tool for molecular linker generation in realistic drug design scenarios. RESULTS We evaluate our method on four benchmarks in several different scenarios. First, we report the performance of

DiffLinker on ZINC13 and CASF14 datasets that contain only pairs of fragments to be connected. Next, we introduce a new dataset based on GEOM molecules15, where each entry contains two or

more separate fragments. For all three sets we experiment with different modalities of our method: with predefined or sampled linker size and with known or unknown anchor points.

Additionally, we assess the ability of DiffLinker to design relevant linkers in the presence of the protein pocket. For that, we introduce another dataset based on Binding MOAD16. Besides

standard metrics used in the previous benchmarks, we measure the number of steric clashes between generated linkers and surrounding protein atoms. Finally, we demonstrate the applicability

of DiffLinker in fragment-based design of Hsp90 and IMPDH inhibitors and in scaffold hopping for improving selectivity for JNKs. More details on datasets, baselines and metrics can be found

in Methods. CONNECTING FRAGMENT PAIRS While DiffLinker shows greater flexibility and applicability in different scenarios than other methods, we show below that it also outperforms them on

standard benchmarks ZINC and CASF in terms of chemical relevance (namely, the quantitative estimate of drug-likeness (QED), synthetic accessibility (SA) and number of rings) of the generated

molecules. As shown in Table 1, molecules generated by DiffLinker are predicted to be more synthetically accessible and demonstrate higher drug-likeness, which is important for drug design

applications. Moreover, our molecules usually share higher chemical and geometric similarity with the reference molecules as demonstrated by the SCRDKit scores given in Supplementary Table

5. In terms of validity, our models perform on par with the other methods. Note that both DeLinker and 3DLinker are autoregressive approaches that explicitly employ valency rules at each

generation step, while our model is shown to learn these rules from the data. Remarkably, the validity of the reference molecules from CASF with covalent bonds computed by OpenBabel is 92.2%

while our model generated molecules with 90.2% validity. Notably, sampling the size of the linker substantially improves novelty and uniqueness of the generated linkers without serious

degradation of the most important metrics. In this experiment, we considered four different versions of DiffLinker depending on the amount of the prior information on anchors and linker

length available at the sampling stage. Overall, the information about anchors helps to achieve higher validity and novelty of the generated samples, and this modality is preferred if such

information is available. On the other hand, if anchor atoms are unknown, the resulting samples are more diverse as sampled linkers connect different pairs of atoms. Sampling linker length

increases the diversity and novelty of the designed molecules while other metrics such as drug-likeness, SA and validity slightly degrade. In many drug design applications, uniqueness plays

a crucial role, and chemical diversity provides chemists with more options to consider and test. In such cases, the DiffLinker model with minimum prior information (anchor atoms and linker

size are unknown) is preferred. Examples of linkers generated by DiffLinker for different input fragments are shown in Extended Data Fig. 1. CONNECTING MULTIPLE FRAGMENTS One of the major

advantages of DiffLinker compared to recently developed autoregressive models DeLinker and 3DLinker is one-shot generation of the linker between any arbitrary number of fragments. This

overcomes the limitation of DeLinker and 3DLinker, which can only link two fragments at a time. Although these autoregressive models can be adjusted to connect pairs of fragments iteratively

while growing the molecule, the full context cannot be taken into account in this case. Therefore, suboptimal solutions are more likely to be generated. To illustrate this difference, we

adapted DeLinker and 3DLinker to iteratively connect pairs of fragments in molecules where more than two fragments should be connected and tested all the methods on the GEOM dataset. As

shown in Table 1, 3DLinker fails to construct valid molecules in almost 84% of cases and cannot recover any reference molecule, as shown in Supplementary Table 5. Despite the higher

complexity of linkers in this dataset, our models achieve 93% validity and recover more than 85% of the reference molecules. DeLinker fails to generate valid molecules in almost 100% of

samples. Besides, molecules generated by 3DLinker have no rings in the linkers, have substantially lower QED and are predicted to be harder to synthesize. Examples of linkers generated by

DiffLinker for different input fragments are provided in Extended Data Fig. 2. An example of the DiffLinker sampling process for a molecule from the GEOM dataset is shown in Fig. 1b.

POCKET-CONDITIONED LINKER DESIGN To illustrate the ability of DiffLinker to leverage the structural information provided by the target’s pockets, we trained three models on the Pockets

dataset (Methods). These models were conditioned on the full-atom pocket representation, on the backbone atoms only and unconditioned, which serves as a baseline to evaluate the pocket

conditioning. We computed the standard metrics reported in Supplementary Tables 6 and 7, as well as the number of steric clashes between generated molecules and the pockets. Clashes between

two atoms are defined based on the distance between them and their van der Waals radii. As shown in Fig. 2b, the model conditioned on the full-atom pocket representation generates molecules

with similar levels of steric clashes to those of the reference complexes from the test set. There is a clear trend in the number of clashes depending on the level of resolution of the

pockets on which DiffLinker is conditioned, where conditioning on full-atom pockets generates molecules with less steric clashes. To highlight the benefits of a reduced search space when

using a fragment-based approach, we also compare the results of our full-atom conditioned model with two fully de novo generation methods. We choose ResGen17, a 3D autoregressive method, and

DiffSBDD18, a conceptually similar diffusion model, as our baselines and evaluate the predicted binding propensity. In particular, we use GNINA19 to relax the generated molecules in the

pocket and calculate an estimate of the binding affinity. As shown in Fig. 2c, DiffLinker produces molecules with lower predicted binding affinity and poses that agree better with the

orthogonal docking method GNINA than those generated without predefined fragments. CASE STUDIES Here we demonstrate how DiffLinker can be integrated in real-world pipelines for drug design

and discuss three scenarios taken from the literature: fragment-based design of Hsp90 and IMPDH inhibitors, and scaffold hopping for improving selectivity for JNKs. DESIGN OF HSP90

INHIBITORS Hsp90 is a molecular chaperone involved in enabling the folding of numerous proteins, including those participating in oncogenic transformations. The authors of ref. 20 proposed a

potent inhibitor for Hsp90 using fragment-based screening and structure-based design techniques. First, using biochemical screening followed by X-ray crystallography, ref. 20 identified

fragments bound to separate subsites within the ATPase pocket of Hsp90 (Protein Data Bank (PDB) code 3HZ1), as shown in Fig. 3a. The authors report that by linking these fragments, compounds

with more than 1,000-fold improvement in affinity over the initial fragment hit were generated. A crystal structure of the reported inhibitor bound to Hsp90 is shown in Fig. 3c. In our

experiment, we follow the overall procedure reported in ref. 20 and integrate DiffLinker in the fragment-linking step. We consider two experimentally observed fragments bound to the ATPase

pocket of Hsp90 (Fig. 3a), remove the methyl ester group from one of them (Fig. 3b) and generate 1,000 linkers using the pocket-conditioned model. To predict the size of the linker, we use a

graph neural network (GNN) trained on the ZINC dataset. We note that the inhibitor reported in ref. 20 was not included in the Pockets and ZINC training sets. Additionally, none of the

relevant crystal structures was included in the Pockets training set. DiffLinker successfully recovers the inhibitor reported in ref. 20. Among 1,000 samples, three have the same chemical

structure as the reference ligand. The molecule with the highest SCRDKit score, which captures the highest geometric and chemical similarity to the reference compound, is shown in Fig. 3d.

Additionally, we generated 1,000 linkers with the model trained on the ZINC dataset (without pocket conditioning). Having the reference molecule and samples generated by two different

DiffLinker models, we scored the protein-ligand complexes with GNINA19 and Vina21, as implemented in the GNINA package. We use GNINA and Vina as proxies for binding energy, as these methods

are fast, and their predictions present some level of correlation with experimentally determined binding affinities, as shown in Extended Data Fig. 3 and discussed in more detail in

Supplementary Information. As shown in Fig. 3e,f, docking scores of the molecules sampled by the model conditioned on the protein pocket are improved relative to those by DiffLinker trained

on the ZINC dataset only (_P_ values of a two-sided Kolmogorov–Smirnov test are 1.832 × 10−124 and 1.460 × 10−175 for GNINA and Vina scores, respectively). Notably, some of the sampled

molecules have docking scores superior to those of the best pose of the reference compound. We additionally note that docking scores of all three DiffLinker samples that reproduce the

reference inhibitor molecule are comparable with scores of the reference, as depicted by dashed and solid lines in Fig. 3e,f. DESIGN OF IMPDH INHIBITORS IMPDH is an attractive tuberculosis

drug target which plays an important role in de novo synthesis of guanine nucleotides. Using fragment-based screening and structure-based design techniques, ref. 6 identified potent IMPDH

inhibitors. Having started with two initial fragment hits shown in Fig. 4a (PDB code 5OU2), the authors reported three successful compounds obtained through fragment linking. These compounds

are represented in Fig. 4f. Notably, the authors achieved more than 1,000-fold improvement in affinity over the initial fragment hits with the most potent candidate, compound 31. The

crystal structure of the protein complexed with the compound is shown in Fig. 4c (PDB code 5OU3). We generated 1,000 linkers of length 5 and 6 using the pocket-conditioned model. DiffLinker

recovered compound 30 and compound 31, which are some of the most potent inhibitors among those reported in ref. 6. Sampled molecules that reproduce these compounds with the highest SCRDKit

score are shown in Fig. 4d,e. Even though DiffLinker did not reproduce compound 29, it generated similar molecules in terms of Tanimoto distance. In Fig. 4g, we provide the top three closest

samples with their Tanimoto distances. Finally, following our previous experiment with Hsp90 inhibitors, we compute GNINA docking scores for DiffLinker samples and represent them also

relative to the score of the reference crystallized compound 31 in Fig. 4h. Vina scores for the same molecules are provided in Extended Data Fig. 4a. We highlight the scores of eight samples

that reproduce compound 31. We note that all eight samples show similar docking scores to the reference crystal structure. To better understand the differences between the reference and

sampled molecules, we computed the interactions between the reference molecule and the IMPDH pocket residues using PLIP22. We also computed the interactions between the DiffLinker sample

that reproduces compound 31 with the highest docking score and the target pocket. As shown in Fig. 4h, the reference and sampled linkers interact differently with the pocket. While the

reference linker interacts with the pocket through the acceptor oxygen that forms a hydrogen bond with the nitrogen of Glu-318, the sampled linker interacts with the pocket through the

nitrogen donor that forms a hydrogen bond with the oxygen of Glu-318. This difference in the interactions and docking scores suggests that our model explores the space of possible ligand

conformations trying to find favourable interactions with the protein pocket. IMPROVING SELECTIVITY OF JNK INHIBITORS JNKs constitute an important protein family of mitogen-activated protein

kinases that regulate various cellular processes, including cell proliferation, apoptosis, autophagy and inflammation23. Kamenecka et al.24 designed JNK3-selective inhibitors that had more

than 1,000-fold selectivity over p38, another closely related mitogen-activated protein kinase family member. Starting with the indazole class of compounds and by changing the compound’s

scaffold, the authors obtained an aminopyrazole scaffold that resulted in compounds with over 2,800-fold JNK-selectivity. Crystal structures of compounds with indazole and aminopyrazole

scaffolds reported in ref. 24 are shown in Fig. 5a,b. Here, we study the ability of DiffLinker to generate a set of diverse scaffolds. We input the structure of fragments with the missing

core (taken from indazole crystal structure, PDB code 3FI3) and generate 1,000 scaffolds with 8 and 9 atoms using our pocket-conditioned model. DiffLinker recovered both indazole and

aminopyrazole scaffolds, as observed in the ground-truth compounds. Following the previous experiments, we provide docking scores of DiffLinker samples in Extended Data Fig. 4b,c. Sampled

molecules that reproduce compounds reported in ref. 24 with the highest SCRDKit score are shown in Fig. 5c,d respectively. Overlay of real (green) and sampled (orange) indazole and

aminopyrazole structures is shown in Fig. 5e,f. In addition, we identified 238 unique topologies of the generated scaffolds, which suggests that DiffLinker is able to extensively explore the

space of potentially relevant scaffolds through the sampling of linker regions. Six most common distinct topologies along with the exemplary DiffLinker samples are represented in Fig. 5g.

For each of the represented moieties, we also provide the number of unique sampled chemical structures employing this topology. While none of the relevant crystal structures was included in

the training set, we note that indazole and aminopyrazole moieties are among the most commonly sampled ones. DISCUSSION In this work, we introduced DiffLinker, a new E(3)-equivariant 3D

conditional diffusion model for molecular linker design. Our method showed several desirable and practical features that have the potential to help accelerate the development of prospective

drug candidates using FBDD strategies. However, several aspects remain for further improvement; for instance, chemical validity of the sampled compounds is a necessary requirement for a

successful molecule design method. As explained in Supplementary Information, lower validity of DiffLinker samples is caused by the fact that our model generates raw point clouds, which are

then processed by OpenBabel25 to compute covalent bonds. In contrast, other methods construct bonds and employ valency rules at each generation step explicitly. While our model clearly

demonstrates the ability to effectively learn fundamental chemistry from the raw geometric data, several options that could be beneficial remain to be tested. One possible direction is

incorporating the information on covalent bonds to the model (that is, adding edge features) and generating chemical bonds along with atom types and coordinates. Another important property

of the sampled molecules is high SA. This quality plays a crucial role in real-world drug discovery pipelines. In the current work, we report SA score26 and show that DiffLinker produces

more synthetically accessible molecules, compared to other linker design methods; however, there still remains room for improvement. While the current model gets a notion of SA only from the

raw training data, one may explicitly employ this concept in the method by guiding the denoising process with, for instance, SA score26. While DiffLinker effectively suggests diverse and

valid chemical structures in tasks like fragment linking and scaffold hopping, we have observed that generating relevant linkers for PROTAC-like molecules poses a greater challenge. The main

difference between these problems lies on the linker length and the distance between the input fragments. While the average linker size in our training sets is around 8 atoms (5 for ZINC,

10 for GEOM, 10 for Pockets), a typical linker in a PROTAC varies between 12 and 20 atoms27. It means that the distribution of linkers in PROTACs has different characteristics compared to

the distributions of linkers provided in our training sets. Therefore, to improve the performance of DiffLinker in PROTAC design, one may consider retraining the model using more suitable

PROTAC data. Finally, although the current work focuses on molecular linker design, DiffLinker can facilitate other stages of fragment-based drug discovery, as there are no fundamental

limitations in applying our model to molecule growing or de novo generation of molecular fragments. METHODS Here we describe DiffLinker, an E(3)-equivariant diffusion model for generating

molecular linkers conditioned on 3D fragments. First, we provide an overview of diffusion models and discuss the data representation and equivariance. Next, we formulate equivariance

requirements for the underlying denoising distributions and propose an appropriate learnable dynamic function. We also discuss the strategy of sampling the size of a linker and conditioning

on protein pockets. Finally, we provide information on datasets, evaluation methodology, baselines and sampling efficiency of DiffLinker. The full linker generation workflow is schematically

represented in Fig. 1, and the pseudocode of DiffLinker’s training and sampling procedures is provided in Supplementary Information. DIFFUSION MODELS Diffusion models28 are a class of

generative methods that consist of a ‘diffusion process’, which progressively transforms a data point X into noise and a ‘generative denoising model’, which approximates the reverse of the

diffusion process. In this paper, we consider Gaussian diffusion: at a time step _t_ = 0, …, _T_, the conditional distribution of the intermediate data state Z_t_ given previous state Z_t_−1

is defined by the multivariate normal distribution, $$q({{{{{\bf{z}}}}}}_{t}| {{{{{\bf{z}}}}}}_{t-1})={{{\mathcal{N}}}}({{{{{\bf{z}}}}}}_{t};\,{\overline{\alpha

}}_{t}{{{{{\bf{z}}}}}}_{t-1},\,{\overline{\sigma }}_{t}^{\,2}{{{{\textit{I}}}}}),$$ (1) where _I_ is an identity matrix, parameter \({\overline{\alpha }}_{t}\in {{\mathbb{R}}}^{+}\) controls

how much signal is retained and parameter \({\overline{\sigma }}_{t}\in {{\mathbb{R}}}^{+}\) controls how much noise is added. The noise model is chosen to be Markovian, such that the

probability of a trajectory can be written as: $$q({{{{{\bf{z}}}}}}_{0},{{{{{\bf{z}}}}}}_{1},\ldots ,{{{{{\bf{z}}}}}}_{T}| {{{{\bf{x}}}}})=q({{{{{\bf{z}}}}}}_{0}| {\bf{x}})\mathop{\prod

}\limits_{t=1}^{T}q({{{{{\bf{z}}}}}}_{t}| {{{{{\bf{z}}}}}}_{t-1}),$$ (2) where Z_T_ is the data state at time step _T_. As the distribution _q_ is normal, a simple formula for the

distribution of Z_t_ given X can be derived: $$q({{{{{\bf{z}}}}}}_{t}| {{{{\bf{x}}}}})={{{\mathcal{N}}}}({{{{{\bf{z}}}}}}_{t}| {\alpha }_{t}{{{{\bf{x}}}}},{\sigma

}_{t}^{2}{{{{\textit{I}}}}}),$$ (3) where \({\overline{\alpha }}_{t}={\alpha }_{t}/{\alpha }_{t-1}\) and \({\overline{\sigma }}_{t}^{\,2}={\sigma }_{t}^{2}-{\overline{\alpha

}}_{t}^{\,2}{\sigma }_{t-1}^{2}\). This closed-form expression shows that noise does not need to be added iteratively to X to achieve an intermediate state Z_t_. Another key property of

Gaussian noise is that the reverse process of the diffusion, referred to as the true denoising process, also admits a closed-form solution when conditioned on the original data point X:

$$q({{{{{\bf{z}}}}}}_{t-1}| {{{{\bf{x}}}}},{{{{{\bf{z}}}}}}_{t})={{{\mathcal{N}}}}({{{{{\bf{z}}}}}}_{t-1};{{{{\bf{\upmu}}}}}_{t}({{{{\bf{x}}}}},{{{{{\bf{z}}}}}}_{t}),{\varsigma

}_{t}^{2}{{{{\textit{I}}}}}),$$ (4) where distribution parameters Μ_t_ and ς_t_ can be derived analytically: $${{{{\bf{\upmu

}}}}}_{t}({{{{\bf{x}}}}},{{{{{\bf{z}}}}}}_{t})=\frac{{\overline{\alpha }}_{t}{\sigma }_{t-1}^{2}}{{\sigma }_{t}^{2}}{{{{{\bf{z}}}}}}_{t}+\frac{{\alpha }_{s}{\overline{\sigma

}}_{t}^{\,2}}{{\sigma }_{t}^{2}}{{{{\bf{x}}}}}\,\,{{{\rm{and}}}}\,\,{\varsigma }_{t}=\frac{{\overline{\sigma }}_{t}{\sigma }_{t-1}}{{\sigma }_{t}}.$$ (5) This formula describes that if a

diffusion trajectory starts at X and ends at Z_T_, then the expected value of any intermediate state is an interpolation between X and Z_T_. The second component of a diffusion model is the

generative denoising process, which aims to invert the diffusion trajectory by approximating the original data point X using a neural network. The generative transition distribution is then

defined as: $$p({{{{{\bf{z}}}}}}_{t-1}| {{{{{\bf{z}}}}}}_{t})=q({{{{{\bf{z}}}}}}_{t-1}| \hat{{{{{\bf{x}}}}}},{{{{{\bf{z}}}}}}_{t}),$$ (6) where \(\hat{\bf{x}}\) is an approximation of the

data point X computed by a neural network _φ_. Instead of predicting X directly, ref. 29 has empirically shown that it is more effective to first predict the Gaussian noise

\({\hat{{{{\bf{\upepsilon}}}}}}_{t}=\varphi ({{{{{\bf{z}}}}}}_{t},t)\) and then estimate \(\hat{{{{{\bf{x}}}}}}\) based on equation (3): $$\hat{{{{{\bf{x}}}}}}=(1/{\alpha

}_{t}){{{{{\bf{z}}}}}}_{t}-({\sigma }_{t}/{\alpha }_{t}){\hat{{{{\bf{\upepsilon }}}}}}_{t}.$$ (7) The neural network is trained to maximize an evidence lower bound on the likelihood of the

data under the model. Up to a prefactor that depends on _t_, this objective is equivalent to the mean squared error between predicted and true noise29,30. Therefore, we use the simplified

objective \({{{\mathcal{L}}}}(t)=| | {{{\bf{\upepsilon}}}}-{\hat{{{{\bf{\upepsilon}}}}}}_{t}| {|}^{2}\) that can be optimized by mini-batch gradient descent using an estimator

\({{\mathbb{E}}}_{t \sim {{{{{\bf{u}}}}}}(0,\ldots ,T)}[T{{{\mathcal{L}}}}(t)]\). Finally, once the network is trained, it can be used to sample new data points. For this purpose, one first

samples the Gaussian noise: \({{{{{\bf{z}}}}}}_{T} \sim {{{\mathcal{N}}}}(0,{{{{\textit{I}}}}})\). Then, for _t_ = _T_, …, 1, one should iteratively sample Z_t_−1 ~ _p_(Z_t_−1∣Z_t_) and

finally sample X ~ _p_(X∣Z0), where Z0 is the data state at the time step _t_ = 0. MOLECULE REPRESENTATION AND EQUIVARIANCE In our model, molecules are represented as 3D atomic point clouds.

A molecule is represented by the coordinates of its _M_ atoms \({{{{\bf{r}}}}}=({{{{{\bf{r}}}}}}_{1},\ldots ,{{{{{\bf{r}}}}}}_{M})\in {{\mathbb{R}}}^{M\times 3}\) and their corresponding

feature vectors, \({{{{\bf{h}}}}}=({{{{{\bf{h}}}}}}_{1},\ldots ,{{{{{\bf{h}}}}}}_{M})\in {{\mathbb{R}}}^{M\times {{{\rm{nf}}}}}\), which are one-hot encoded atom types. We refer to this

point cloud as X = [R, H]. While atomic coordinates are continuous, atom types are discrete variables that need to be handled differently in our diffusion model. Instead of using categorical

diffusion models31,32, we use a simpler strategy33 that lifts the atom types to a continuous space using one-hot encoding and adding Gaussian noise. The continuous values are then converted

back to discrete values through argmax over the different categories during the final transition from Z0 to X. For more details on the structure of the final transition distribution

_p_(X∣Z0) and likelihood computation, we refer the reader to ref. 33. To process 3D molecules efficiently, the data symmetries need to be respected. In this work, we consider the Euclidean

group E(3) that comprises translations, rotations and reflections of \({{\mathbb{R}}}^{3}\) and the orthogonal group O(3) that includes rotations and reflections of \({{\mathbb{R}}}^{3}\). A

function _f_ is E(3)-equivariant if for any point cloud X, orthogonal matrix \({{{{\textit{R}}}}}\in {{\mathbb{R}}}^{3\times 3}\) and translation vector \({{{{\bf{t}}}}}\in

{{\mathbb{R}}}^{3}\) we have: _f_(_R_X + T) = _R__f_(X) + T. Note that for simplicity, we use notation

\({{{{\textit{R}}}}}{{{{\bf{x}}}}}+{{{{\bf{t}}}}}=[{({{{{\textit{R}}}}}{{{{{\bf{r}}}}}}_{1}+{{{{\bf{t}}}}},\ldots ,{{{{\textit{R}}}}}{{{{{\bf{r}}}}}}_{M}+{{{{\bf{t}}}}})}^{\top

},{{{{\bf{h}}}}}]\). A conditional distribution _p_(X∣Y) is E(3)-equivariant if for any point clouds X, Y, _p_(_R_X + T∣_R_Y + T) = _p_(X∣Y). Finally, a function _f_ and a distribution _p_

are O(3)-equivariant if _f_(_R_X) = _R__f_(X) and _p_(_R_X∣_R_Y) = _p_(X∣Y), respectively. We call the function _f_ translation invariant if _f_(X + T) = _f_(X). EQUIVARIANT 3D CONDITIONAL

DIFFUSION MODEL Unlike other diffusion models for molecule generation33,34, our method is conditioned on three-dimensional data. More specifically, we assume that each point cloud X has a

corresponding ‘context’ U, which is another point cloud consisting of all input fragments and (optionally) protein pocket atoms that remain unchanged throughout the diffusion and denoising

processes, as shown in Fig. 1. Hence, we consider the generative process from equation (6) to operate on point cloud X while being conditioned on the fixed corresponding context:

$$p({{{{\bf{z}}}}}_{t-1}| {{{{{\bf{z}}}}}}_{t},{{{{\bf{u}}}}})=q({{{{{\bf{z}}}}}}_{t-1}| \hat{{{{{\bf{x}}}}}},{{{{{\bf{z}}}}}}_{t}),\,{{{\rm{where}}}}\,\hat{{{{{\bf{x}}}}}}=(1/{\alpha

}_{t}){{{{{\bf{z}}}}}}_{t}-({\sigma }_{t}/{\alpha }_{t})\varphi ({{{{{\bf{z}}}}}}_{t},{{{{\bf{u}}}}},t).$$ (8) The presence of a 3D context puts additional requirements on the generative

process, as it should be equivariant to its transformations. PROPOSITION 1 Consider a prior noise distribution \(p({{{{{\bf{z}}}}}}_{T}|

{{{{\bf{u}}}}})={{{\mathcal{N}}}}({{{{{\bf{z}}}}}}_{T};{{{\bf{\upmu }}}},{{{{\textit{I}}}}})\), where \({{{\bf{\upmu }}}}=[\,f({{{{{\bf{z}}}}}}_{T}),{{{\boldsymbol{0}}}}]\in

{{\mathbb{R}}}^{M\times (3+{{{\rm{nf}}}})}\), and \(f:{{\mathbb{R}}}^{M\times (3+{{{\rm{nf}}}})}\to {{\mathbb{R}}}^{M\times 3}\) is a function operating on 3D point clouds. Consider

transition distributions \(p({{{{{\bf{z}}}}}}_{t-1}| {{{{{\bf{z}}}}}}_{t},{{{{\bf{u}}}}})=q({{{{{\bf{z}}}}}}_{t-1}| \hat{{{{{\bf{x}}}}}},{{{{{\bf{z}}}}}}_{t})\), where _q_ is an isotropic

Gaussian and \(\hat{{{{{\bf{x}}}}}}\) is an approximation computed by the neural network _φ_ according to equation (8). Let the conditional denoising probabilistic model _p_ be a Markov

chain defined as $$p({{{{{\bf{z}}}}}}_{0},{{{{{\bf{z}}}}}}_{1},\ldots ,{{{{{\bf{z}}}}}}_{T}| {{{{\bf{u}}}}})=p({{{{{\bf{z}}}}}}_{T}| {{{{\bf{u}}}}})\mathop{\prod

}\limits_{t=1}^{T}p({{{{{\bf{z}}}}}}_{t-1}| {{{{{\bf{z}}}}}}_{t},{{{{\bf{u}}}}}).$$ (9) If _f_ is O(3)-equivariant and _φ_ is equivariant to joint O(3)-transformations of Z_t_ and U, then

_p_(Z0∣U) is O(3)-equivariant. The choice of the function _f_ highly depends on the problem being solved and the available priors. In our experiments, we consider two cases. First, following

ref. 9, we make use of the information about atoms that should be connected by the linker. We call these atoms ‘anchors’ and define _f_(U) as the anchors’ centre of mass. However, in a

real-world scenario, it is unlikely to be known which atoms should be the anchors. Here we define _f_(U) as the centre of mass of the whole context U. We should note that although function

_f_ computes a single point in 3D, it outputs its coordinate vector repeated _M_ times along the first dimension (because the noise is further sampled independently for each atom of the

point cloud). We note that the probabilistic model _p_ is not equivariant to translations, as shown in Supplementary Information. To overcome this issue, we construct the network _φ_ to be

translation invariant. Then, instead of sampling the initial coordinates noise from \({{{\mathcal{N}}}}(\,f({{{{\bf{u}}}}}),{{{{\textit{I}}}}})\) we centre the data at _f_(U) and sample from

\({{{\mathcal{N}}}}({{{\boldsymbol{0}}}},{{{{\textit{I}}}}})\). This makes the generative process independent of translations. DYNAMICS The learnable function _φ_ that models the dynamics

of the diffusion model takes as input a noisy version of the linker Z_t_ at time _t_ and the context U. These two parts are modelled as a single fully connected graph where nodes are

represented by coordinates R and feature vectors H that include atom types, time _t_ fragment flags and (optionally) anchor flags. The predicted noise \(\hat{{{{\bf{\upepsilon }}}}}\)

includes coordinate and feature components: \(\hat{{{{\bf{\upepsilon }}}}}=[{\hat{{{{\bf{\upepsilon }}}}}}^{\rm{r}},{\hat{{{{\bf{\upepsilon }}}}}}^{\rm{h}}]\). The neural network is built

upon the E(3)-equivariant GNN (EGNN)35. EGNN consists of the composition of equivariant graph convolutional layers (EGCL) R_l_+1, H_l_+1 = EGCL[R_l_, H_l_], which are defined as

$${{{{{\bf{m}}}}}}_{ij}={\phi }_{\rm{e}}({{{{{\bf{h}}}}}}_{i}^{l},{{{{{\bf{h}}}}}}_{j}^{l},{d}_{ij}^{\,2}),\,\,\,{{{{{\bf{h}}}}}}_{i}^{l+1}={\phi

}_{\rm{h}}\left({{{{{\bf{h}}}}}}_{i}^{l},\mathop{\sum}\limits_{j\ne i}{{{{{\bf{m}}}}}}_{ij}\right),\,\,\,{{{{{\bf{r}}}}}}_{i}^{l+1}={{{{{\bf{r}}}}}}_{i}^{l}+{\phi

}_{\rm{vel}}({{{{{\bf{r}}}}}}^{l},{{{{{\bf{h}}}}}}^{l},i),$$ (10) where \({d}_{ij}=\parallel {{{{{\bf{r}}}}}}_{i}^{l}-{{{{{\bf{r}}}}}}_{j}^{l}\parallel\) and _ϕ_e and _ϕ_h are learnable

functions parametrized by fully connected neural networks (see Supplementary Information for details). The latter update for the node coordinates is computed by the learnable function

_ϕ_vel. Note that our graph includes both a noisy linker Z_t_ and a fixed context U, and _φ_ is intended to predict the noise that should be subtracted from the coordinates and features of

Z_t_. Therefore, it is natural to keep the context coordinates unchanged when computing dynamics and to apply non-zero displacements only to the linker part at each EGCL step. Hence, we

model the linker node displacements as follows, $${\phi }_{\rm{vel}}({{{{{\bf{r}}}}}}^{l},{{{{{\bf{h}}}}}}^{l},i)=\mathop{\sum}\limits_{j\ne

i}\frac{{{{{{\bf{r}}}}}}_{i}^{l}-{{{{{\bf{r}}}}}}_{j}^{l}}{{d}_{ij}+1}{\phi }_{\rm{r}}({{{{{\bf{h}}}}}}_{i}^{l},{{{{{\bf{h}}}}}}_{j}^{l},{d}_{ij}^{\,2}),$$ (11) where _ϕ_r is a learnable

function parametrized by a fully connected neural network. Displacements for the context nodes are always set to 0. The equivariance of convolutional layers is achieved by construction. The

messages _ϕ_e and the node updates _ϕ_h depend only on scalar node features and distances between nodes that are E(3)-invariant. Coordinate updates _ϕ_vel additionally depend linearly on the

difference between coordinate vectors \({{{{{\bf{r}}}}}}_{i}^{l}\) and \({{{{{\bf{r}}}}}}_{j}^{l}\), which makes them E(3)-equivariant. After the sequence of EGCLs is applied, we have an

updated graph with new node coordinates \(\hat{{{{{\bf{r}}}}}}=[{{{{{\bf{u}}}}}}^{\rm{r}},{\hat{{{{{\bf{z}}}}}}}_{t}^{\rm{r}}]\) and new node features

\(\widehat{{{{{\bf{h}}}}}}=[{\hat{{{{{\bf{u}}}}}}}^{\rm{h}},{\hat{{{{{\bf{z}}}}}}}_{t}^{\rm{h}}\,]\). Since we are interested only in the linker-related part, we discard the coordinates and

features of context nodes and consider the tuple \([{\hat{{{{{\bf{z}}}}}}_{t}^{\rm{r}},{\hat{{{{{\bf{z}}}}}}}_{t}^{\rm{h}}]}\) to be the EGNN output. To make the function _φ_ invariant to

translations, we subtract the initial coordinates from the coordinate component of the EGNN output following ref. 33: $$\hat{{{{\bf{\upepsilon }}}}}=[{\hat{{{{\bf{\upepsilon

}}}}}}^{\rm{r}},{\hat{{{{\bf{\upepsilon }}}}}}^{\rm{h}}]=\varphi

({{{{{\bf{z}}}}}}_{t},{{{{\bf{u}}}}},t)={{{\rm{EGNN}}}}({{{{{\bf{z}}}}}}_{t},{{{{\bf{u}}}}},t)-[{{{{{\bf{z}}}}}}_{t}^{\rm{r}},{{{\boldsymbol{0}}}}].$$ (12) LINKER-SIZE PREDICTION To predict

the size of the missing linker between a set of fragments, we represent fragments as a fully connected graph with one-hot encoded atom types as node features and distances between nodes as

edge features. From this, a separately trained GNN (see Supplementary Information for details) produces probabilities for the linker size. Our assumption is that relative fragment positions

and orientations, along with atom types, contain all the information essential for predicting the most likely size of the prospective linker. When generating a linker, we first sample its

size with the predicted probabilities from the categorical distribution over the list of linker sizes seen in the training data, as shown in Fig. 1. PROTEIN POCKET CONDITIONING In real-world

FBDD applications, it often occurs that fragments are obtained by experimental screening followed by structural determination3 or selected and docked into a target protein pocket36. To

propose a drug candidate molecule, the fragments have to be linked. When generating the linker, one should take the surrounding pocket into account and construct a linker that is sterically

compatible with the protein pocket and, if possible, also contributes to a potent binding affinity. To add pocket conditioning to DiffLinker, we represent a protein pocket as an atomic point

cloud and consider it as a part of the context U. We also extend node features with an additional binary flag marking atoms that belong to the protein pocket. Finally, as the new context

point cloud contains much more atoms, we modify the joint representation of the data point Z_t_ and the context U that are passed to the neural network _φ_. Instead of considering fully

connected graphs, we assign edges between nodes based on a 4 Å distance cutoff, as it makes the resulting graphs less dense and counterbalances the increase in the number of nodes. DATASETS

ZINC We follow ref. 9 and consider a subset of 250,000 molecules randomly selected by Gómez-Bombarelli et al.37 from the ZINC database13. First, we generate 3D conformers using RDKit38 and

define a reference 3D structure for each molecule by selecting the lowest energy conformation. Then, these molecules are fragmented by enumerating all double cuts of acyclic single bonds

that are not within functional groups. The resulting splits are filtered by the number of atoms in the linker and fragments, SA26, ring aromaticity and pan-assay interference compounds

(PAINS)39 criteria. One molecule can therefore result in various combinations of two fragments with a linker between. The resulting dataset is randomly split into train (438,610 examples),

validation (400 examples) and test (400 examples) sets. Atom types considered for this dataset are: C, O, N, F, S, Cl, Br and I. CASF Another evaluation benchmark used by ref. 9 is taken

from the CASF-2016 dataset14. In contrast to ZINC, where molecule conformers were generated computationally, CASF includes experimentally verified 3D conformations. Following the same

preprocessing procedures as for the ZINC dataset, ref. 9 obtained an additional test set of 309 examples, which we use in our work. Atom types considered for this dataset are: C, O, N, F, S,

Cl, Br and I. GEOM ZINC and CASF datasets used in previous works only contain pairs of fragments. However, real-world applications often require connecting more than two fragments with one

or more linkers36. To address this case, we construct a new dataset based on GEOM molecules15, which we decompose into three or more fragments with one or two linkers connecting them. To

achieve such splits, we use RDKit implementations of two fragmentation techniques—a matched molecular pair analysis (MMPA) based algorithm40 and BRICS41—and combine results, removing

duplicates. Overall, we obtain 41,907 molecules and 285,140 fragmentations that are randomly split in train (282,602 examples), validation (1,250 examples) and test (1,288 examples) sets.

Atom types considered for this dataset are: C, O, N, F, S, Cl, Br, I and P. POCKETS DATASET To assess the ability of DiffLinker to generate valid linkers given additional information about

protein pockets, we use the protein-ligand dataset curated by Schneuing et al.18 from Binding MOAD16. To define pockets, we consider amino acids that have at least one atom closer than 6 Å

to any atom of the ligand. All atoms belonging to these residues constitute the pocket. We split molecules into fragments using RDKit’s implementation of an MMPA-based algorithm40. We

randomly split the resulting data into train (185,678 examples), validation (490 examples) and test (566 examples) sets, taking into account Enzyme Commission numbers of the proteins. Atom

types considered for this dataset are: C, O, N, F, S, Cl, Br, I and P. METRICS First, we report several chemical properties of the generated molecules that are especially important in drug

design applications: average QED42, average SA26 and average number of rings in the linker. Next, following ref. 9, we measure validity, uniqueness and novelty of the samples. We then

determine if the generated linkers are consistent with the 2D filters used to produce the ZINC training set. These filters are explained in detail in Supplementary Information. In addition,

we record the percentage of the original molecules that were recovered by the generation process. To compare the 3D shapes of the sampled and ground-truth molecules, we estimate the root

mean squared deviation (r.m.s.d.) between the generated and real linker coordinates in the cases where true molecules are recovered. We also compute the SCRDKit metric that evaluates the

geometric and chemical similarity between the ground-truth and generated molecules43,44. BASELINES We compare our method with DeLinker9 and 3DLinker11 on the ZINC test set and with DeLinker

on the CASF dataset. We adapted DeLinker and 3DLinker to connect more than two fragments (see Supplementary Information for details) and evaluate its performance on the GEOM dataset. To

obtain 3D conformations for the molecules generated by DeLinker, we applied a pretrained ConfVAE45 followed by a force field relaxation procedure MMFF46. For all methods, including ours, we

generate linkers with the ground-truth size unless explicitly noted otherwise. To obtain SMILES representations of atomic point clouds generated by our models, we utilize OpenBabel25 to

compute covalent bonds between atoms. We also use OpenBabel to rebuild covalent bonds for the molecules in test sets to correctly compute the recovery rate, r.m.s.d. and SCRDKit scores for

our models. In ZINC and CASF experiments, we sample 250 linkers for each input pair of fragments. For the GEOM dataset and in experiments with pocket conditioning, we sample 100 linkers for

each input set of fragments. In our experiments with protein pockets as additional context, we compare DiffLinker with two de novo generation methods, ResGen17 and DiffSBDD18. In both cases,

we obtained trained model weights from the publicly available repositories and sample molecules with the default settings as described in the online documentation. We sample 120 new

molecules for each target with a version of DiffSBDD that uses the full-atomic pocket context. ResGen produced 100 molecules per target on average (minimum 19, maximum 149). SAMPLING For all

the experiments discussed in the main text, we sampled with the same number of denoising steps _T_ = 500 as used in training. Sampling time for all the datasets is provided in Supplementary

Table 10. Although the time reported in Supplementary Table 10 is more than affordable for applying our method in practice, we explored the capability of DiffLinker to sample even faster

without performance loss. Following ref. 47, we conducted an additional evaluation of DiffLinker with the reduced number of denoising steps _T_ = 500 in sampling, considering _T_/2, _T_/5,

_T_/10, _T_/20, _T_/50 and _T_/100 values. Extended Data Fig. 5 shows how the performance metrics obtained on the ZINC test set depend on the number of denoising steps performed in sampling.

In all cases, we used DiffLinker pretrained on ZINC with _T_ = 500 denoising steps. As shown in Extended Data Fig. 5, our model is robust to a notable reduction of the number of denoising

steps in sampling resulting in 10-fold gain in sampling speed without any performance degradation. Effectively, one can reduce the sampling speed from 0.365 to 0.036 seconds per molecule

with no substantial performance metrics loss. SOFTWARE Dataset processing was done in Python (v.3.10.5) using RDKit (v.2022.03.2) for generating molecular conformers and splitting them in

fragments and linkers, scikit-learn (v.1.0.1) for splitting datasets and BioPython (v.1.79) for processing protein structures. The MMPA-based algorithm40 and BRICS41 used for molecule

fragmentation, as well as force field relaxation procedure MMFF46, are components of The RDKit package. Central packages used for writing DiffLinker as well as training and sampling scripts

include NumPy (v.1.22.3), PyTorch (v.1.11.0), PyTorch Lightning (v.1.6.3), WandB (v.0.12.16), RDKit (v.2022.03.2) and OpenBabel (v.3.0.0). For sampling molecules with baseline methods, we

used pretrained models and sampling scripts available at the corresponding repositories: 3DLinker (https://github.com/YinanHuang/3DLinker)48, DeLinker (https://github.com/oxpig/DeLinker)49,

DiffSBDD (https://github.com/arneschneuing/DiffSBDD)50 and ResGen (https://github.com/HaotianZhangAI4Science/ResGen)51. None of these repositories provide version releases. Data analysis and

vizualization was done in Python (v.3.10.5) using RDKit (v.2022.03.2), imageio (v.2.19.2), NetworkX (v.2.8.4), SciPy (v.1.7.3), matplotlib (v.3.5.2), seaborn (v.0.11.2) and GNINA (v.1.0.3,

https://github.com/gnina/gnina)52. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY

All the processed datasets, as well as pretrained models, are available at Zenodo. Datasets: ZINC (https://doi.org/10.5281/zenodo.7121271)53, CASF (https://doi.org/10.5281/zenodo.7121264)54,

GEOM (https://doi.org/10.5281/zenodo.7121278)55, Pockets (https://doi.org/10.5281/zenodo.7121280)56. Models: https://doi.org/10.5281/zenodo.7775568 (ref. 57). Molecules used in the ZINC

dataset are available at the ZINC database (https://zinc.docking.org/). Molecules used in the CASF dataset were taken from the CASF-2016 benchmark package

(http://www.pdbbind.org.cn/download/CASF-2016.tar.gz) of the PDBbind database (http://www.pdbbind.org.cn/). Molecules used in the GEOM dataset are available at the repository of the original

GEOM dataset (https://github.com/learningmatter-mit/geom)58. Molecules used in the Pockets dataset were taken from Binding MOAD (http://www.bindingmoad.org/). Crystal structures of the

Hsp90 inhibitor and initially bound fragments are available at Protein Data Bank under the access codes 3HZ5 and 3HZ1, respectively. Crystal structures of the initial fragment hits and the

reported inhibitor for IMPDH are available at Protein Data Bank under the access codes 5OU2 and 5OU3, respectively. Crystal structures of JNK inhibitors with indazole and minopyrazole

scaffolds are available at Protein Data Bank under the access codes 3FI3 and 3FI2, respectively. CODE AVAILABILITY The source code of this study is freely available at GitHub

(https://github.com/igashov/DiffLinker)59,60. REFERENCES * Virshup, A. M., Contreras-García, J., Wipf, P., Yang, W. & Beratan, D. N. Stochastic voyages into uncharted chemical space

produce a representative library of all possible drug-like compounds. _J. Am. Chem. Soc._ 135, 7296–7303 (2013). Article  Google Scholar  * Erlanson, D. A., Fesik, S. W., Hubbard, R. E.,

Jahnke, W. & Jhoti, H. Twenty years on: the impact of fragments on drug discovery. _Nat. Rev. Drug Discov._ 15, 605–619 (2016). Article  Google Scholar  * Bancet, A. et al. Fragment

linking strategies for structure-based drug design. _J. Med. Chem._ 63, 11420–11435 (2020). Article  Google Scholar  * Sun, H., Tawa, G. & Wallqvist, A. Classification of

scaffold-hopping approaches. _Drug Discovery Today_ 17, 310–324 (2012). Article  Google Scholar  * Bai, N. et al. Rationalizing PROTAC-mediated ternary complex formation using Rosetta. _J.

Chem. Inf. Model._ 61, 1368–1382 (2021). Article  Google Scholar  * Trapero, A. et al. Fragment-based approach to targeting inosine-5′-monophosphate dehydrogenase (IMPDH) from Mycobacterium

tuberculosis. _J. Med.Chem._ 61, 2806–2822 (2018). Article  Google Scholar  * Sheng, C. & Zhang, W. Fragment informatics and computational fragment-based drug design: an overview and

update. _Med. Res. Rev._ 33, 554–598 (2013). Article  Google Scholar  * Yang, Y. et al. Syntalinker: automatic fragment linking with deep conditional transformer neural networks. _Chem.

Sci._ 11, 8312–8322 (2020). Article  Google Scholar  * Imrie, F., Bradley, A. R., Schaar, M. & Deane, C. M. Deep generative models for 3D linker design. _J. Chem. Inf. Model._ 60,

1983–1995 (2020). Article  Google Scholar  * Imrie, F., Hadfield, T. E., Bradley, A. R. & Deane, C. M. Deep generative design with 3D pharmacophoric constraints. _Chem. Sci._ 12,

14577–14589 (2021). Article  Google Scholar  * Huang, Y., Peng, X., Ma, J. & Zhang, M. 3DLinker: an E(3) equivariant variational autoencoder for molecular linker design. In _Proc. 39th

International Conference on Machine Learning_ (eds Chaudhuri, K. et al.) 9280–9294 (PMLR, 2022). * Weininger, D. SMILES, a chemical language and information system. 1. Introduction to

methodology and encoding rules. _J. Chem. Inf. Comput. Sci._ 28, 31–36 (1988). Article  Google Scholar  * Irwin, J. J. & Shoichet, B. K. ZINC – a free database of commercially available

compounds for virtual screening. _J. Chem. Inf. Model._ 45, 177–182 (2005). Article  Google Scholar  * Su, M. et al. Comparative assessment of scoring functions: the CASF-2016 update. _J.

Chem. Inf. Model._ 59, 895–913 (2018). Article  Google Scholar  * Axelrod, S. & Gómez-Bombarelli, R. GEOM, energy-annotated molecular conformations for property prediction and molecular

generation. _Sci. Data_ 9, 185 (2022). Article  Google Scholar  * Hu, L., Benson, M. L., Smith, R. D., Lerner, M. G. & Carlson, H. A. Binding MOAD (mother of all databases). _Proteins_

60, 333–340 (2005). Article  Google Scholar  * Zhang, O. et al. ResGen is a pocket-aware 3D molecular generation model based on parallel multiscale modelling. _Nat. Mach. Intell._ 5,

1020–1030 (2023). * Schneuing, A. et al. Structure-based drug design with equivariant diffusion models. Preprint at https://arxiv.org/abs/2210.13695 (2022). * McNutt, A. T. et al. GNINA 1.0:

molecular docking with deep learning. _J. Cheminform._ 13, 43 (2021). Article  Google Scholar  * Barker, J. J. et al. Discovery of a novel Hsp90 inhibitor by fragment linking. _ChemMedChem_

5, 1697–1700 (2010). Article  Google Scholar  * Trott, O. & Olson, A. J. AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization,

and multithreading. _J.Comput. Chem._ 31, 455–461 (2010). Article  Google Scholar  * Salentin, S., Schreiber, S., Haupt, V. J., Adasme, M. F. & Schroeder, M. PLIP: fully automated

protein–ligand interaction profiler. _Nucleic Acids Res._ 43, 443–447 (2015). Article  Google Scholar  * Chen, J. et al. The roles of c-Jun N-terminal kinase (JNK) in infectious diseases.

_Int. J. Mol. Sci._ 22, 9640 (2021). Article  Google Scholar  * Kamenecka, T. et al. Structure–activity relationships and X-ray structures describing the selectivity of aminopyrazole

inhibitors for c-Jun N-terminal kinase 3 (JNK3) over p38. _J. Biol. Chem._ 284, 12853–12861 (2009). Article  Google Scholar  * O’Boyle, N. M. et al. Open Babel: an open chemical toolbox. _J.

Cheminform._ 3, 33 (2011). Article  Google Scholar  * Ertl, P. & Schuffenhauer, A. Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and

fragment contributions. _J. Cheminform._ 1, 8 (2009). Article  Google Scholar  * Cyrus, K. et al. Impact of linker length on the activity of PROTACs. _Mol. Biosyst._ 7, 359–364 (2011).

Article  Google Scholar  * Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N. & Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In _Proc. 32nd International

Conference on Machine Learning_ (eds Bach, F. & Blei, D.) 2256–2265 (PMLR, 2015). * Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. In _Advances in Neural

Information Processing Systems 33_ (eds Larochelle, H. et al.) 6840–6851 (Curran Associates, 2020). * Kingma, D., Salimans, T., Poole, B. & Ho, J. Variational diffusion models. In

_Advances in Neural Information Processing Systems 34_ (eds Ranzato, M. et al.) 21696–21707 (Curran Associates, 2021). * Hoogeboom, E., Nielsen, D., Jaini, P., Forré, P. & Welling, M.

Argmax flows and multinomial diffusion: learning categorical distributions. In _Advances in Neural Information Processing Systems 34_ (eds Ranzato, M. et al.) 12454–12465 (Curran Associates,

2021). * Austin, J., Johnson, D. D., Ho, J., Tarlow, D. & Berg, R. Structured denoising diffusion models in discrete state-spaces. In _Advances in Neural Information Processing Systems

34_ (eds Ranzato, M. et al.) 17981–17993 (Curran Associates, 2021). * Hoogeboom, E., Satorras, V. G., Vignac, C. & Welling, M. Equivariant diffusion for molecule generation in 3D. In

_Proc. 39th International Conference on Machine Learning_ (eds Chaudhuri, K. et al.) 8867–8887 (PMLR, 2022). * Xu, M. et al. GeoDiff: a geometric diffusion model for molecular conformation

generation. In _International Conference on Learning Representations_ (OpenReview.net, 2022); https://openreview.net/forum?id=PzcvxEMzvQC * Satorras, V. G., Hoogeboom, E., Fuchs, F. B.,

Posner, I. & Welling, M. E(n) equivariant normalizing flows. In _Advances in Neural Information Processing Systems 34_ (eds Ranzato, M. et al.) 4181–4192 (Curran Associates, 2021). *

Igashov, I. et al. Decoding surface fingerprints for protein-ligand interactions. Preprint at _bioRxiv_ https://doi.org/10.1101/2022.04.26.489341 (2022). * Gómez-Bombarelli, R. et al.

Automatic chemical design using a data-driven continuous representation of molecules. _ACS Cent. Sci._ 4, 268–276 (2018). Article  Google Scholar  * RDKit: open-source cheminformatics

software. _RDKit_ https://rdkit.org (2013). * Baell, J. B. & Holloway, G. A. New substructure filters for removal of pan assay interference compounds (PAINS) from screening libraries and

for their exclusion in bioassays. _J. Med. Chem._ 53, 2719–2740 (2010). Article  Google Scholar  * Dossetter, A. G., Griffen, E. J. & Leach, A. G. Matched molecular pair analysis in

drug discovery. _Drug Discov. Today_ 18, 724–731 (2013). Article  Google Scholar  * Degen, J., Wegscheid-Gerlach, C., Zaliani, A. & Rarey, M. On the art of compiling and using

’drug-like’ chemical fragment spaces. _ChemMedChem_ 3, 1503–1507 (2008). Article  Google Scholar  * Bickerton, G. R., Paolini, G. V., Besnard, J., Muresan, S. & Hopkins, A. L.

Quantifying the chemical beauty of drugs. _Nat. Chem._ 4, 90–98 (2012). Article  Google Scholar  * Putta, S., Landrum, G. A. & Penzotti, J. E. Conformation mining: an algorithm for

finding biologically relevant conformations. _J. Med.Chem._ 48, 3313–3318 (2005). Article  Google Scholar  * Landrum, G. A., Penzotti, J. E. & Putta, S. Feature-map vectors: a new class

of informative descriptors for computational drug discovery. _J.Comput. Aided Mol. Des._ 20, 751–762 (2006). Article  Google Scholar  * Xu, M., Luo, S., Bengio, Y., Peng, J. & Tang, J.

Learning neural generative dynamics for molecular conformation generation. In _International Conference on Learning Representations_ (OpenReview.net, 2021);

https://openreview.net/forum?id=pAbm1qfheGk * Halgren, T. A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. _J. Comput. Chem._ 17, 490–519

(1996). Article  Google Scholar  * Nichol, A. Q. & Dhariwal, P. Improved denoising diffusion probabilistic models. In _Proc. 38th International Conference on Machine Learning_ (eds

Meila, M. & Zhang, T.) 8162–8171 (PMLR, 2021). * Huang, Y. 3DLinker. _GitHub_ https://github.com/YinanHuang/3DLinker (2022). * Oxford Protein Informatics Group. DeLinker. _GitHub_

https://github.com/oxpig/DeLinker (2019). * Schneuing, A. DiffSBDD. _GitHub_ https://github.com/arneschneuing/DiffSBDD (2022). * Zhang, O. ResGen. _GitHub_

https://github.com/HaotianZhangAI4Science/ResGen (2022). * McNutt, A. et al. gnina. _GitHub_ https://github.com/gnina/gnina (2021). * Igashov, I. et al. DiffLinker ZINC Dataset. _Zenodo_

https://doi.org/10.5281/zenodo.7121271 (2022). * Igashov, I. et al. DiffLinker CASF Dataset. _Zenodo_ https://doi.org/10.5281/zenodo.7121264 (2022). * Igashov, I. et al. DiffLinker GEOM

Dataset. _Zenodo_ https://doi.org/10.5281/zenodo.7121278 (2022). * Igashov, I. et al. DiffLinker Pockets Dataset. _Zenodo_ https://doi.org/10.5281/zenodo.7121280 (2022). * Igashov, I. et al.

DiffLinker Models. _Zenodo_ https://doi.org/10.5281/zenodo.7775568 (2022). * Axelrod, S. & Gomez-Bombarelli, R. learningmatter-mit/geom. _GitHub_

https://github.com/learningmatter-mit/geom (2022) * Igashov, I. et al. DiffLinker v.1.0. _GitHub_ https://github.com/igashov/DiffLinker (2024). * Igashov, I. & Stärk, H. DiffLinker: v1.0

_Zenodo_ https://doi.org/10.5281/zenodo.10515727 (2024). Download references ACKNOWLEDGEMENTS We thank Y. Du, J. Southern and V. Oleinikovas for helpful feedback and insightful discussions.

I.I. has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 945363. C.V. thanks the Swiss Data

Science Center for supporting him through the PhD fellowship programme (grant P18-11). M.B. is partially funded by the EPSRC Turing AI World-Leading Research Fellowship (grant EP/X040062/1).

FUNDING Open access funding provided by EPFL Lausanne. AUTHOR INFORMATION Author notes * Max Welling Present address: University of Amsterdam, Amsterdam, The Netherlands AUTHORS AND

AFFILIATIONS * École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland Ilia Igashov, Clément Vignac, Arne Schneuing, Pascal Frossard & Bruno Correia * Massachusetts Institute of

Technology, Cambridge, MA, USA Hannes Stärk * Microsoft Research AI4Science, Amsterdam, The Netherlands Victor Garcia Satorras & Max Welling * University of Oxford, Oxford, UK Michael

Bronstein Authors * Ilia Igashov View author publications You can also search for this author inPubMed Google Scholar * Hannes Stärk View author publications You can also search for this

author inPubMed Google Scholar * Clément Vignac View author publications You can also search for this author inPubMed Google Scholar * Arne Schneuing View author publications You can also

search for this author inPubMed Google Scholar * Victor Garcia Satorras View author publications You can also search for this author inPubMed Google Scholar * Pascal Frossard View author

publications You can also search for this author inPubMed Google Scholar * Max Welling View author publications You can also search for this author inPubMed Google Scholar * Michael

Bronstein View author publications You can also search for this author inPubMed Google Scholar * Bruno Correia View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS I.I. contributed to the main idea, conceptualization, code and manuscript writing. H.S. contributed to the main idea, code reorganization and docking experiments. C.V.

contributed to the mathematical conceptualization of the 3D conditional diffusion model and manuscript writing. A.S. contributed to the experiments with the methods for de novo molecule

generation and manuscript writing. V.G.S. and M.W. contributed to instruction and providing essential expertise in Euclidean diffusion models. P.F. and M.B. contributed to manuscript

revision and financial support. B.C. contributed to the main idea, experimental design, manuscript revision and funding acquisition. CORRESPONDING AUTHOR Correspondence to Bruno Correia.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Machine Intelligence_ thanks Jihan Kim and Tiago Rodrigues for

their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and

institutional affiliations. EXTENDED DATA EXTENDED DATA FIG. 1 EXAMPLES OF DIFFLINKER SAMPLES ON ZINC AND CASF DATASETS. Examples of linkers generated by DiffLinker (sampled size) for

fragments from CASF and ZINC datasets. EXTENDED DATA FIG. 2 EXAMPLES OF DIFFLINKER SAMPLES ON GEOM DATASET. Examples of linkers generated by DiffLinker (sampled size) for fragments from GEOM

datasets. EXTENDED DATA FIG. 3 CORRELATION OF GNINA SCORES AND EXPERIMENTALLY DETERMINED BINDING AFFINITIES. Predicted GNINA (A) and Vina (B) scores versus experimental KD values for Hsp90

proteins and their ligands (_n_ = 76) found in PDBbind database. Error bands show 95% confidence intervals using 1000 bootstrap samples. EXTENDED DATA FIG. 4 DISTRIBUTIONS OF DOCKING SCORES

FOR DIFFLINKER SAMPLES FOR IMPDH AND JNK. Distributions of Vina and GNINA scores for samples generated by DiffLinker. A, Vina scores of unique samples (_n_ = 800) for IMPDH. Red solid line

depicts the score of an experimentally validated compound 31 and blue dashed lines represent scores for eight DiffLinker samples that recover compound 31. B-C, Distributions of GNINA and

Vina scores correspondingly of unique samples (_n_ = 755) for JNK. Blue and red solid lines depict scores of experimentally validated compounds with indazole and aminopyrazole scaffolds.

Dashed magenta lines represent scores of eleven DiffLinker samples that recover compound with the indazole scaffold. EXTENDED DATA FIG. 5 DEPENDENCY OF DIFFLINKER PERFORMANCE ON THE NUMBER

OF SAMPLING STEPS. Dependency of validity, recovery and RMSD on the number of denoising steps in sampling shows that DiffLinker is robust to reducing the number of denoising steps. The

robustness of DiffLinker allows for 10-fold gain in sampling speed without any performance degradation. For all experiments we used DiffLinker trained on ZINC with 500 steps and performed

evaluation on ZINC test set sampling 250 linkers for each input set of fragments. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Sections 1–5, Figs. 1–3 and Tables 1–10.

REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation,

distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and

indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to

the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will

need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE

CITE THIS ARTICLE Igashov, I., Stärk, H., Vignac, C. _et al._ Equivariant 3D-conditional diffusion model for molecular linker design. _Nat Mach Intell_ 6, 417–427 (2024).

https://doi.org/10.1038/s42256-024-00815-9 Download citation * Received: 31 May 2023 * Accepted: 27 February 2024 * Published: 11 April 2024 * Issue Date: April 2024 * DOI:

https://doi.org/10.1038/s42256-024-00815-9 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative