News Reader.info

ABSTRACT Targeted hyperthermia treatment using magnetic nanoparticles is a promising cancer therapy. However, the mechanisms of heat dissipation in the large alternating magnetic field used

during such treatment have not been clarified. In this study, we numerically compared the magnetic loss in rotatable nanoparticles in aqueous media with that of non-rotatable nanoparticles

anchored to localised structures. In the former, the relaxation loss in superparamagnetic nanoparticles has a secondary maximum because of slow rotation of the magnetic easy axis of each

nanoparticle in the large field in addition to the known primary maximum caused by rapid Néel relaxation. Irradiation of rotatable ferromagnetic nanoparticles with a high-frequency axial

field generates structures oriented in a longitudinal or planar direction irrespective of the free energy. Consequently, these dissipative structures significantly affect the conditions for

maximum hysteresis loss. These findings shed new light on the design of targeted magnetic hyperthermia treatments. SIMILAR CONTENT BEING VIEWED BY OTHERS MAGNETIC NANOPARTICLES HYPERTHERMIA

IN A NON-ADIABATIC AND RADIATING PROCESS Article Open access 04 June 2021 HIGHLY EFFICIENT HEAT-DISSIPATION POWER DRIVEN BY FERROMAGNETIC RESONANCE IN _M_FE2O4 (_M_ = FE, MN, NI) FERRITE

NANOPARTICLES Article Open access 28 March 2022 ULTRA-HIGH RATE OF TEMPERATURE INCREMENT FROM SUPERPARAMAGNETIC NANOPARTICLES FOR HIGHLY EFFICIENT HYPERTHERMIA Article Open access 02 March

2021 INTRODUCTION Tumour-targeted magnetic hyperthermia has recently attracted much attention1. Preferential accumulation of magnetic nanoparticles in tumour tissue is achieved by

conjugating nanoparticles with tumour-homing peptides2 or antibodies3. When the accumulated nanoparticles are exposed to a large alternating magnetic field, _H_ = _H_acsin(2π_f_·_t_), where

_H_ac is the amplitude of the field, _f_ is the frequency and _t_ is time, they begin to rotate because of magnetic torque. Simultaneously, the direction of the magnetic moment, μ , in each

nanoparticle reverses with a certain probability. Consequently, heat equivalent to the magnetic loss dissipates locally in the tumour tissue. If the properties of the irradiated field are

limited (_i.e_., _H_ac·_f_ < constant)1 to ensure biomedical safety, then nanoparticles that maximise the _in vivo_ efficiency of heat dissipation, _P_H/(_H_ac·_f_), are required, where

_P_H is the specific energy dissipation rate (specific loss power) per unit mass of nanoparticles. The actual rotations of the nanoparticles are disordered because the microviscosity of the

local environment in cancer cells is not constant4,5 and effective elasticity depends on the binding conditions between nanoparticles and membranes. To minimise the effect of irregular

rotations in magnetic hyperthermia, two guiding principles have been proposed on the basis of simple models that consider a linear response of thermodynamic equilibrium states or magnetic

field-driven reversals. The first guiding principle6 is to use the relaxation loss in superparamagnetic iron oxide nanoparticles (SPIONs) with a sufficiently low energy barrier Δ_U_ for

reversal. If a linear response of their thermodynamic equilibrium state is considered at low _H_ac, the out-of-phase component of AC susceptibility χ″ can be expressed as follows: where χ 0

is the initial susceptibility per unit mass of SPIONs. When reversal and rotation occur in a nanoparticle in parallel, the characteristic time τ is given by the following equation: where τ N

is the Néel relaxation time for reversal and τ B is the Brownian relaxation time for rotation. Consequently, the heating efficiency _P_H/(_H_ac·_f _) = πμ0 χ″·_H_ac for individual

monodisperse nanoparticles has a single maximum at the peak frequency 2π_f_p = τ −1. For a sufficiently small SPION, τ is determined only by τ N because τ N is much shorter than τ B. In this

case, it has been assumed that the conditions for maximising the efficiency are unaffected by uncontrolled rotation of the nanoparticles. However, in some experiments, dual peaks have been

observed for the frequency dependence of χ″ ∝ _P_H/(_H_ac·_f _)7,8 despite the prediction of a single peak at a 2π_f_p value of τ −1 ( = τ N−1 + τ B−1). For this reason, size distribution7

or aggregation8 of the nanoparticles was considered based on the linear response theory. In an earlier study7, the low-frequency peak observed for the susceptibility was attributed to

Brownian relaxation of larger nanoparticles, while the high-frequency peak was attributed to Néel relaxation of smaller nanoparticles. In another study8, the low- and high-frequency peaks

were attributed to individual and agglomerated nanoparticles, respectively. Thus the observed dual peaks have been theoretically explained by the coexistence of two kinds of nanoparticles.

In other words, these explanations are based on the assumption that a single kind of nanoparticle will produce only a single peak at τ −1 ( = τ N−1 + τ B−1). However, this assumption has

never been theoretically verified under a large AC magnetic field, where the linear response theory does not hold. The second guiding principle is to use hysteresis loss in ferromagnetic

nanoparticles9. In mechanical models such as the Stoner–Wohlfarth model for single domain particles, μ is reversed in the time scale of Larmor precession (picoseconds) when Δ_U_ disappears

at the switching field _H_sw, because thermal fluctuations are not considered. Such fast reversals are considered to dominate the response to high frequency AC magnetic field because the

Brownian relaxations of large ferromagnetic nanoparticles are generally slow compared with the oscillation of the field. In this case, the work done in one cycle is given by the area inside

the hysteresis loop, ζ·_M_s·_H_sw, where _M_s is the spontaneous magnetisation and ζ is a coefficient related to the rectangularity of the loop. In the simple case of rectangular hysteresis

loops, ζ is 0 for _H_ac < _H_sw and 4 for _H_ac ≥ _H_sw. Consequently, the maximum efficiency, _P_H/(_H_ac·_f _) = ζ·_M_s·(_H_sw/_H_ac)/ρ, where ρ is the density of magnetite, is achieved

when _H_ac is adjusted to _H_sw. Because _H_sw depends on the magnetic anisotropy field _H_K specific to each nanoparticle, it has been assumed that, in cases where reversal is much faster

than rotation, the amount of hysteresis loss is unaffected by the inhomogeneous rotations of nanoparticles in cancer cells. In recent experimental studies10,11, the observed _P_H of

immobilised ferromagnetic nanoparticles was lower than that of the same nanoparticles dispersed in a fluid. Kim _et al_.10 attributed the difference to variation in the rates of convective

heat transfer. Müller _et al_.11 suggested that the orientation or agglomeration of the nanoparticles, or interaction effects, may be responsible for the observed difference. The orientation

of nanoparticles is important because it is related to the magnetic torque intrinsic in rotatable ferromagnetic nanoparticles. However, there has been no theoretical study on magnetic

field-driven reversals of μ in ferromagnetic nanoparticles with easy axes that simultaneously rotate under the magnetic torque. There are many reported inconsistencies between experimental

results and predictions based on the above two guiding principles for optimising hyperthermia treatment. These guiding principles are based on the simple models established at the two

limits: in zero magnetic field or at zero temperature. Under the conditions for hyperthermia (_H_ac ≠ 0, _T_ ≠ 0), where _T_ is temperature, the validity of the guiding principles has not

been theoretically verified even for an ideal system of non-interacting monodisperse nanoparticles. Consequently, we attempted to simulate the thermally assisted magnetic response of

individual superparamagnetic/ferromagnetic iron oxide nanoparticles exposed to a large AC magnetic field like that used in hyperthermia treatment. The simulation was performed in the

following two extreme cases: non-rotatable nanoparticles strongly anchored to structures resembling organelles and rotatable nanoparticles in an aqueous phase mimicking cytoplasm. In the

simulations, the thermally activated reversals of μ were calculated between the meta-stable directions. Simultaneously, the rotations of the spheroidal nanoparticles were computed in the

inertialess limit (Brownian dynamics simulation), where the frictional torque always balances with magnetic torque and with Brownian torque (details are reported in the Methods section). The

results allow examination of whether the relaxation loss for τ N « τ B and the hysteresis loss at _H_ac ≈ _H_sw are independent of the ability of the nanoparticles to rotate under the

conditions for hyperthermia treatment. RESULTS The magnetic response to an AC magnetic field _H_acsin(2π_f_·_t_) at T = 310 K was simulated for individual monodisperse spheroidal magnetite

nanoparticles with non-magnetic surfactant layers in non-rotatable and rotatable situations (see the Methods section for details). Results are presented for the following representative

nanoparticles: nearly spherical nanoparticles with an aspect ratio, κ , of 1.1 and an equatorial diameter, 2_R_M, of 18 nm and elongated spheroidal particles with κ = 1.4 and 2_R_M = 24 nm.

The parameters of these nanoparticles are summarised in Table 1. The former nanoparticles with τ N (_H_ac = 0) of 20 ns can be considered as typical SPIONs, while the latter with τ N (_H_ac

= 0) of 2×107 s (1 year) can be regarded as typical ferromagnetic nanoparticles in the frequency range of hyperthermia treatment ((2π_f _)−1 of approximately 1 μs). Results for nanoparticles

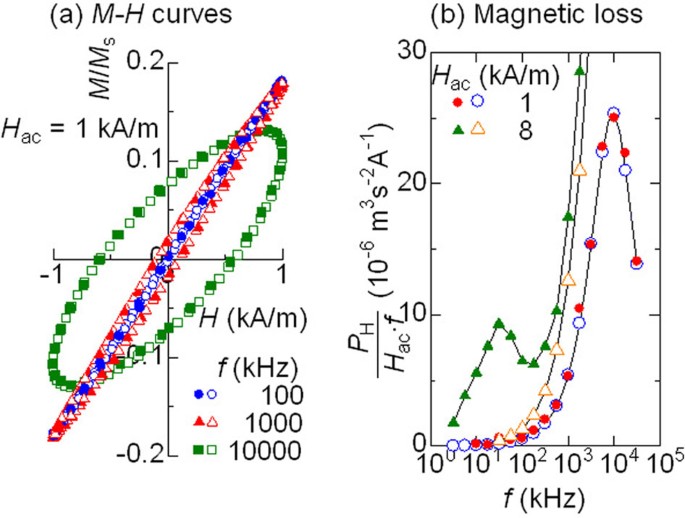
with other sizes and shapes are shown in the Supplementary Information. The magnetisation curves of the non-rotatable nearly spherical nanoparticles at low _H_ac (1 kA/m) are shown in Fig.

1. A linear response without hysteresis was observed at _f_ = 100 kHz. Such superparamagnetic behaviour is reasonable because the estimated τ N(_H_ac = 0) for the nanoparticles is 20 ns.

Hysteresis appeared in the curves at _f_ = 1,000 kHz. As _f_ increased further, the area inside the hysteresis loop grew. This area corresponds to the work done in one cycle. Therefore,

_P_H/(_H_ac·_f _) also increased with _f_ and a single maximum was observed at a peak frequency, _f_p, of 10,000 kHz (Fig. 1 (b)). Figure 2(a) shows the _H_ac dependence using a contour plot

of _P_H/(_H_ac·_f _). As _H_ac increased, _f_p shifted towards higher frequencies. As indicated by the dashed line in Fig. 2(a), this shift can be explained by the values of τ N(_H_ac)

calculated using the conventional Brown's equation as follows12: where _h_ is _μH_/(2 _K_d_V_), _K_d is the shape anisotropy constant, _V_ is the volume of the magnetic core and _k_B is

the Boltzmann constant. Therefore, the emergence of a single peak in _P_H/(_H_ac·_f _) can be attributed to Néel relaxation loss, as expected for SPIONs. For the nearly spherical

nanoparticles with a low _H_ac (1 kA/m), the magnetisation curves in the rotatable case were the same as those in the non-rotatable case (see Fig. 1). An equivalent maximum appeared in the

_f_-dependence of _P_H/(_H_ac·_f _) in the linear response range (_H_ac = 1 kA/m) (Fig. 1(b)). This behaviour is consistent with the above assumption because the estimated τ N (_H_ac = 0) of

20 ns is much shorter than τ B = 8 μs (Table 1). The shift of this peak with increasing _H_ac is analogous to that in the non-rotatable case (Fig. 2(b)). However, another maximum of

_P_H/(_H_ac·_f _) was observed at _H_ac = 8−16 kA/m and _f_ = 30 kHz in the contour plot shown in Fig. 2(b). A secondary maximum like this has not previously been theoretically predicted for

individual monodisperse nanoparticles. Figure 3(a) shows the magnetisation curves calculated under these conditions. Unlike the non-rotatable case, an S-shaped hysteresis loop without

remanence existed. At the same time, the mean orientation of the long (easy) axes of the nanoparticles showed butterfly-shaped hysteresis, as shown Fig. 3(b). Because such behaviour cannot

be explained using the present linear response theory, its origin is discussed in the next section from the viewpoint of the rotation of the long axis of SPION. The magnetisation curves at

_f_ = 10,000 kHz for the elongated spheroidal nanoparticles, which are typical ferromagnetic nanoparticles, in the non-rotatable case are shown in Fig. 4(a). The curve was reversible at

_H_ac = 20 kA/m and hysteresis appeared in the curve at _H_ac = 26 kA/m. As _H_ac increased further, the area inside the hysteresis loop grew. When _H_ac became larger than 32 kA/m, the

expansion of the area was saturated and the shape of the magnetisation curve approached that predicted by the Stoner–Wohlfarth model. _P_H/(_H_ac·_f _) was almost zero at low _H_ac, then at

approximately 30 kA/m it began increasing rapidly with _H_ac, followed by a gradual decreases with increases in _H_ac (Fig. 4(b)). This behaviour depends weakly on the frequency (Fig. 5(a)).

In mechanical models that do not consider thermal fluctuation, a hysteresis loop appeared when _H_ac was higher than _H_sw. Because _H_sw of ferromagnetic nanoparticles with randomly

oriented easy axes ranges from _H_K/2 = 29 kA/m to _H_K = 57 kA/m and is often close to 0.5 _H_K, that _P_H/(_H_ac·_f _) is almost independent of frequency at _H_ac > 30 kA/m in the

non-rotatable ferromagnetic nanoparticles is consistent with the properties expected for the hysteresis loss. Figure 6 shows the magnetisation curves for rotatable elongated spheroidal

nanoparticles at _f_ = 10,000 kHz. Because the magnetic response slowly changed after the AC magnetic field was applied at _t_ = 0, transient variations of the hysteresis loops are observed.

The shape of the major hysteresis loop at _H_ac = 60 kA/m was initially consistent with that predicted by the Stoner–Wohlfarth model with randomly oriented easy axes. However, the remanence

of the major loop gradually increased from 0.5 _M_s to _M_s. In other words, the major loop became squarer and the area inside the loop increased with time. In comparison, the remanence of

the minor loop at _H_ac = 26 kA/m gradually decreased and the area became smaller over time. As shown in Fig. 6(c) and (d), the long (easy) axes of the nanoparticles gradually turned when

the variations of the loops proceeded (see the next section for details). Consequently, the increased area of the major hysteresis loops and decreased area of the minor loops caused the

maximum of _P_H/(_H_ac·_f _) to shift towards higher _H_ac compared with the non-rotatable case (see arrows in Fig. 4(b)). Note that reversals occurred every hundred nanoseconds (∼1/_f _),

while rotations took several microseconds (Fig. 6(c)). Thus, the assumption that the amount of hysteresis loss is unaffected by the rotation of nanoparticles when reversal is significantly

faster is invalid for ferromagnetic nanoparticles in large AC magnetic fields at high frequencies. Before discussing this novel phenomenon observed at high frequencies, the other important

variation in the contour plot of _P_H/(_H_ac·_f _) (Fig. 5) that occurred because of the ability of the ferromagnetic nanoparticles to rotate at lower frequencies shall be examined. The

maximum of _P_H/(_H_ac·_f _) shifted toward lower _H_ac below 100 kHz for the rotatable elongated spheroidal nanoparticles, while it stayed between _H_K/2 and _H_K in the non-rotatable case.

Figure 7(a) shows the magnetisation curve obtained when _H_ac = 16 kA/m and _f_ = 30 kHz. The curve in the rotatable case had an obvious hysteresis loop with a large remanence in the steady

state, but there was no hysteresis observed for the non-rotatable situation. Because _H_ac = 16 kA/m is much smaller than _H_K/2, no reversals of μ occur at any orientation of the easy axis

so hysteresis is not observed for the latter case. Figure 7(b) shows the variation of <cosθ> in the rotatable case, where <cosθ> (0 < _θ <_ π/2) is the mean angle between

the magnetic field and the long axes of the spheroidal nanoparticles. Note that <cosθ> is synchronised with |_M_/_M_s| = |cosψ|, where ψ is the angle between μ and _H_ . This fact

indicates that the hysteresis in the rotatable case (Fig 7(a)) is mainly caused by the rotation of the easy axis where the direction of μ is fixed. Consequently, heat equivalent to the

hysteresis loss dissipates even at _H_ac < _H_K/2. For Brownian relaxation, τ B can be expressed as follows: where η is the viscosity of the surrounding medium and _V_H is the

hydrodynamic volume. In equation (4), the frictional torque for spheroids, described in the Methods section, is considered. For the elongated spheroidal nanoparticle, (2πτ B)−1 is calculated

to be 8 kHz. This value is too low to cause the nanoparticle to rotate at 30 kHz. Therefore, Yoshida _et al._13 also took into account the rotation caused by magnetic torque, μ (_t_) × Η

(_t_). They concluded that the area of the hysteresis loop was maximised as follows: The location of the peak in _P_H/(_H_ac·_f _) below 100 kHz can be explained by this equation, as shown

in Fig. 5(b). An expression that describes all of the variation in the position of the primary peak of _P_H/(_H_ac·_f _) is desirable and equation (5) can be rewritten as follows: This

equation is an extended relationship of τ −1 = τ N−1 + τ B−1 for a large AC magnetic field. This expression is for the primary maximum; the secondary maximum is discussed later. The second

term of equation (6) can be approximated to 0.1_μH_ac/(_ηV_H) for _μH_ac/_k_B_T_ » (0.07)−0.5 and κ ∼ 1. On the other hand, τ N(_H_ac) of ferromagnetic nanoparticles becomes extremely short

only when the energy barrier disappears between _H_K/2 and _H_K. Therefore, the changeover between the two terms in the equation (6) generally occurs at _H_ac ≈ _H_K/2 and 2π_f_ ≈

0.1_μH_K/(2_ηV_H) = 0.1 _K_d_V_/(_ηV_H). For the elongated spheroidal particles (κ = 1.4, _K_d = 16 kJ/m3 and _V_/_V_H = 0.3) in a liquid phase with η = 1 mPa·s, the values of _H_ac and _f_

are 29 kA/m and 76 kHz. Such a changeover around 100 kHz occurs for ferromagnetic nanoparticles of any size, as long as the conditions, _K_d, _V_/_V_H and η, are constant. We must keep in

mind that, even when ferromagnetic nanoparticles are large enough for their Brownian relaxation to be negligible, the magnetic torque caused by the large AC magnetic field can easily rotate

such nanoparticles in the liquid phase at a time scale of microseconds. This knowledge is helpful when considering the frequency for hyperthermia treatment, even if it is obtained for a

simplified system. In summary, most of the simulated results, including significant variations for ferromagnetic nanoparticles exposed to a low-frequency AC magnetic field, can be explained

using the existing models. The two essential exceptions are as follows: * a a secondary maximum in the relaxation loss for SPIONs exposed to a low-frequency AC magnetic field and * b a shift

of the maximum hysteresis loss caused by the ability of typical ferromagnetic nanoparticles exposed to a high-frequency AC magnetic field to rotate. These novel phenomena are discussed in

detail in the following section. DISCUSSION The two novel phenomena of rotatable nanoparticles in a large AC magnetic field described above cannot be explained by simple models that consider

a linear response of thermodynamic equilibrium states or magnetic field-driven reversals. In this section, we shall further discuss these atypical responses from the viewpoint of the

orientation of the long (easy) axis. First, we begin with the appearance of a secondary maximum of _P_H/(_H_ac·_f _) near _H_ac = 8 kA/m and _f_ = 30 kHz for the nearly spherical

nanoparticles (typical SPIONs) where an S-shaped hysteresis loop without remanence was obtained (Fig. 3). We must recall that the variation in <cosθ> showed butterfly-shaped hysteresis

under these conditions. This behaviour explains the atypical magnetic response in the period _f_−1 (33 μs) (Fig. 3(b)). Initially (at _t_ = 0), no magnetisation exists because the

occupation probabilities of μ in the two stable directions parallel to the long (easy) axis are equalised in a zero magnetic field. As _H_ increases, the occupation probability in the more

stabilised direction immediately increases because of reversals on a time scale of τ N (≤ 20 ns). The reversed μ in the stabilised direction is not completely parallel to _H_ , ψ ≠ 0 and the

magnetic torque _μH_sinψ turns the long (easy) axis towards the direction of the field. If we neglect Brownian torque λ (_t_) (see equation (11) in the Methods section), the angular

velocity of the rotation due to magnetic torque can be expressed as Hence, ω H(_H_(_t_), ψ(_t_)) increases in proportion to the field amplitude _H_ = _H_acsin(2π_f_·_t_). For example, ω

H(_H_, ψ = π/4) is 0.15×106 rad/s when _H_ (_t_ = 1/4_f_ ≈ 8 μs) is 8 kA/m. Therefore, rotation is not negligible in the peak period of the oscillations of _H_. Subsequently, _H_ decreases

to zero at _t_ = 1/2_f_ ≈ 17 μs and the occupation probabilities are again equalised because reversal is rapid, so the magnetic torque disappears. Alternatively, the Brownian torque

randomises the orientation of the long axis on a time scale of τ B ( = 8 μs). Therefore, competition between the magnetic and Brownian torques can cause the butterfly-shaped hysteresis of

<cosθ>. Because the equilibrium magnetisation of SPIONs with easy axes parallel to _H_ is higher than that of randomly oriented SPIONs14, the magnetisation curve shows hysteresis

without remanence. Consequently, a secondary maximum appears for the rotatable SPIONs even though τ N « τ B. Next, we investigate the influence of the ability of elongated spheroidal

nanoparticles to rotate under a high-frequency AC magnetic field on the shift of the maximum _P_H/(_H_ac·_f _). As shown in Fig. 6(a) and (b), the magnetisation curves varied after an AC

magnetic field was applied at _t_ = 0. At the same time, transient variations also occurred in <cosθ>, as shown in Fig. 6(c). In the case of the major loop at _H_ac = 60 kA/m,

<cosθ> gradually increased from 0.5 to 0.95. In other words, the long (easy) axis became oriented towards the direction parallel to _H_ . The characteristic time, τ rot, was estimated

to be 1.3 μs using the approximation of exponential decay. Note that the direction of μ is not completely parallel to _H_ even for _H_ ≥ _H_K, even though μ is already reversed for all of

the nanoparticles. Because sin ψ is 0.43 when cos ψ is 0.9, a large magnetic torque can turn the long axis even if the magnetisation is almost saturated after reversals at _H_ ∼ _H_K.

Indeed, τ rot at _H_ac ≥ _H_K is comparable to the reciprocal of typical values of ω H(_H = H_ac, sin ψ = 0.43) (Fig. 6(d)). Therefore, these transient variations can be attributed to the

longitudinal orientation being adopted preferentially because of the magnetic torque. In the minor loops at _H_ac = 26 kA/m, the remanence of the rotatable nanoparticles decreased gradually

with time (Fig. 6(b)) and <cosθ> simultaneously decreased from 0.5 (Fig. 6(c)). The long axis was oriented perpendicular to _H_ during this period, although the longitudinal

orientation is preferred when the Zeeman energy is considered. It should be noted that the angle ψ for μ in a stable direction more parallel to _H_ is smaller than that in a metastable

direction less parallel to _H_ (Fig. 6(d)). In other words, the magnitude of the magnetic torque toward the longitudinal orientation in the former is weaker than that toward the

perpendicular orientation in the latter. This difference makes the orientation of the long axis planar on average, because the stable and metastable states alternate every half period when

the reversal of μ is blocked in the minor loop. These arguments suggest that the slowing of the rotation for 0.5 _H_K ≤ _H_ac ≤ _H_K (Fig. 6(d)) can be attributed to compensation between two

magnetic torques in the intermediate range. Briefly, in ferromagnetic nanoparticles in the aqueous phase, longitudinal or planar orientations are adopted, irrespective of the free energy,

as dissipative structures under a high-frequency AC magnetic field. Consequently, _P_H/(_H_ac·_f _) increases gradually in major hysteresis loops and decreases in minor loops. These

variations cause the maximum of _P_H/(_H_ac·_f _) to shift towards higher _H_ac. Finally, we return to the contour plots of _P_H/(_H_ac·_f _) in Figs. 2 and 5 and discuss the effect of

rotation on the design for maximising _P_H/(_H_ac·_f _). If a safety limit of _H_ac·_f_ < 4.85×108 Am−1s−1 is applied9, then maximum values of _P_H/(_H_ac·_f _) for rotatable SPIONs and

ferromagnetic nanoparticles are obtained at the conditions shown by diamonds A and C in Figs. 2(b) and 5(b), respectively. However, no heat dissipation occurs under the same conditions (A

and C) if the rotation of these nanoparticles is blocked (Figs. 2(a) and 5(a)). If a highly amplified AC magnetic field _H_ac·_f_ of 1.74×1010 Am−1s−1 is allowed15, a maximum _P_H/(_H_ac·_f

_) of 3.0×10−4 m−3s−2A−1 (5.2 MW/kg) for the rotatable ferromagnetic nanoparticles can be obtained (diamond D in Fig. 5(b)). However, _P_H/(_H_ac·_f _) halves when the rotation of these

nanoparticles is blocked (Fig. 5(a)) because oriented structures are not formed. In contrast, condition B for the primary maximum of _P_H/(_H_ac·_f _) in the rotatable SPIONs remains the

optimum condition when these nanoparticles cannot rotate (Fig. 2(a) and (b)). This is because the long (easy) axes of SPIONs are randomly oriented in rotatable SPIONs as Brownian torque has

more effect than magnetic torque in a weak magnetic field. As demonstrated here, rotation generated by the magnetic torque caused by a large alternating magnetic field greatly affects the

conditions for maximising heat dissipation in magnetic nanoparticles. In this study, we simulated the magnetic responses of superparamagnetic and ferromagnetic magnetite nanoparticles in a

large alternating magnetic field. The results show that both the relaxation loss for τ N « τ B and the hysteresis loss at _H_ac ≈ _H_sw are affected by the formation of dissipative

structures because of the ability of nanoparticles to rotate. Consequently, the conditions for maximising heat dissipation depend strongly on the inhomogeneous microviscosity of the

surrounding medium. Compared with the simplified model used for our simulation, actual magnetic nanoparticles used for targeted magnetic hyperthermia treatment are not ideal. For this

reason, the factors affecting more realistic situations need to be evaluated. First, the effects of crystalline and surface anisotropy energy are considered. In this case, the potential

energy with respect to the direction of μ is complicated. Even if multiple valleys appear in the energy surface, the easy axes are not parallel to _H_ , because the orientations of the

nanoparticles are randomised by Brownian torque in the liquid phase. For this reason, slow rotations inevitably occur after fast reversals because of the magnetic torque in an AC magnetic

field. These rotations lead to secondary relaxation loss in SPIONs in a low frequency AC magnetic field and shift the hysteresis loss in ferromagnetic nanoparticles in a high frequency AC

magnetic field. Next, the variation in the size and shape of actual nanomagnets must be considered. In this case, Néel relaxation times, τ N, differ significantly because they depend

exponentially on the volume of each nanoparticle and the shape anisotropy constant. In contrast, the dependence of frictional torque on the size and shape of nanoparticles is weak. Because

the S-shaped hysteresis loop of SPIONs appears in the frequency range of rotation, the secondary loss peak becomes less diffuse compared with the primary relaxation loss peak. For

ferromagnetic nanoparticles, the shift of the hysteresis loss at high frequencies should still be significant even if the size of nanoparticles is not uniform, because the anisotropy field

is independent of nanoparticle size. Finally, the effect of dipole–dipole interactions is considered, because the density of nanoparticles accumulated in cancer cells might be inhomogeneous

if they are trapped at specific sites. In such a case, chain structures of longitudinally aligned nanoparticles have been conventionally discussed in a magnetic field, although their details

are still controversial16. Our findings illuminate this conventional view, because, in some cases, formation of structures with a planar orientation is predicted even for individual

ferromagnetic nanoparticles. In future studies, we will clarify a variety of dissipative structures, which are different from ordinary chains, for interacting nanoparticles. As discussed

here, knowledge of the heat dissipation in the non-equilibrium steady states of rotatable nanoparticles is essential for the design of targeted magnetic hyperthermia treatments using large

AC magnetic fields. METHODS MODEL FOR THE SIMULATION The magnetic response to an AC magnetic field _H_acsin(2π_f_·_t_) was simulated for individual superparamagnetic/ferromagnetic magnetite

nanoparticles in two extreme cases: non-rotatable nanoparticles strongly anchored to structures resembling organelles and rotatable nanoparticles in an aqueous phase resembling the

cytoplasm. We considered the nanoparticles to be monodisperse prolate spheroids with equatorial diameters, 2_R_M, from 12 to 24 nm and aspect ratios, κ, between 1.1 and 1.4. Because these

dimensions are smaller than the typical exchange length of magnetite, 27 nm,17 all of the spins are parallel to one another in each nanoparticle. In other words, we can assume that each

nanoparticle has a single magnetic moment μ = _M_S_V_ (coherent rotation/ macro-spin approximations14), where _V_ is the volume of each nanoparticle, [(4/3)π·_κR_M3]. The magnitude of

spontaneous magnetisation _M_s = | _M_s| was set to the value of bulk magnetite6, 450 kA/m, because the dependence of _M_s on particle size has not been well established18. The magnitude of

μ is important; for example, μ of a nanoparticle with 2_R_M = 24 nm and κ = 1.4 is 1.5×105 μ B. Hence, such nanoparticles aggregate because of the large dipole–dipole interactions between μ

unless a sufficient non-magnetic surfactant layer exists. The required thickness of this layer is approximately 6 nm for nanoparticles with 2_R_M = 24 nm19. Therefore, in our model, we used

non-magnetic layers with a thickness _δR_ of 0.5 _R_M. Consequently, we can assume that the nanoparticles are uniformly dispersed and do not aggregate. In this case, the typical distance

between nanoparticles is _n_–1/3, where _n_ is the number density of nanoparticles. Because the actual mass fraction of nanoparticles accumulated in cancer cells does not exceed 1%

(approximately 10 mg/mL), the magnitude of the interaction between nanoparticles with 2_R_M = 24 nm, _n_·μ 2/_k_B, is estimated to be less than 1×102 K. Consequently, we did not consider

minor effects caused by dipole–dipole interactions in our simulations. In such an individual nanoparticle, the potential energy with respect to the direction of μ , _U_(Ω), is given by the

following equation: where _U_d(Ω), _U_c(Ω), _U_s(Ω) and − _Μ·H_ are the shape, crystalline and surface anisotropy energies and Zeeman energy, respectively and Ω is the solid angle of μ . For

spheroidal particles, the first term, _U_d(Ω), can be described as _K_d_V_sin2 φ and has two minima separated by the energy barrier Δ_U_ = _K_d_V_, where _K_d is the shape anisotropy

constant and φ is the angle between the long (easy) axis and μ . The magnitudes of _K_d, given by (_N_easy–_N_hard)μ 0·_M_s2, are 5 and 16 kJ/m3 for spheroidal particles with κ of 1.1 and

1.4, respectively. _N_easy and _N_hard are the demagnetising factors for the long and short axes, respectively. In comparison, magnetite has cubic crystalline anisotropy20 and an anisotropy

constant _K_1 = −11 kJ/m3. The energy landscape of cubic anisotropy (_K_1_<_0) is gentle and Δ_U_ is (1/12)_K_1_V_ ≈ (1 kJ/m3)·_V_19. Additionally, the effects of surface anisotropy are

generally insignificant if the particles are larger than 10 nm18, although the rationale for this is still unknown. For these reasons, we assumed that the uniaxial shape anisotropy

dominated. Consequently, equation (8) can be simplified as follows: where ψ is the angle between μ and _H_ (see Fig. 3). Little is known about the local environments of magnetic

nanoparticles accumulated in tumour tissue. For example, nanoparticles coated with dextran are completely immobilised in tissues21, whereas dextran nanoparticles appear to be mobile in

cells5. For this reason, we simulated the magnetic response of the monodisperse spheroidal nanoparticles in the following two extreme cases: non-rotatable nanoparticles with randomly

oriented easy axes and rotatable nanoparticles in a Newtonian fluid with a viscosity η of 1 mPa·s.4 SIMULATION OF THE REVERSAL The detailed trajectories of μ in a magnetic field applied at

an oblique angle θ to the long easy axis of a spheroidal particle can be precisely simulated by solving the stochastic Landau–Lifshitz–Gilbert equations. However, we are only interested in

the reversal of μ once every microsecond because the frequency used for hyperthermia is limited. Therefore, we can use a well-known coarse-grained approach, or “two-level approximation”14,

that considers thermally activated reversals between the meta-stable directions, (φ 1, ψ 1) and (φ 2, ψ 2), _via_ the midway saddle point at (φ 3, ψ 3) in _U_θ(φ,ψ). The reversal probability

from (φ 1, ψ 1) to (φ 2, ψ 2), υ 12, is given by _f_0–1·exp[(_U_θ(φ 3, ψ 3) − _U_θ(φ 1, ψ 1))/_k_B_T _], while the backward reversal probability υ 21 is _f_0–1·exp[(_U_θ(φ 3, ψ 3) − _U_θ(φ

2, ψ 2))/_k_B_T _], where _f_0 is the attempt frequency of 109 s–1. In the simulation, the time evolution of the occupation probabilities, _p_1(θ)_, p_2(θ) = 1 − _p_1(θ), at the two stable

directions of a nanoparticle tilted at θ was computed using the following relationship: _p_1(θ) was simply set to either zero or one when there was only one minimum in _U_θ(φ,ψ). This

calculation was continued until the transient factors depending on the initial conditions disappeared. The time step _Δt_ was typically 10−4/_f_ s but was shorter when υ 12_Δt_ (or υ 21_Δt_)

became large compared with one. At each step, magnetisation was obtained as ∫(_p_1(θ)μcosψ 1 _+ p_2(θ)μcosψ 2)sin_θdθ_. Test simulations were performed to check the validity of this method

using the same parameters as in an earlier study14 to calculate the reversals of magnetic nanoparticles in large AC magnetic fields. As detailed in the Supplementary Information, our results

agree with the reported behaviour14. SIMULATION OF REVERSAL AND ROTATION The rotation of spheroidal nanoparticles was simulated in synchronisation with the reversal of μ . In Newtonian

fluids, the frictional torque for rotation can be expressed as 6_ηV_H·(0.8 + 0.2κ)· ω (_t_),22 where _V_H = [(4/3)π·κ(_R_M + _δR_)3] is the hydrodynamic volume and ω (_t_) is the angular

velocity of rotation; d _E_ /d_t_ = ω (_t_) × _E_ (_t_), where _E _ (_t_) is the unit vector along the long axis of the spheroid; and μ (_t_)· _E_ (_t_) = μcosφ. Under typical conditions,

where η = 1 mPa·s, _V_H ≈ 103 nm3 and ω(_t_) ≈ 1×105 rad/s, the inertia of the nanoparticle can be neglected (Brownian dynamics simulation). In this inertia-less limit23, the frictional

torque balances with magnetic torque μ (_t_)× _H_ (_t_) and Brownian torque λ (_t_) as follows: where δ(t1−t2) is the Dirac delta function. At the beginning of the simulation for the

rotatable nanoparticles, an assembly of randomly oriented nanoparticles was generated, where their number ensures an optimal compromise between calculation time and precision. Then, the time

evolution of the direction of μ and the orientation of the long easy axis were computed by the following steps. (i) Using equation (9), reversible variations of the meta-stable directions

(φ i(_t_), ψ i(_t_)) caused by the latest changes in the field strength and direction of the easy axis were calculated, (ii) μ (_t_) at (φ 1(_t_), ψ 1(_t_)) was reversed if _x_ < υ

12_Δt_, but otherwise not. In this case, _x_ ∈ [0, 1] is a pseudorandom number generated by the Xorshift algorithm24. The backward reversal was computed in a similar manner. (iii)

Substituting the reversed (or held) μ (_t_) into equation (11), ω (_t_) was calculated. (iv) _E_ (_t_) was finally computed using the relationship d _E_ /d_t_ = ω (_t_)× _E _ (_t_). This

calculation was continued until transient factors depending on the initial conditions disappeared. In this simulation, _Δt_ was typically 10−4/_f_ s but was shorter unless υ 12_Δt_, or the

changes in _E _ (_t_) were sufficiently small compared to one. Magnetisation was obtained as Σ(_n_i μcosψ i) at each step. Test simulations were performed to check the validity of this

method. There have been no prior theoretical studies on systems where both reversal and rotation occur simultaneously in a large AC magnetic field. Consequently, comparisons with prior

studies were performed under two extreme conditions. In the first case, high viscosities were assumed. Because reversal dominates rotation under these conditions, the results were compared

with those reported by Carrey _et al_.14. In the second case, a high anisotropic field was assumed. Because rotation dominates reversal in this situation, the results were compared with the

numerical simulations of Yoshida _et al_., where nonlinear Brownian rotational relaxation of magnetic fluids with a large excitation field was studied using the Fokker–Planck equation13. The

results obtained from our simulation of reversal and rotation were consistent with those of earlier studies (Supplementary Figs. S1–S4). Therefore, we can now take a first step toward

understanding the roles that rotation of a nanoparticle and reversal of its magnetic moment play together in large AC magnetic fields. REFERENCES * Pankhurst, Q. A., Thanh, N. K. T., Jones,

S. K. & Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D42 224001 (2009). * Sugahara, K. N., et al. Coadministration of a tumor-penetrating

peptide enhances the efficacy of cancer drugs. Science 328, 1031–1035 (2010). Article  CAS  ADS  Google Scholar  * DeNardo, S. J., et al. Development of Tumor Targeting Bioprobes

(111In-Chimeric L6 Monoclonal Antibody Nanoparticles) for alternating magnetic field cancer therapy. Clin. Cancer Res. 11, 7087s–7092s (2005). Article  CAS  Google Scholar  * Kuimova, M. K.,

et al. Imaging intracellular viscosity of a single cell during photoinduced cell death. Nature Chem. 1, 69−73 (2009). Article  CAS  ADS  Google Scholar  * Kalwarczyk, T., et al. Comparative

analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale. Nano Lett. 11, 2157–2163 (2011). Article  CAS  ADS  Google Scholar  * Rosensweig, R. E. Heating

magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 252, 370–374 (2002). Article  CAS  ADS  Google Scholar  * Chung, S. -H., _et al_. Biological sensing with magnetic

nanoparticles using Brownian relaxation. J. Appl. Phys. 97, 10R101 (2005). Article  Google Scholar  * Kalele, S., Narain, R. & Krishnan, K. M. Probing temperature-sensitive behaviour of

pNIPAAm-coated iron oxide nanoparticles using frequency-dependent magnetic measurements. J. Magn. Magn. Mater. 321, 1377–1380 (2009). Article  CAS  ADS  Google Scholar  * Hergt, R., Dutz, S.

& Röder, M. Effects of size distribution on hysteresis losses of magnetic nanoparticles for hyperthermia. J. Phys.: Condens. Matter 20, 385214 (2008). * Kim, D.-H., Nikles, D. E.,

Johnson, D. T. & Brazel, C. S. Heat generation of aqueously dispersed CoFe2O4 nanoparticles as heating agents for magnetically activated drug delivery and hyperthermia. J. Magn. Magn.

Mater. 320, 2390–2396 (2008). Article  CAS  ADS  Google Scholar  * Müller, R., et al. Hysteresis losses in iron oxide nanoparticles prepared by glass crystallization or wet chemical

precipitation. J. Magn. Magn. Mater. 310, 2399–2404 (2007). Article  ADS  Google Scholar  * Brown, Jr, W. F. Thermal Fluctuations of a Single-Domain Particle. Phys. Rev. 130, 1677–1686

(1963). Article  ADS  Google Scholar  * Yoshida, T., & Enpuku, K. Simulation and Quantitative Clarification of AC Susceptibility of Magnetic Fluid in Nonlinear Brownian Relaxation

Region, _Jpn_ . J. Appl. Phys. 48, 127002 (2009). Article  Google Scholar  * Carrey, J., Mehdaoui, B., & Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic

single-domain nanoparticles: Application to magnetic hyperthermia optimization, _J. Appl_ . Phys. 109, 083921 (2011). Google Scholar  * Fortin, J. P., et al. Size-sorted anionic iron oxide

nanomagnets as colloidal mediators for magnetic hyperthermia, _J. Am_ . Chem. Soc. 129, 2628−2635 (2007). * Mamiya, H., Nakatani, I., & Furubayashi, T. Phase transitions of iron nitride

magnetic fluids, _Phys_ . Rev. Lett. 84, 6106−6109 (2000). Article  CAS  ADS  Google Scholar  * Li, Z., Kawashita, M., Araki, N., Mitsumori, M., Hiraoka, M. & Doi, M. Magnetite

nanoparticles with high heating efficiencies for application in the hyperthermia of cancer. Mater. Sci. Engineering, C 30, 990–996 (2010). Article  Google Scholar  * Demortière, P., et al.

Size-dependent properties of magnetic iron oxide nanocrystals. Nanoscale 3, 225−232 (2011). Article  ADS  Google Scholar  * Mamiya, H., & Jeyadevan, B. Optimal design of nanomagnets for

targeted hyperthermia _J. Magn_ . Magn. Mater. 323, 1417–1422 (2011). Article  CAS  ADS  Google Scholar  * Hellwege, K. H. Magnetic and Other Properties of Oxides and Related Compounds,

(Landolt-Börnstein New Series III 4B, Springer-Verlag, New York, 1970). * Dutz, S., Kettering, M., Hilger, I., Müller, R., & Zeisberger, M. Magnetic multicore nanoparticles for

hyperthermia—influence of particle immobilization in tumour tissue on magnetic properties,. Nanotechnology 22, 265102 (2011) Article  ADS  Google Scholar  * Ilg, P. & Kröger, M.

Magnetisation dynamics, rheology and an effective description of ferromagnetic units in dilute suspension. Phys. Rev. E66, 021501 (2002). ADS  Google Scholar  * Coffey, W. T. On the

contribution of multiplicative noise terms to the Langevin equation for rotational relaxation. J. Chem. Phys. 99, 3014–3020 (1993). Article  CAS  ADS  MathSciNet  Google Scholar  *

Marsaglia, G. Xorshift RNGs, _J. Stat_ . Soft. 8, 1–6 (2003). Google Scholar  Download references ACKNOWLEDGEMENTS This study was partly supported by a Grant-in-Aid for Scientific Research

(21241023 and 21681014). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * National Institute for Materials Science, Tsukuba, 305-0047, Japan Hiroaki Mamiya * The University of Shiga Prefecture,

Hikone, 522-8533, Japan Balachandran Jeyadevan Authors * Hiroaki Mamiya View author publications You can also search for this author inPubMed Google Scholar * Balachandran Jeyadevan View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H. M. performed the simulation. H. M. and B. J. wrote the manuscript. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing financial interests. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION Supplementary materials RIGHTS AND PERMISSIONS This work

is licensed under a Creative Commons Attribution-NonCommercial-NoDerivative Works 3.0 Unported License. To view a copy of this license, visit

http://creativecommons.org/licenses/by-nc-nd/3.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mamiya, H., Jeyadevan, B. Hyperthermic effects of dissipative structures of

magnetic nanoparticles in large alternating magnetic fields. _Sci Rep_ 1, 157 (2011). https://doi.org/10.1038/srep00157 Download citation * Received: 08 July 2011 * Accepted: 28 October 2011

* Published: 15 November 2011 * DOI: https://doi.org/10.1038/srep00157 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link

Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative