News Reader.info

ABSTRACT Biomembranes shown to behave like elastic sheets, can also suffer plastic deformations. Neutron scattering experiments on partially polymerised wrinkled membranes revealed that when

a critical degree of polymerisation is crossed, the wrinkled membranes do not resume their spherical shapes. Instead they remain wrinkled and rigid while their non-polymerised counterparts

resume their spherical floppy shapes. The yield stress of these membranes, measured for the first time via the fractal dimension, is intimately related to the degree of polymerisation

probably through a 2D disorder that quenches the lateral diffusion of the lipid molecules. This work might shed light on the physical reason behind the irreversible deformation of

echinocytes, acanthocytes and malaria infected red blood cells. SIMILAR CONTENT BEING VIEWED BY OTHERS SURFACE MODEL OF THE HUMAN RED BLOOD CELL SIMULATING CHANGES IN MEMBRANE CURVATURE

UNDER STRAIN Article Open access 01 July 2021 CORRELATED FLICKERING OF ERYTHROCYTES MEMBRANE OBSERVED WITH DUAL TIME RESOLVED MEMBRANE FLUCTUATION SPECTROSCOPY UNDER DIFFERENT D-GLUCOSE

CONCENTRATIONS Article Open access 28 January 2021 EXACT SOLUTIONS FOR THE WRINKLE PATTERNS OF CONFINED ELASTIC SHELLS Article 25 August 2022 INTRODUCTION Lipid membranes mimic red blood

cells (RBC) albeit in an oversimplified way. Besides the lipid bilayer, RBC possess a spectrin mesh for extra shear-resistance. Malaria, acanthocytosis and echynocytosis are examples of

pathologies in which RBC suffer deformations that are due to defects in the spectrin network, such as dissociation in the case of malaria, which induces a permanent shape change1 or a

symmetry breaking between the two leaflets of the lipid membrane in the case of acanthocytes2. The mechanics of lipid membranes were modeled using an elastic formalism borrowed from elasic

sheets3,4 but so far no plastic behavior has been observed nor documented. Plasticity is often attributed to dislocation dynamics in metals5 and to volume increases in polymers6. It is,

however, not clear whether plastic deformations are the result of such kinematics and flows or if they cause them. Stress condensation on ridges7 and vertices8 during the crumpling process

of thin sheets is an example of when the onset of elastoplasticity is induced by volume reduction9,10. Whereas crumpling of thin sheets has emerged as an archetype of disordered systems, the

aforementioned studies focused on elastic behavior, which restricts the richness of these systems. Large deformations, however, induce real-life sheets to behave plastically. Elastic

crumpling is characterized by a hierarchical cascade during which large folds break into smaller folds until compaction11. At “weak” confinement, the competition between bending and

stretching dominates the self-avoidance of the sheet, whereas at stronger confinement, when making a ball of radius _R_, for instance, the sheet's self-avoidance hinders the formation

of smaller folds12. The interplay between self-avoidance and elasticity manifests itself in the Flory relationship, an important result from polymer physics, which states that the radius,

_R_, of the crumpled configuration scales with the size of the system, _L_, such that , where ν is the Flory exponent and _d__F_ is the fractal dimension that measures how the sheet's

size affects the mechanical compaction. This result holds for crumpling at a constant force and the identity ν = 2/_d__F_ is for maximally compacted two-dimensional surfaces and holds for

different materials13,14,15,16. For elastic sheets, _d__F_ ~ 2.5. For plastically deformed macroscopic sheets this relationship holds but with a different exponent ν and _d__F_ < 2.517.

At the micro- and nanoscales, conformations of crumpled graphite oxide sheets were probed experimentally using light and X-rays scattering and the fractal dimension was found to be that of

deformed elastic sheets with _d__F_ ~ 2.518,19. Membranes, made of partially polymerized diacetylenic phospholipids and cooled below the chain melting temperature, _T__m_, undergo a

thermodynamic wrinkling transition, similar to the wrinkling of an elastic macroscopic sheet, where the vesicles abruptly fold, wrinkle, collapse and expel their payload20,21. Atomic Force

Microscope (AFM) profilometry on these crumpled lipid membranes revealed that their surfaces were self-similar and behaved like elastic sheets up to the degree of polymerization after which

the roughness exponent fell into a different universality class also called a glassy phase21. The mechanics that describe this phase are still lacking however. Furthermore, profilometry only

probes the envelope of the surface of the wrinkled membrane and does not access the convoluted three-dimensional (3D) conformation of the membrane nor does it give sufficient information on

the local mechanics of the wrinkled membrane. To probe the mechanical behaviour of these membranes we use a scattering technique. Since X-rays uncontrollably polymerise the membranes, we

used neutron scattering to gain access to the local structure while measuring the fractal dimension of these self-similar structures18. The scattering intensity is proportional to the

structure factor , where _g_(_r_) is the pair correlation function, which is a power law for a fractal object and for and for 22,23,24. Small Angle Neutron Scattering at the Argonne National

Laboratory (Illinois) enabled us to probe length-scales from 15 to 1500 Å such that , where R is the size of the vesicle (on the order of tens of microns) and 1/_Q_ is the observation

scale. We expected that if the wrinkled membranes were self-similar and fractal, the scattered intensity would be expressed as a power-law in _Q_. (Data analysis is explained in the section

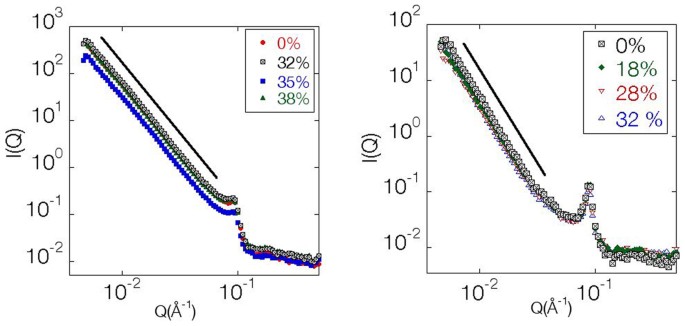
Materials and Methods). RESULTS Figure 1 left panel presents the plot of the scattered neutron intensity versus the wavenumber for lipid tubules dispersed in water. As shown in the figure,

when _Q_ is smaller than 0.1 Å−1, the data from all samples fall on a line best fitted to the function , where _d__F_ is the fractal dimension. It is a constant and approximately equal to 3,

within experimental error, which is characterestic of mass fractals25. Around , the intensity has a local peak at _Q_ = 0.094 Å−1 after which it drops, following a power law of the form

_Q_−4 corresponding to the Porod regime for sharp interfaces26. This partial peak corresponds to an interlayer distance of 6.68 nm for tubules in the crystalline phase where the bilayers

consist of tilted chain-frozen lipids. This value agrees with previous results using X-rays27. When the tubules are heated to 45°C, they swell into vesicles with a characteristic bilayer

thickness given by the peak in the intensity at Q = 0.088 Å−1 as shown in Figure 1 right panel. This peak's position, which does not depend on the degree of polymerization, corresponds

to an interlayer distance, _d_ = 7.14 nm higher than twice the lipid chain length. We systematically varied the degree of polymerization and captured the scattering spectra from the

membranes. Figure 2a shows the intensities from vesicles with low and high degrees of polymerization when the temperature was kept at 15°C. Unlike the plots in Figure 1-left panel, the slope

of the intensity spectrum for _Q_ < 0.1Å−1 shows a clear dependence on the degree of polymerization. The fractal dimension, retrieved from the slopes for different degrees of

polymerization and shown in Figure 2b, remains constant at around 2.5 over a wide range of degrees of polymerization. At a critical degree of polymerization ϕ_c_ ~ 30% it drops reaching the

value of 2.05 when ϕ ~ 40%. This behavior of _d__F_ is similar to the behavior of the roughness exponent for these membranes21. The surfaces for which _d__f_ < 3 are clearly different

from rough surface fractals (3 < _d__F_ < 4) or mass fractals (), however. One wonders about the mechanism behind the drop in the value of the fractal dimension when the degree of

polymerization crosses a critical value. Step IV in Figure 3 demonstrates our new capability to heat the dispersed wrinkled vesicles beyond _T__m_. When crumpled vesicles that were

polymerized below 30% were heated beyond _T__m_, they recovered their spherical shapes. Their corresponding intensities are given in the bottom curve in Figure 2c. Crumpled vesicles that are

polymerized above 30% and heated beyond _T__m_ had the same scattering intensity as the ones kept at low temperature as shown in Figure 2d. The absence of the interlayer peak and the

presence of a cross-over at _Q_ ~ 0.1 is inherent in a typical thickness with defects in the membrane. Similar cross-overs have been observed in the spectrin networks of red blood cells

(RBCs) when probed with light and X-ray scatterings28. At polymerizations beyond a critical value ϕ_c_ ~ 30%, the vesicles that are heated to temperatures around 45 or 50°C do not recover

their spherical shapes anymore as shown by the scattering intensity shown in Figure 2d, where the acquisition lasted for 12 hours, as well as by phase contrast microscopy. They were indeed

locked in a wrinkled configuration via plastic deformation. The representative peaks observed at higher temperatures disappear and the intensity plots are similar with equal slopes equal to

2.25. The vesicles do not unwrinkle and stay trapped in a plastic state. The plots in (3-a) and (3-d) are offset vertically for clarity. DISCUSSION As mentioned above, lipid membranes are

well described using continuum elasticity theory. Previous experiments on membranes and graphene sheets revealed that their behaviour is universal and scale independent – lipid membranes

behave just like macroscopic elastic sheets. Given the plethora of numerical studies that use continuum mechanics to describe lipid membranes29, it is then justifiable to extend results from

numerical studies on macroscopic sheets to microscopic sheets such as lipid membranes. Recent numerical simulations30, in which a thin sheet of lateral dimension _L_ was packed and crumpled

into a ball of radius _R_ under constant force, showed that if the scaling behavior holds, the fractal dimension depends weakly on the applied crumpling force. These simulations further

showed that when the material was purely elastic, _d__F_ = 2.5 remained constant; when the material was elastoplastic however, the fractal dimension decreases from 2.5 to lower values,

approaching 2, with the yield stress, σ_y_, also decreasing. Similar trend was found in real crumpled plastic foils that were experimentally folded into balls17. We recall that the Flory

exponent, ν, which relates the lateral dimension to the size of the confining space or the packed configuration through _R_ ~ _L_ν, is related to the fractal dimension, for maximum packing

only, via the relation ν = _D_/_d__F_, where _D_ = 2 is the dimension of the sheet14. Our observations here allow us to draw various conclusions. Figure 2b shows that the membrane has

properties similar to an elastic sheet (i.e. mylar or graphene18) at low degrees of polymerisation and to that of a plastic sheet (i.e. aluminum foil17) at high degrees of polymerisation.

Thus, the two distinct states we observed are related to the transition from elastic to elastoplastic behavior. Moreover, increasing the degrees of polymerization causes the membrane to

behave elastoplastically and the yield stress becomes a decreasing function of the degree of polymerization, σ_y_/_E_ = _f_(ϕ), where _E_ is the Young's modulus. Based on the analogies

above and that lipid membranes have similar behaviour to macroscopic elastic sheets, we can estimate the value of the yield stress for these polymerised membranes by comparing the values of

the fractal dimension for a given yield stress reported in30 to the fractal dimensions reported in this study. In30 the universality of the folding pattern was a function of the ratio of the

length of the sheet to its thickness which indicates that the scale of the sheet is irrelevant as long as the ratio of the folds to the bilayer's thickness is above 100. The

non-universality and the dependence of the crumpling on this ratio was attributed to plastic yielding. We find that (ϕ; σ_y_/_E_) = (35%;0.05), (36.8%;0.01), (39%;0.002). While the

elastoplasticity of macroscopic objects has been characterized in three dimensions only, it is possible to relate elastoplasticity to glassy behavior at the microscopic level in lipid

membranes31 where defects (disclinations or dislocations) created by the polymerization cause the membrane to behave like a plastic solid32. Also and as shown before and using generalised

polarisation measurements21, the wrinkling temperature depends on the degree of polymerisation. This is possibly due to a competition between the local intrinsic strain which originates from

the polymer network and gives rise to a non-zero gaussian curvature and the possible configurations of the lipids. Although we submitted the vesicles to constant loading [_T_1 ↔ _T_2], the

wrinkling occured at a temperature that was never below 15°C. We have compared the fractal dimension values with the values of the roughness exponents and we found a slight correlation

beyond the critical polymerization, which we believe is merely coincidental, but surprisingly no correlation below the critical polymerization where both exponents are constant. This could

be expected since the roughness exponent measured using AFM underestimated the mechanics of the folding process during the wrinkling which gives rise to an area that is larger than the

effective surface measured by the AFM. For rough surfaces generated from fracture for example, the two exponents are linearly dependent33. We now focus on the power-law dependence of the

fractal dimension on the degree of polymerisation. According to Figure 2b, and _d__F_ ~ ϕ−1/2. The dependence of the fractal dimension on ϕ means that the elastic moduli depend on ϕ. As a

first approximation, we assume the Ansatz that _K_ ~ _k__B__Tϕ_, where _K_ is the splay modulus34. _I_(_Q_) is proportional to the neutron scattering structure factor, _S_(_Q_), which is

proportional to the density-density correlation function. If the Hamiltonian used to calculate the correlation function is a function only of the Lamé coefficients as in the case of a

crystalline membrane or contains only a bending term, the correlation function behaves like a power-law with the exponent depending linearly on the elastic constant35. For the exponent to

depend on ϕ1/2, the elastic modulus must have the same exponent within the above approximation. As shown earlier, the bilayer becomes compressed when the vesicles are cooled. This suggests

that, when calculating the correlation function, we should use the Landau-Peierls Hamiltonian that describes the compression of a smectic-A that accompanies splay36. This Hamiltonian

contains a compression term and is proportional to the compressibility of the layers, _B_(_∂u_/_∂z_)2, as well as a bending term, _K_(∂2_u_/_∂x_2 + ∂2_u_/_∂y_2)2. The membranes being

polymerized would experience extra stretching on the outer layer like an accordion. Since the membrane is not fully polymerized, we do not need to introduce the Lamé coefficients. If we use

this Hamiltonian to calculate the intensity, we find that , where . Since , then . It is also possible that the polymer is inducing an unbinding transition of the bilyaer which causes the

bilayer to compress when cooled and unbind when heated, due to bending modes in the absence of interlamellar contacts37,38,39. Noticeably, the topology of the broken spectrin mesh during

malaria infection of RBCs is somewhat similar to the random polymerization described above1. RBCs experience permanent deformations in the form of echinoytosis either in patients with liver

diseases40 or in patients with Low Density Lipoprotein (LDL) deficiency2 and malaria41. These deformations were interpreted as a consequence of the dissociation of the membrane from the

spectrin mesh. When these cells flow into capillaries, they experience large deformations in the form of plastic flow42. The random break-up of the spectrin mesh could create defects on the

surface of the membranes1, which would cause the deformation to become plastic. Such process can be described using the newly developed model of plastic flow in glassy and amorphous

materials43,44. On the other hand the contour of cancer cells was found to display a fractal behavior that would help identifying cancer cells from normal cells45,46. METHODS We used

polymerizable lipids [1,2-bis(10,12-tricosadiynoyl)-_sn_-glycero-3-phosphocholine] purchased from Avanti Lipids as powder and stored at −20°C. When spherical vesicles made of these lipids

are cooled below , they undergo a first-order type of shape transformation from spherical vesicles to helical ribbons and tubules27. In two-dimensions monolayers of these lipids form spirals

below _T__m_ and a target pattern above _T__m_21,47. The transformation from tubules/ribbons to vesicles when the temperature is increased is also caused by the relaxation of the chiral

torque due to thermal fluctuations48. We prepared the vesicles using the hydration method: A lipid film from a stock solution of 6 mg/ml in chloroform was spread on a concave surface of a

custom-made teflon container and evaporated over night under a stream of nitrogen. We hydrated the lipid film with deuterated methanol:water (Aldrich, Inc.) [75:25 (v:v)] to a lipid

concentration of 3 mg/ml and kept it in an oven at 50°C for several hours to allow the vesicles to swell. This ensured that the vesicles obtained were Giant Unilamellar Vesicles (GUVs). We

heated the vesicles to various temperatures above _T__m_ and the results were not affected. We used the hydration method in conjunction with the water/alcohol mixing to produce GUV

preferably to the electroformation method because we wanted to avoid any electrostatic effects that migh affect the membranes' properties. Since the lipid molecules were not deuterated,

the contrast variation stemmed from the difference between the deuterated solvent and the lipid bilayer. The contrast in the scattering will be between the bilayer and the deuterated water

solution. We cooled the vesicles below T_m_ at a rate of 1°C/hour while we kept them in the dark. We polymerized the lipid molecules by exposing the tubules that were kept at 15°C to a UV

lamp set at 254 nm and with an intensity of 4 μW/cm2. We measured the degree of polymerization as the area under the absorption curve of the polymer using a UV/Vis spectrometer (Genesys

10S)49. For our scattering experiments, we prepared various samples each of which corresponded to a separate experiment or step as illustrated in Figure 3. The control samples, Step I in

Figure 3, included tubules maintained at 15°C ± 0.1°C throughout the scattering experiment in 1-mm-thick quartz cells. We prepared another set of samples by reheating the polymerized

vesicles to 45°C and keeping them in this state for several hours before letting them cool to 15°C when they wrinkled before we started the scattering experiments (Step III). The last set of

samples were similar to the second set except that we heated them to 45°C and performed the scattering experiments at this temperature. This is shown as Step IV in Figure 3. When changing

temperatures, we allowed several hours for the vesicles to equilibrate at the prescribed temperature before we started the data acquisition at the new temperature. The neutron scattering and

data acquisition ran for 12 hours continuously. DATA ANALYSIS AND BACKGROUND CORRECTION The sample's cross section is measured by subtracting the empty cell intensity from the total

intensity. The transmission are computed with respect to an empty beam by using a beam stopper and record electronic background that needs to be subtracted. As seen from the intensity at

high Q (≥0.4) the incoherent scattering is rather flat and this is due to the solid angle correction from geometric distortion. Although the diminution in the transmission through heavy

water is around 3%, which is less than the diminution at high Q due to geometric distortion, this has been corrected with empty cells containing D2O. Because we used thin quartz cells that

are 500 μm thick, multiple scattering was minimized. Substraction of incoherent background which is visible mostly at high _Q_ is performed by empty cell substraction as well as solvent

without structure subtraction. At high _Q_ we plot _I_(_Q_)_Q_−4 versus _Q_. The slope gives the value of incoherent background which is also reduced by using as little hydrogen atoms as

possible. Using a deuterated solvent reduces greatly the incoherent background because of the large differences between the cross section and scattering densities of hydrogen and deuterium

atoms. As seen from all scattering plots, the incoherent scattering (at high _Q_) is almost flat. CHANGE HISTORY * _ 10 DECEMBER 2014 A correction has been published and is appended to both

the HTML and PDF versions of this paper. The error has not been fixed in the paper. _ REFERENCES * Gov, N. & Safran, S. Red blood cell membrane fluctuations and shape controlled by

ATP-Induced cytoskeletal defects. Biophysical Journal 88, 1859–1874 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Lange, Y. & Steck, T. L. Mechanism of red blood cell

acanthocytosis and echinocytosis in vivo. J. Membr. Biol. 77, 153–159 (1984). Article  CAS  PubMed  Google Scholar  * Canham, P. B. The minimum energy of bending as a possible explanation of

the biconcave shape of the human red blood cell. J. Theor. Biol. 26, 61–81 (1970). Article  CAS  PubMed  Google Scholar  * Helfrich, W. Elastic properties of lipid bilayers: theory and

possible experiments. Z Naturforsch C 28, 693–703 (1973). Article  CAS  PubMed  Google Scholar  * Hill, R. The Mathematical Theory of Plasticity (Oxford University Press, 1998). * Robertson,

R. E. Theory for the plasticity of glassy polymers. J. Chem. Phys. 44, 3950–3956 (2004). Article  ADS  Google Scholar  * Witten, T. A. Stress focusing in elastic sheets. Rev. Mod. Phys. 79,

643–675 (2007). Article  ADS  MathSciNet  MATH  Google Scholar  * Cerda, E., Chaieb, S., Melo, F. & Mahadevan, L. Conical dislocations in crumpling. Nature 401, 46–49 (1999). Article 

ADS  CAS  Google Scholar  * Chaieb, S. & Melo, F. Crescent singularities and stress focusing in a buckled thin sheet: mechanics of developable cones. Phys. Rev. E Stat Phys Plasmas

Fluids Relat Interdiscip Topics 60, 6091–6103 (1999). CAS  PubMed  Google Scholar  * Mora, T. & Boudaoud, A. Thin elastic plates: On the core of developable cones. EPL 59, 41–47 (2002).

Article  ADS  CAS  Google Scholar  * Sultan, E. & Boudaoud, A. Statistics of crumpled paper. Phys. Rev. Lett. 96, 136103–136106 (2006). Article  ADS  CAS  PubMed  Google Scholar  *

Vliegenthart, G. A. & Gompper, G. Forced crumpling of self-avoiding elastic sheets. Nat. Mater. 5, 216–221 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Flory, P. J. Principles of

Polymer Chemistry (Cornell University Press, 1953). * Kantor, Y., Kardar, M. & Nelson, D. R. Tethered surfaces: Statics and dynamics. Phys. Rev. A 35, 3056–3071 (1987). Article  ADS 

MathSciNet  CAS  Google Scholar  * Gomes, M. a. F. Paper crushes fractally. J. Phys. A: Math. Gen. 20, L283–L284 (1987). Article  ADS  Google Scholar  * Plourabou, F. & Roux, S.

Experimental study of the roughness of crumpled surfaces. Physica A: Statistical Mechanics and its Applications 227, 173–182 (1996). Article  ADS  Google Scholar  * Balankin, A. S., Silva,

I. C., Martnez, O. A. & Huerta, O. S. Scaling properties of randomly folded plastic sheets. Phys. Rev. E 75, 051117–051119 (2007). Article  ADS  CAS  Google Scholar  * Wen, X. et al.

Crumpled and collapsed conformation in graphite oxide membranes. Nature 355, 426–428 (1992). Article  ADS  CAS  Google Scholar  * Spector, M. S., Naranjo, E., Chiruvolu, S. &

Zasadzinski, J. A. Conformations of a tethered membrane: Crumpling in graphitic oxide? Phys. Rev. Lett. 73, 2867–2870 (1994). Article  ADS  CAS  PubMed  Google Scholar  * Mutz & Brienne

Wrinkling transition in partially polymerized vesicles. Phys. Rev. Lett. 67, 923–926 (1991). Article  ADS  CAS  PubMed  Google Scholar  * Chaieb, S., Natrajan, V. K. & El-rahman, A. A.

Glassy conformations in wrinkled membranes. Phys. Rev. Lett. 96, 078101–078106 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Martin, J. E. & Hurd, A. J. Scattering from fractals.

J. Appl. Cryst. 20, 61–78 (1987). Article  CAS  Google Scholar  * Teixeira, J. Small-angle scattering by fractal systems. J. Appl. Cryst. 21, 781–785 (1988). Article  Google Scholar  * Bale,

H. D. & Schmidt, P. W. Small-angle x-ray-scattering investigation of submicroscopic porosity with fractal properties. Phys. Rev. Lett. 53, 596–599 (1984). Article  ADS  CAS  Google

Scholar  * Hammouda, B. A new GuinierPorod model. J. Appl. Cryst. 43, 716–719 (2010). Article  CAS  Google Scholar  * Kratky, O. & Porod, G. Diffuse small-angle scattering of x-rays in

colloid systems. J. Colloid. Sci. 4, 35–70 (1949). Article  CAS  PubMed  Google Scholar  * Thomas, B. N., Safinya, C. R., Plano, R. J. & Clark, N. A. Lipid tubule self-assembly: Length

dependence on cooling rate through a first-order phase transition. Science 267, 1635–1638 (1995). Article  ADS  CAS  PubMed  Google Scholar  * Schmidt, C. F. et al. Existence of a flat phase

in red cell membrane skeletons. Science 259, 952–955 (1993). Article  ADS  CAS  PubMed  Google Scholar  * Abraham, F. F. & Nelson, D. R. Diffraction from polymerized membranes. Science

249, 393–397 (1990). Article  ADS  CAS  PubMed  Google Scholar  * Tallinen, T., strm, J. A. & Timonen, J. The effect of plasticity in crumpling of thin sheets. Nat. Mater. 8, 25–29

(2009). Article  ADS  CAS  PubMed  Google Scholar  * Attal, R., Chaieb, S. & Bensimon, D. Breaking of replica symmetry in a mean-field model of disordered membranes. Phys. Rev. E 48,

2232–2239 (1993). Article  ADS  CAS  Google Scholar  * Nelson, D. R. & Radzihovsky, L. Grain-boundary instabilities and buckling in partially polymerized membranes. Phys. Rev. A 46,

7474–7479 (1992). Article  ADS  CAS  PubMed  Google Scholar  * Bouchaud, E., Lapasset, G. & Plans, J. Fractal dimension of fractured surfaces: A universal value? EPL 13, 73–79 (1990).

Article  ADS  CAS  Google Scholar  * Gennes, P.-G. d. Scaling Concepts in Polymer Physics (Cornell University Press, 1979). * Sachdev, S. & Nelson, D. R. Crystalline and fluid order on a

random topography. J. Phys. C: Solid State Phys. 17, 5473–5489 (1984). Article  ADS  Google Scholar  * Als-Nielsen, J. et al. Observation of algebraic decay of positional order in a smectic

liquid crystal. Phys. Rev. B 22, 312–320 (1980). Article  ADS  CAS  Google Scholar  * Lipowsky, R. & Leibler, S. Unbinding transitions of interacting membranes. Phys. Rev. Lett. 56,

2541–2544 (1986). Article  ADS  CAS  PubMed  Google Scholar  * Wennerstroem, H. The unbinding transition and lamellar phase-lamellar phase coexistence. Langmuir 6, 834–838 (1990). Article 

CAS  Google Scholar  * Abraham, F. F. & Kardar, M. Folding and unbinding transitions in tethered membranes. Science 252, 419–422 (1991). Article  ADS  CAS  PubMed  Google Scholar  *

Owen, J. S. et al. Erythrocyte echinocytosis in liver disease. role of abnormal plasma high density lipoproteins. J Clin Invest 76, 2275–2285 (1985). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Bessis, M. Living blood cells and their ultrastructure (Springer-Verlag (Berlin and New York) 1973). * Li, J., Lykotrafitis, G., Dao, M. & Suresh, S. Cytoskeletal

dynamics of human erythrocyte. PNAS 104, 4937–4942 (2007). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Langer, J. S. Shear-transformation-zone theory of plastic deformation

near the glass transition. Phys. Rev. E 77, 021502–021515 (2008). Article  ADS  CAS  Google Scholar  * Marchenko, V. I. & Misbah, C. Model of plasticity of amorphous materials. Phys.

Rev. E 84, 021502–021508 (2011). Article  ADS  CAS  Google Scholar  * Esgiar, A., Naguib, R. N. G., Sharif, B., Bennett, M. & Murray, A. Fractal analysis in the detection of colonic

cancer images. IEEE Transactions on Information Technology in Biomedicine 6, 54–58 (2002). Article  PubMed  Google Scholar  * Klein, K., Maier, T., Hirschfeld-Warneken, V. C. & Spatz, J.

P. Marker-free phenotyping of tumor cells by fractal analysis of reflection interference contrast microscopy images. Nano Lett. 13, 5474–5479 (2013). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Basnet, P. B., Mandal, P., Malcolm, D. W., Mann, E. K. & Chaieb, S. Chiral hierarchical self-assembly in langmuir monolayers of diacetylenic lipids. Soft

Matter 9, 1437–1446 (2013). Article  ADS  CAS  Google Scholar  * Selinger, J. V., MacKintosh, F. C. & Schnur, J. M. Theory of cylindrical tubules and helical ribbons of chiral lipid

membranes. Phys. Rev. E 53, 3804–3818 (1996). Article  ADS  CAS  Google Scholar  * Regen, S. L., Czech, B. & Singh, A. Polymerized vesicles. J. Am. Chem. Soc. 102, 6638–6640 (1980).

Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS We would like to thank Jyotsana Lal for her help and Elizabeth K. Mann for critical reading of the manuscript. We also

thank King Abdullah University of Science and Technology (KAUST) for financial support. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Division of Physical Science and Engineering, King

Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, KSA Sahraoui Chaieb Authors * Sahraoui Chaieb View author publications You can also search for this author inPubMed

 Google Scholar CONTRIBUTIONS S.C. performed the analyses discussed the results and wrote the manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The author declares no competing financial

interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit

http://creativecommons.org/licenses/by-nc-sa/3.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Chaieb, S. Elasto-plasticity in wrinkled polymerized lipid membranes. _Sci

Rep_ 4, 3699 (2014). https://doi.org/10.1038/srep03699 Download citation * Received: 23 September 2013 * Accepted: 16 December 2013 * Published: 15 January 2014 * DOI:

https://doi.org/10.1038/srep03699 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently

available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative